如何防止过拟合和欠拟合

如何防止过拟合和欠拟合

过拟合（Over-Fitting）

高方差

在训练集上误差小，但在测试集上误差大，我们将这种情况称为高方差（high variance），也叫过拟合。

欠拟合（Under-Fitting）

在训练集上训练效果不好（测试集上也不好），准确率不高，我们将这种情况称为高偏差（high bias），也叫欠拟合。

过拟合解决方法：

其直观的表现如下图所示，随着训练过程的进行，模型复杂度增加，在training data上的error渐渐减小，但是在验证集上的error却反而渐渐增大——因为训练出来的网络过拟合了训练集, 对训练集外的数据却不work, 这称之为泛化(generalization)性能不好。泛化性能是训练的效果评价中的首要目标，没有良好的泛化，就等于南辕北辙, 一切都是无用功。
过拟合是泛化的反面，好比乡下快活的刘姥姥进了大观园会各种不适应，但受过良好教育的林黛玉进贾府就不会大惊小怪。实际训练中, 降低过拟合的办法一般如下：

• 正则化(Regularization)

L2正则化：目标函数中增加所有权重w参数的平方之和, 逼迫所有w尽可能趋向零但不为零. 因为过拟合的时候, 拟合函数需要顾忌每一个点, 最终形成的拟合函数波动很大, 在某些很小的区间里, 函数值的变化很剧烈, 也就是某些w非常大. 为此, L2正则化的加入就惩罚了权重变大的趋势.

L1正则化：目标函数中增加所有权重w参数的绝对值之和, 逼迫更多w为零(也就是变稀疏. L2因为其导数也趋0, 奔向零的速度不如L1给力了).大家对稀疏规则化趋之若鹜的一个关键原因在于它能实现特征的自动选择。一般来说，xi的大部分元素（也就是特征）都是和最终的输出yi没有关系或者不提供任何信息的，在最小化目标函数的时候考虑xi这些额外的特征，虽然可以获得更小的训练误差，但在预测新的样本时，这些没用的特征权重反而会被考虑，从而干扰了对正确yi的预测。稀疏规则化算子的引入就是为了完成特征自动选择的光荣使命，它会学习地去掉这些无用的特征，也就是把这些特征对应的权重置为0。

• 随机失活(dropout)

在训练的运行的时候，让神经元以超参数p的概率被激活(也就是1-p的概率被设置为0), 每个w因此随机参与, 使得任意w都不是不可或缺的, 效果类似于数量巨大的模型集成。

• 逐层归一化(batch normalization)

这个方法给每层的输出都做一次归一化(网络上相当于加了一个线性变换层), 使得下一层的输入接近高斯分布. 这个方法相当于下一层的w训练时避免了其输入以偏概全, 因而泛化效果非常好.

• 提前终止(early stopping)

理论上可能的局部极小值数量随参数的数量呈指数增长, 到达某个精确的最小值是不良泛化的一个来源. 实践表明, 追求细粒度极小值具有较高的泛化误差。这是直观的，因为我们通常会希望我们的误差函数是平滑的, 精确的最小值处所见相应误差曲面具有高度不规则性, 而我们的泛化要求减少精确度去获得平滑最小值, 所以很多训练方法都提出了提前终止策略.
典型的方法是根据交叉叉验证提前终止: 若每次训练前, 将训练数据划分为若干份, 取一份为测试集, 其他为训练集, 每次训练完立即拿此次选中的测试集自测. 因为每份都有一次机会当测试集, 所以此方法称之为交叉验证. 交叉验证的错误率最小时可以认为泛化性能最好, 这时候训练错误率虽然还在继续下降, 但也得终止继续训练了.

• Bagging

集成学习Bagging使模型更加的稳定，其作用是因为降低了模型的方差，对过拟合有一定的作用

欠拟合解决方法：

• 添加其他特征项，模型出现欠拟合的时候是因为特征项不够导致的，可以添加其他特征项来很好地解决，例如，“组合”、“泛化”、“相关性”三类特征是特征添加的重要手段，无论在什么场景，都可以照葫芦画瓢，总会得到意想不到的效果。除上面的特征之外，“上下文特征”、“平台特征”等等，都可以作为特征添加的首选项。

• 为了提高复杂关系的拟合能力， 在特征工程中经常会把一阶离散特征两两组合， 构成高阶组合特征。 以广告点击预估问题为例， 原始数据有语言和类型两种
  离散特征， 表1.2是语言和类型对点击的影响。 为了提高拟合能力， 语言和类型可
  以组成二阶特征， 表1.3是语言和类型的组合特征对点击的影响。

但是在很多实际问题中， 我们常常需要面对多种高维特征。 如果简单地两两
组合， 依然容易存在参数过多、 过拟合等问题， 而且并不是所有的特征组合都是
有意义的。 因此， 需要一种有效的方法来帮助我们找到应该对哪些特征进行组
合。

本节介绍一种基于决策树的特征组合寻找方法[1]（关于决策树的详细内容可见
第3章第3节） 。 以点击预测问题为例， 假设原始输入特征包含年龄、 性别、 用户
类型（试用期、 付费） 、 物品类型（护肤、 食品等） 4个方面的信息， 并且根据原
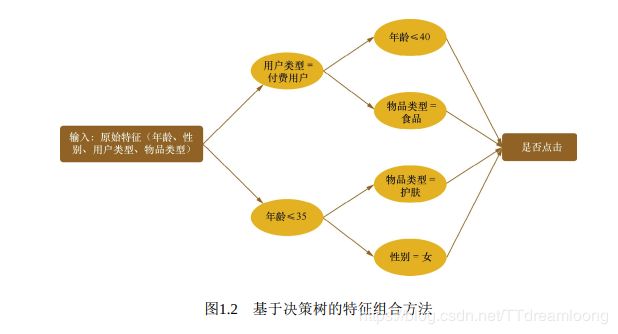
始输入和标签（点击/未点击） 构造出了决策树， 如图1.2所示。
于是， 每一条从根节点到叶节点的路径都可以看成一种特征组合的方式。 具
体来说， 就有以下4种特征组合的方式。
（1） “年龄<=35”且“性别=女”。
（2） “年龄<=35”且“物品类别=护肤”。
（3） “用户类型=付费”且“物品类型=食品”。
（4） “用户类型=付费”且“年龄<=40”。

（详见百面机器学习）

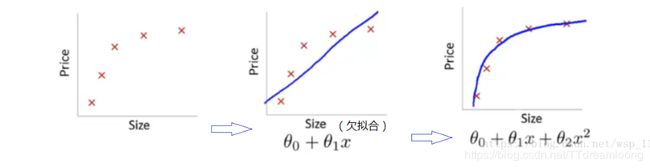
添加多项式特征，例如将线性模型通过添加二次项或者三次项使模型泛化能力更强。

减少正则化参数，正则化的目的是用来防止过拟合的，当模型出现了欠拟合，则需要减少正则化参数。

导致欠拟合的主要原因，模型的复杂度不够，增加模型的复杂度来提高模型的拟合能力，添加卷积层，去除Dropout、减小正则化参数等

如何判断欠拟合、适度拟合、过拟合

1.欠拟合：

假定训练集误差是 15%，验证集误差是16%。这样则说明算法并没有在训练集中得到很好的训练，如果训练集数据的拟合度不高，就是数据欠拟合，就可以说这种算法偏差比较高。也就是我们说的没有训练好。
相反，它对于验证集产生的结果是合理的，验证集中的错误率只比训练集的多了1%，所以这种算法偏差高，因为它甚至不能拟合训练集。就更别提验证集了。

训练集和验证集的误差都较高，但相差很少——>欠拟合

2.适度拟合

训练集误差是 0.5%，验证集误差是 1%，这样的结果偏差和方差都很低，说明训练效果很好，这是我们想要的结果。

训练集和验证集的误差都很低——>适度拟合

3.过拟合

假定训练集的误差是 1%，验证集误差是 11%，可以看出训练集训练的非常好，而验证集很差，从而可以判断可能过度拟合了训练集，在某种程度上，验证集并没有充分利用交叉验证集的作用，这就是过拟合现象，也称为“高方差”。

训练集误差较低，验证集误差比训练集大较多——>过拟合

4.最差的情况

训练集误差是 15%，偏差相当高，但是，验证集的评估结果更糟糕，错误率达到 30%，这样说明算法偏差高，因为它在训练集上结果不理想，而且方差也很高，这是方差偏差都很糟糕的情况。这是我们最不想看到的情况。

个人Github链接