机器学习-神经元网络

比较人脑和电脑

主要应用领域

1.分类和模式识别
诊断，声音识别，文字识别
2.回归/拟合
3.模型完善(Mustervervollständigung)
。。。

Perceptron

基本思想

模仿现实生活中动物的感知和反应原理

图中左边为从眼睛捕捉到事物到形成反应方案的过程。右边为对这个过程的模仿。

建立一个Perceptron

其中W为权值，o为输出X为输入向量，
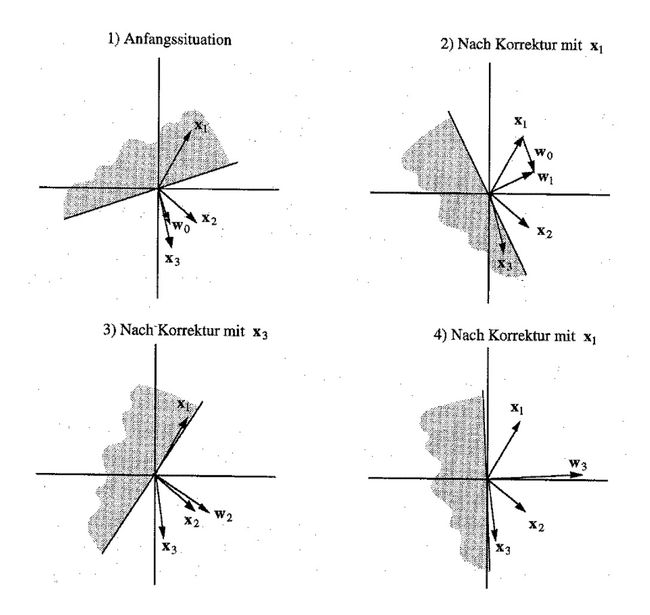
Perceptron的学习过程是不断调整他的权值W，他的目标是找到最佳的超平面，通过这个超平面可以很好的对数据进行分类，使得处于超平面不同侧的数据在目标属性上具有不同的属性值。比如正负值问题，得到的对应的超平面应该能够使其一侧的值为正，而另一侧的为负。下图展示了正负问题的学习过程，原问题为一维问题，我们通过引入 x0 进行增维。初始W随机，X为训练数据。W为权值向量

对应的学习算法为：

start: 获得训练数据集P，N
       随机初始化权值向量w(0)
       t=0 
Test：从P或N中随机选出一个点x
          if(x in P && w(t)x>0) goto Test
          if(x in P && w(t)x<0) goto Add
          if(x in N && w(t)x<0) goto Test
          if(x in N && w(t)x>0) goto Sub
Add:w(t+1)=w(t)+x
    t=t+1
    goto Test
Sub:w(t+1)=w(t)-x
    t=t+1
    goto Test

//注意要分正项错判和负项错判两种情况
//一般情况下，一w向量的方向为正，反方向为负

多层向前反馈神经元网络(Multi Layer Feedforward Neural Network)

纲要

动机：
Perceptron的局限性，比如他解决不了异或问题。
构建MLNN：
反响传播(Backpropagation)
构建RBF网络：
神经元
学习
问题及优化：

感知器(Perceptron)的局限性

问题：
当|w|>>|x|时，学习过程将十分缓慢。
对策：标准化
最糟糕的情况：
训练数据几乎反向平行，这是学习到死的节奏
对策是梯度下降-Delta规则

梯度下降

误差函数

E(w⃗ )=12|D|∑d∈D(td−od)2

其中t为目标值，o输出值
我们学习的目标就是使误差函数最小化
梯度：

ΔE(w)≡[∂E∂w0,...,∂E∂wn]

根据梯度我们进行权值调整

w⃗ =w⃗ +Δw⃗ Δw⃗ =−ηΔE(w⃗ )

或者：

wi=wi+ΔwiΔwi=−η∂E∂wi

梯度下降-Delta规则

∂E∂wi≅i∂∂wi12∑d∈D(td−od)2=12∑d∈Di∂∂wi(td−od)2=12∑d∈D2(td−od)i∂∂wi(td−od)=∑d∈D(td−od)i∂∂wi(td−w⃗ x⃗ )(注这里的激活函数必须是可微的，比如o(x⃗ )=∑w⃗ x⃗ )∂E∂wi≅∑d∈D(td−od)(−xid)Δwi=η∑d∈D(td−od)(xid)

//算着算着就把1/|D|扔了？？？这样不是|D|越大abstieg越大吗？？虽然方向没有变就是了

Kernel方法

单独使用一个Perceptron无法实现XOR问题，但是通过Kernel方法我们可以实现这种功能
我么如下定义我们的Kernel：
已知两个向量 x⃗ ,y⃗  ,和相应到另一个空间的转换函数 ϕ 。那么我们定义kernel为：

K(x⃗ ,y⃗ )=<ϕ(x⃗ ),ϕ(y⃗ )>

//为什么非得有两个向量呢？？？有差吗？？？
//注意所谓核方法并不是指输入空间的转化。 ϕ 为映射函数，尖括号表示内积，核技巧的思想是，在学习和预测中只定义核函数K，而不显式的定义映射函数 ϕ 。通常直接计算K比较容易，而通过 ϕ 计算K比较难。
通过这种方法我们把原始空间中相对复杂的问题转化到另外一个空间并通过相对简单的方法来解决问题。

如图转换空间中的一个简单的分界直线对应着原始空间中的一条复杂的分界线
对应的在转换空间中的学习可以表示为：

wt+1→=wt→+yiϕ(xi→)⇒wt→=∑i=1lαiyiϕ(xi→)

//后半截看不懂？？l是错分的实例的个数， α 为调整参数？？
Kernel Perceptron算法：

//这个算法又看没懂，特别是中间的那个if语句，天啊，他究竟想表达什么？？？
//好像还是可以理解的，第一个等号可以理解为赋值，所以这句话就是说如果sign不等于y就执行(注意y其实表示的是符号，正负一啊)，接下来看第二个式子，K表示转换后的内积，所以直接代入，前半部分前面刚刚提过，就是 wj 了，再点乘后半部分，就是感知器的输出了
//不知为何都不用激活函数了??
//另外 α 初始为0，那么sign(0)应该怎么算？？如果为正，那是不是说在遇见第一个y为负之前碰到的数据都是白搭的？？
//这里可以看出l并不是指错分的个数， α 才是。那么这里 wj 的算法就存在问题了，因为只有错分的时候才需要调整w啊？？
//好像理解错了 α 向量和实例向量是不一样的，他就是表示有l个 α 他对应的是实例，而不是实例的维度。程序就是遍历一下实例，把其中错分的给标出来，然后求出对应的输出函数。但是 α 初始为0，还是觉得是个问题？？
//这个算法的主要意义在于在不明确指出映射函数得条件下，得出对应的输出函数
//这个算法并没有使用梯度下降，是因为不知道对应的 Od 吗？？因为要知道他的话就非得知道对应的映射函数不可？？

构建MLNN

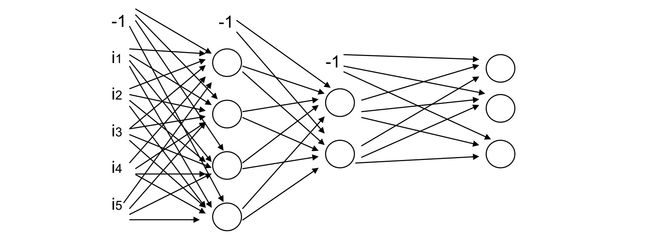
构建一个MLNN一般要考虑下面三个问题：
1.构建网络：
MLNN含有一个或多个中间层或叫覆盖层
2.学习方法：
一般化的delta规则：向后传播
3.构建神经元：
区别于前面的这里一般使用的是非线性的激活函数

构建神经元

先看一下他长什么样子

//插图的家伙偷懒了，没把j加进去，还好下面的解释有提到
其实基本上了上面一样，只要知道j表示的是神经元的编号就是了。
xij 表示j号神经元的第i个输入。
wij 有点特殊，他表示神经元i和神经元j之间的权值。但想想好像也不是那么特殊。
outputs是输出神经元的集合
Downstream(j)表示神经元j的直接后继
//感觉 xij 应该解释为，神经元j从神经元i获得的输入。和原解释存在很大的区别，往下看看在做讨论？？

激活函数

非线性激活函数并不唯一，常用的有下面两种：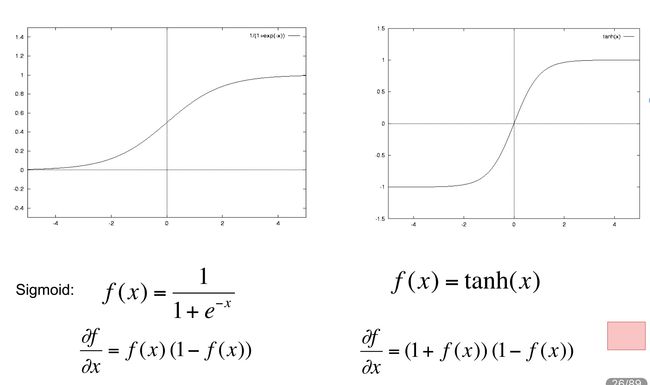
其中tanh为双曲函数：

tanh(x)=ex−e−xex+e−x

Backpropagation Algorithmus

已知：
1.训练数据集（input/output）
2.学习速率 η
3.Netztopologie网络拓扑结构：
中间层的数目，且层之间是单向向前全射(有全射这东西吗？？)
(Anzahl und Ausmaße der Zwischenschichten.Schichten sind vorwärts gerichtet verbunden)
学习目标：
寻找合适的W，使得针对每个T中的input得到的结果和T中的output相匹配。
学习方法：
梯度下降法 → 一般化的Delta规则

1.用小的随机值来初始化权值
2.repeat：
    选出一组训练数据d
    获得输出值
    计算输出误差
    向后逐步算出误差在每个神经元的传播值：Delta_j
    调整每个神经元的权值

其中：

δj={oj(1−oj)∑k∈Downstream(j)δkwjkoj(1−oj)(tj−oj)j∉outputj∈output

而每个神经元的权值的调整值为：

Δwij=ηδjxij

梯度下降-一般化的Delta规则

误差函数：

Ed(x⃗ ≡12∑k∈outputs(tk−ok)2)

按梯度方向的权值改变：//加负号是因为要下降而非要上升

Δwij=−η∂Ed∂wij

而根据链接规则我们有：

∂Ed∂wij=∂Ed∂netj∂netj∂wij=∂Ed∂netjxij

同理可得：

∂Ed∂netj=∂Ed∂oj∂oj∂netj

其中有：

∂Ed∂oj=∂∂oj12∑k∈output(tk−ok)2=−(tj−oj)∂oj∂netj=∂f(netj)∂netj=oj(1−oj)

上面是输出节点的情况，现在来看一下中间层的节点的情况：
//输出节点和中间层节点的主要区别在于，每个输出节点对应一个额定值，而一个中间层的节点他可从下一层的所有节点获得反馈。另外他并没有明确的E定义

因此可以得到

Δwij=−η∂Ed∂wijΔwij=ηδjxijδj={oj(1−oj)∑k∈Downstream(j)δkwjkoj(1−oj)(tj−oj)j∉outputj∈output

构建RBF网络

RBF

RBF即radiale Basisfunktion，他是一个实数方程(reelle Funktion)，他的值只和到起点的距离有关，即 φ(x)=φ(||x||) 。之所以叫这个名字是因为他是放射性对称的(radialsymmetrisch),并且它经常被用做拟合的基本方程(als Basisfuntionen einer Approximation)。
一般化的我们将RBF表示为： φ(x,c)=φ(||x−c||)
RBF有很多种，下面会用到的应该是:高斯RBF: e−(ar)2

RBF网络

RBF网络是Radial Basis Function网络的缩写 。他具有如下结构：
1.向前单向网络
2.由三层组成，分别是输入层，隐藏层(中间层)和输出层
3.Neuronen des hidden layer:lokale rezeptie Felder？？只有在激活函数附近的点才回被分类,他以 μ 为中心(Zentrum/Mittelwert)，以 σ 为影响范围(Reichweite/std. abweichung)。
这个激活函数是一个放射性对称的基本函数(radialsymmetrische Basisfunktionen): hi(||X−Xi||) Xi 表示对应神经元的中心向量，即上面提到的 μ 。X表示输入向量。
4.输出层的神经元的 输出为：

oj=∑i∈hiddenoiwij    j∈output

//不用激活函数了吗？？？？
//完全看不出有什么好的？？？

优化RBF网络

中间层：
给输入的维度加入一个权值，使各维度不对称(gewichtete Eingabediemensioinen →unsymmetrischeFelder )
总之就是把原来对称的结构，改成非对称的

oi(x⃗ )=e−∑kξk(xk−μik)22σ2i

输出层：
则是把输出进行标准化：

oj=∑ioiwij∑ioi

//但为什么是除以对应神经元的输入呢？？？

RBF网络的学习算法

还是BackProp：并通过梯度下降调整
范围中心：

∂E∂μji=∑n∑k(ok(xn)−tnk)wkjexp(−||xn−μj||22σ2j)||xn−μji||σ2j

范围：

∂E∂σj=∑n∑k(ok(xn)−tnk)wkjexp(−||xn−μj||22σ2j)||xn−μj||2σ3j

//完全不知道这是在干嘛，式子了看不懂，这n究竟是啥？？？应该不是表示n次方吧？？
Gewichte der Ausgabeschicht????

BackProp的缺点

1.非线性：高计算量
2.局部最小
3.激活函数的范围可以非常大：//keine lokalen Felder ????
//其实三个都没懂？？？
/*这是一个建议，没懂？？？？
Hybride Lernverfahren(als Idee)
Finden lokaler Felder:Zentrum und/oder Reichweite-unüberwacht,d.h. z.B. ohne die Sollausgabe zu betrachten(oder durch andere Verfahren)
Anpassen der übrigen Gewichte ÖAusgabeschicht-durch Gradientenabstieg
*/

问题及改善

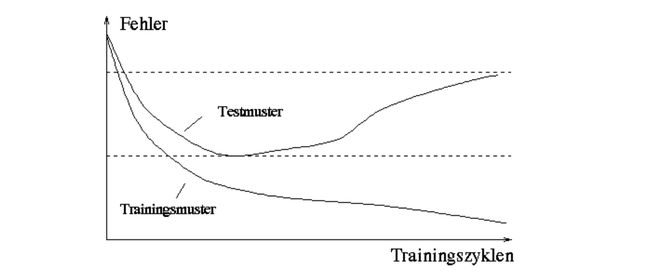
梯度下降存在的问题

上图显示了学习过程中的几种常见的问题，其中E表示误差，w表示权值。
学习的过程就是通过调整w即权值不断降低误差E的过程，他依赖于下面几个元素：
1.误差面的坡度//也就是梯度了
2.出现局部最小
3.Ausprägung der lok.Min.//不知要表达啥？？？
4.Lernrate//太大了收敛不了
/*这里举例讲了几个问题，没懂？？？
Linear fit → Fehlerkurve,Lernen
Too large → Lernrate zu groß, keine Konverganz
Undetermined problem → Großes Tal,kein Minimum
*/

优化梯度下降

1.惰性变量(trägheitsterm,Momentum)
通过引入惰性变量 α 和上次权值的改变量，使得当前的权值改变不仅受梯度的影响，而且还受上一回改变的大小的影响。通过这种方法可以有效的解决上图中右上和右下方的图像中出现的问题(flache Plateau,steilen Schluchten)。新的改变量表示为：

Δwij(t)=ηδj(t)xij(t)+αΔwij(t−1)

其中 α∈[0.2,0.9]
2.标准化步幅(Normierung der Schrittweite)

Δwij=ηsign(δj)xij         (Manhattan−Training)

3.调整学习速率
通过梯度比较调整学习速率：（RPROP：Resilient Propagation）

{η(t+1)>η(t)η(t+1)<η(t)when sign(∂E∂w(t+1))=sign(∂E∂w(t))other

误差函数：

E=12∑i∈outputs(ti−oi)2

权值调整：

Δwij=⎧⎩⎨⎪⎪⎪⎪−Δij(t)+Δij(t)0when∂E∂wij(t)>0when∂E∂wij(t)<0other

学习速率依赖于梯度比较：

Δij=⎧⎩⎨⎪⎪⎪⎪Δij(t−1)η+Δij(t−1)η−Δij(t−1)when∂E∂wij(t−1)∂E∂wij(t)>0when∂E∂wij(t−1)∂E∂wij(t)<0other

其中 η+>1,η−<1
\这里并没有使用梯度下降，而只是求偏导。小于零表示单调下降，故应该加。大于零表示单调上升，故应该减。

MLNN拓扑结构的选择

层的数量 ↔ 激活函数：
激活函数应该和层数相匹配，
比如，当只有三层的时候，对应的激活函数建议用sigmoid函数，当然也可以使用其他的函数，但还是建议使用下面两类函数：
1.任意的布尔函数
2.任意的连续函数
对于四层的情况，使用sigmoid函数也是极好的，当如果要用其他函数，好吧还真没有什么限制
/*不理解为什么，写着3层对应sigmoid，然后又写可以是任意布尔函数或连续函数？？？？？？？？？？？？？？？？？？？
3 Layer(1 hidden Layer-sigmoid):
.jede Boolsche Funktion abbildbar
.jede kontinuierliche baschränkte Funktion
4 Layer(2 hidden Layer -sigmoid)
.beliebige Funktionen mit beliebiger Genauigkeit
schon eine geringe Tiefe ist ausreichend
Lernverhalten-Topologieauswahl
Anzahl der Neuronen pro Schicht im Bezug zu der Anzahl von(stochastisch unabhängigen)Lerndaten ist wichtig
-allgemeine Aussage zur Topologie nicht möglich
Topologie ↔ Kapazität(VC-Dimension)
Beispiel:
gestrichelte Kurve
soll eingelernt werden
*/
另外在确定神经元的数量之前，最后还要考虑一下，训练数据集的大小。如果训练数据不足，最好还是不要有太多的神经元比较好。

优化MLNN的构建(Verbesserung der Generalisierung(~realer Fehler) von MLNN)

目标：在训练NN的同时，优化他的拓扑结构
由于大小问题可能导致的问题//为什么不直接叫大小呢，难道还有区别？？？
(Anpassung der Kapazität)
1.网络过大可能导致背诵数据//什么意思，没懂？？？？
2.扩展过小的网络知道能够学习数据//还是没懂？？？？
缩减的方法(Methoden der Reduzierung)
Weight Decay, Weight Elimination:
根据w的大小，加入额外的惩罚。
//前面的英语不知道是什么意思？？？

E(w)=ED(w)+12λ∑w2

//现在时w的大小影响了E，但也没说什么时候适合扩大缩小？？
Optimal Brain Damage:
学习+删除一些连接
(Lernen+anschließend Löschen von Verbindungen)
比如：Taylor序列(Taylor-Entwicklung)
主要思想是：
1.通过剪枝实现瘦身
2.cost function同时又训练错误和网络复杂度决定，这个有多种方法，比如上面提到的泰勒序列等等
OBD的流程：
1.选择一个合理的神经元网络结构
2.训练知道误差最小
3.计算每个神经元的hessian矩阵(确切的说是该矩阵的对角线数据 hkk )
4.计算每个神经元的saliencies： sk=hkku2k/2
5.对结果进行排序，然后减掉几个最小的神经元
6.跳到第2步，重复上述操作
其中 uk 来自perturbation集。
//好吧，数学底子有点差，还得回去看看？？？？
上面就说了个大概，有兴趣的可以看看这个文档
Optimal Brain Damage.pdf
上面都是关于如何瘦身的，现在来看一下增肥的方法。
Cascade Correlation:
优势在于：使NN的大小根据问题进行调整
他的步骤如下：
1.针对问题构建一个最小的NN。也就是只有输入神经元和输出神经元组成的网络。
2.进行训练，直到误差函数最小或无明显优化
3.往中间层加入一个神经元使得，该神经元的输入是输入层每个神经元的输出加上前面已近假如的神经元的输出。使该神经元的输出暂时不加入网络。我们称这个神经元为候选单元(Candidate Unit)
4.对新加入的神经元进行训练，我们的目标是使得 Sj 最大。其中 Sj 是候选单元的输出和输出层输出误差之间的协方差的总和。他可以表示为：

Sj=∑k|∑p(opj−oj−)(δpk−δk−)|

其中k是输出层神经元的索引，p是训练数据的索引，头上带杠的都表示平均值。
同样的我们利用梯度下降的方法进行训练，不过我们这里求的应该是 Sj 的偏导：

δSjδwij=∑k∑pσk∗f′act(netpj)opi(δpk−δk−)

其中：

σk=sign[∑p(opj−oj−)(δpk−δk−)]opj=fact(netpj)

5.现在冻结候选单元的权值，然后使它的输出和所有的输出层的神经元进行连接
6.然后再次重新训练输出层的权值，重复上面的操作，直到误差达到期望。
图片来自wiki。上方两节点表示输出，左侧4节点表示输入。

Dynamc Decay Adjustment-DDA

DDA是用于构建NN分类器的RBF-Topologie：
1.输入层的神经元数量对应着输入空间的维度
2.中间层包含着RBF单元，这些单元会在训练过程中逐渐加入。并且每个单元的输入都对应着输入层每个神经元的输出(单元就是神经元的意思，有点写晕了)
3.输出层的每一个神经元对应这分类器的一个类。
DDA和普通的MLP(多层感知器Multi Layer Perceptrons)的主要区别在于激活函数和中间层的传播规则(propagation rule):
RBF使用小范围的(localized function)radial Gaussians作为激活函数。另外他还用到一个独立参考点得欧几里距离替代MLP中使用的标量积：//这点就是MLP中的权值吧？?？

Ri(x⃗ )=exp(−||x⃗ −ri→||2σ2i)

σ 表示标准差(standard deviation)//怎么来的？？
输出层计算每个类的对应的输出：

f(x⃗ )=∑i=1mAi∗Ri(x⃗ )

m表示针对该类的所有RBF的数量。 Ai 表示这些RBF对应的权值。

DDA就长这个样子
每个中间层的神经元的输入对应的权值向量表示一个高斯分布的中心。当输入向量离一个中间层的神经元的中心点近时，该神经元对应的激活函数的结果就比较大，与之相反如果离得越远则输出越小。每个输出层的神经元只是对对应的RBF进行加权求和。
另外在RBF上还定义了两个阀值 θ+ 和 θ− ,他们需要被手动设定。他们被用来定义一个冲突区域，在这个区域内不允许有属于其他类的RBF的中心出现。

DDA-算法：
假设只有AB两个类, nAj 是属于A类的神经元， jA 表示属于A类的神经元的数量

∀x⃗ ∈训练数据(oBdAx⃗ ∈A) do
if ∃nAi:oAi(x⃗ )>=θpos
      wAi+=1.0
else 建立新的节点 nAjA+1
    μ⃗ =x⃗ 
    σAjA+1=max{σ|∀B≠A,1<=k<=jB:oAjA+1(μk→B)<θneg}
    wAjA+1=1.0
    ∀B≠A∧1<=k<=jB:σBk=max{σ|oBk(x⃗ )<θneg}
//最后一句不理解，感觉像是个条件，为什么放在这里。另外如果没有满足条件的新的节点怎么办？？
//另外刚开始的时候还没有B，那么岂不是A的范围，可以直接无穷大，那其他人都不用玩 了？？而且在算法执行过程中，并没有调整范围的说法，那不是先看谁，谁就比较牛逼吗？？

MLNN的应用

在使用MLNN的时候需要逐步确定一下内容：
1.符号化输入输出
2.选择训练数据
3.选择训练方法(Auswahl des Verfahren)
4.选择拓扑结构
5.参数调整(Parametereinstellung)

选择有代表性的训练数据

把训练数据分成三分
一份作为训练用(Lerndaten)，用以调整权值
一份作为测试用(Testdaten)，用于测试错误，过适应(overfitting)
一份作为确认用(Verifikationsdaten)，用于确定其普遍性
(für das Feststellen der Generalisierung)
那么什么才算是好得训练数据呢：
**分布均匀(gute Verteilung)
对于分类问题来说，数据应该来自所有的类。
而对于回归问题来说，数据应该来自整个定义域。
包含有复杂区域的数据(komplexe Regionen):
如边缘区域的数据或两个类的交界
//Verlaufsänderungen???不知在这里表示什么意思????

知识表达

如上图表示MLNN中的改变是全局性的(global)而RBF是局部的
/*几个比较的准则，没看懂？？？？
Verteilt(global)-Sigmoid MLNN
Änderungen wirken sich global aus
Generalisierung ist gut
Lokal RBF-NN
Änderungen nur lokal
Generalisierung schlechter
Vergleichskriterien:
Zielsetzung:Generalisierungsverhalten(verteilt)
Inkrementelles Lernen(Beibehalten von Wissen:eher lokal)
Interpretierbarkeit(lokal)
Einsatz in hybriden Lernarchitekturen(beide)
     Umsetzbarkeit von bzw. in Fuzzy-Wissenbasen(lokal)
*/

权值的初始化

不同的权值的初始化应该是不同的，否则这些权值初始相同的神经元会有相同的功能。
另外权值的初始化应该是随机的，均匀分布的，并且是小的。
( ⇒keineanfänglicheAusrichtung？？？？ 不知表达的是啥意思)

权值的调整

有两种调整方法：
Patternlerning:
在每次学习的例子后进行调整
这中方法的学习速度快
但不是真得梯度下降//???
随机顺序 → 更好的逼近//？？？
/*上面四句的原文
Anpassung nach jedem Lernbeispiel
schnelles Lernen
kein “echter” Gradientenabstieg
zufällige Reihenfolge → gute Approximation
*/
Epochlearning:
权值改变为所有学习例子对应的权值改变的均值
在所有例子都学完后进行权值调整
这才是真得梯度下降
对错误的和离谱的训练数据不敏感
/*同上
Mittelung der Gewichtsänderung über alle Beispiele
Anpassung nachdem alle Beispiele propagiert wurden
“echter” Gradientenabstieg
nicht anfällig für Ausreißer/falsche Lerndaten
*/

过适应(Overfitting)

//后面还有几个实际应用的例子，实在没有精力了。