二次 贝塞尔曲线 和三次 贝塞尔曲线 使用说明
- 1. 二次 贝塞尔曲线 和三次 贝塞尔曲线
- 1.1 贝塞尔曲线的 基本知识
- 1.2 贝塞尔曲线 生成动图
- 1.3 HTML 中 画贝塞尔曲线的 2 种方法
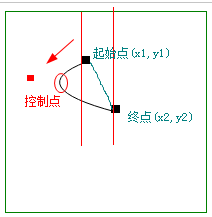
- 1.4 二次 贝塞尔曲线
- 1.4.1 二次 贝塞尔曲线的创建
- 1.4.2 二次 贝塞尔曲线的 弯曲处宽窄控制
- 1.4.3 二次 贝塞尔曲线的 伸缩和平移
- 1.4.4 二次 贝塞尔曲线 控制点的取值 和弯曲方向
- 1.4.5 二次 贝塞尔曲线 使用示例
- 1.5 三次 贝塞尔曲线
- 1.5.1 三次 贝塞尔曲线的 生成动图和创建
- 1.5.2 三次 贝塞尔曲线的 起始点
- 1.5.3 三次 贝塞尔曲线的 弯曲处的 宽窄控制
- 1.5.4 三次 贝塞尔曲线 弯曲处的 拉伸
- 1.5.5 三次 贝塞尔曲线的 控制点的 坐标取值
1. 二次 贝塞尔曲线 和三次 贝塞尔曲线
1.1 贝塞尔曲线的 基本知识
- 贝塞尔曲线的 基本知识
-
① 贝塞尔曲线本质: Bézier curve (贝塞尔曲线)= 曲线 = 用于二维图
-
② 曲线定义:起始点、终止点(也称锚点)、控制点。
-
③ 调整曲线形状: 调整控制点起始点.终点的坐标值 = 调整曲线形状
-
④ 贝塞尔曲线名称由来: 1962年,法国数学家 Pierre Bézier 第一个研究了这种 矢量绘制曲线 的方法,并给出了详细的计算公式,因此按照公式 绘的曲线 就用他的姓氏 来命名.
-
参考博文
- 贝塞尔曲线讲解 1
- 贝塞尔曲线讲解 2 - 数学原理
1.2 贝塞尔曲线 生成动图
- 贝塞尔曲线 生成动图
- ① 一阶(一次)贝塞尔曲线( = 线段):

- ② 二次贝塞尔曲线( = 抛物线)
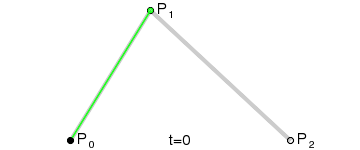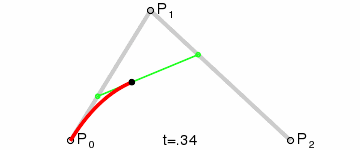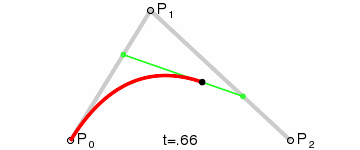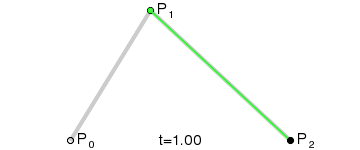
- ③ 三次贝塞尔曲线( = 类似抛物线的圆滑曲线)
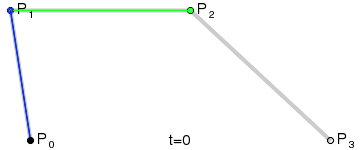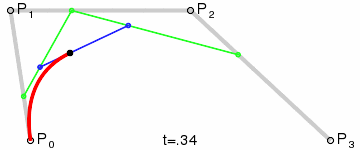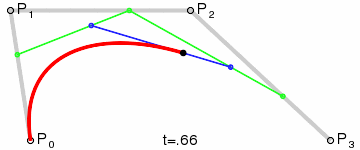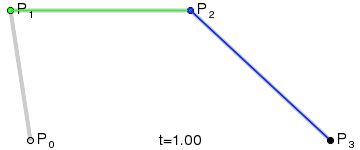
1.3 HTML 中 画贝塞尔曲线的 2 种方法
- 画贝塞尔曲线的 2 种方法
- ① 二次贝塞尔曲线: = 1个控制点 + 1个结束点
- 使用
quadraticCurveTo(cp1x, cp1y, x, y)二次 贝塞尔曲线到点 方法
- quadratic [kwɑ’drætɪk] adj. [数] 二次的
- 参数: (cp1x,cp1y) = 1个控制点,(x,y) = 1个结束点。
- ② 三次贝塞尔曲线: = 2个控制点 + 1个结束点
- 使用
bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y)三次 贝塞尔曲线到点 方法
- 参数: (cp1x,cp1y) = 控制点一,(cp2x,cp2y) = 为控制点二,(x,y)= 1个结束点。
1.4 二次 贝塞尔曲线
1.4.1 二次 贝塞尔曲线的创建
<body>
<canvas id="myCanvas" height="200px" width="200px" style="border:1px solid green">
一条 二次 贝塞尔曲线
canvas>
<script type="text/javascript">
var canvas=document.getElementById("myCanvas");
if(canvas.getContext){
var ctx=canvas.getContext("2d");
ctx.beginPath();
ctx.moveTo(75,25);
ctx.quadraticCurveTo(25,25,25,60);
ctx.stroke();
}
script>
body>
| 1 条贝塞尔曲线 |
起点和终点 |
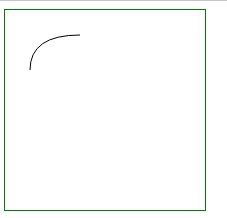 |
 |
- 测试
- 显示曲线: 二次贝塞尔曲线,显示一段 起始点到终点的曲线
- 曲线弯曲方向: 控制点不会显示出来,曲线弯曲方向,朝向 控制点的坐标位置
- 改变曲线方向 = 改变 控制点的坐标 (不改变 起始点和终点时)
- 改变曲线的形状: 改变 起始点,终点,控制点坐标,都可以 改变曲线的形状
- 示例2: 上方曲线,把控制点坐标 变成
(10,10)和(100,100),看曲线 弯曲方向的变化

1.4.2 二次 贝塞尔曲线的 弯曲处宽窄控制
- 示例1:
- (二次 贝塞尔曲线) 弯曲处的宽窄控制:控制点坐标 不变,改变 起始点和终点的坐标
- ① 弯曲处变宽: = 增加 坐标差 a,b (起始点和终点的坐标差)
- (假设 起始点和终点之间的坐标差,a=x1-x2,b=y1-y2,两个点,x1,x2之间距离变远,y1和y2之间 距离变远)
- 改坐标值: 大大小小 (把较大值加大,较小值减小,增加距离)
- ②弯曲处变窄: 缩小 坐标差 a,b (起始点和终点的坐标差)
- (假设 起始点和终点之间的坐标差,a=x1-x2,b=y1-y2) ,x1和x2之间距离 越来越靠近,y1和y2 之间的距离变近
- 改坐标值:大小小大 (把较大值减小,较小值加大,减少距离)
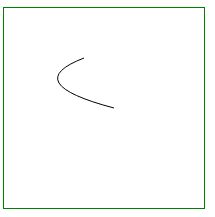
<body>
<canvas id="myCanvas" height="200px" width="200px" style="border:1px solid green">
一条 二次 贝塞尔曲线
canvas>
<script type="text/javascript">
var canvas=document.getElementById("myCanvas");
if(canvas.getContext){
var ctx=canvas.getContext("2d");
ctx.beginPath();
ctx.moveTo(80,50);
ctx.quadraticCurveTo(15,75,110,100);
ctx.stroke();
}
script>
body>
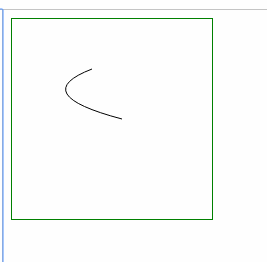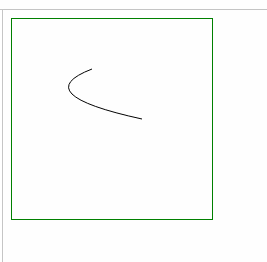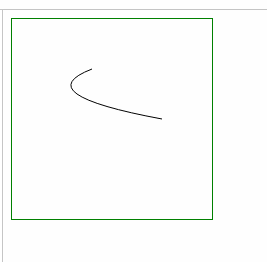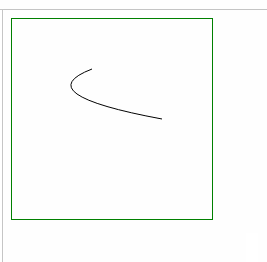
- ⑴ 弯曲处变宽: = 增加 坐标差 a,b (起始点和终点的 x坐标差,y坐标差)
| 左右变宽: 增大 较大的x横坐标 |
左右变宽: 减小 较小的x横坐标 |
 |
 |
| 上下变宽: 增大 较大的y横坐标 |
上下变宽: 减小 较小的y横坐标 |
 |
 |
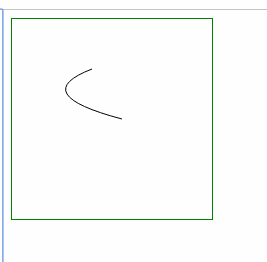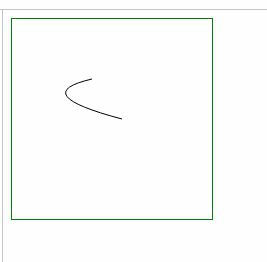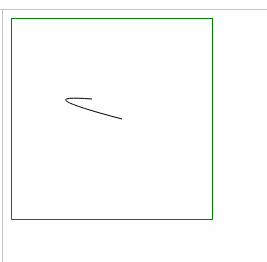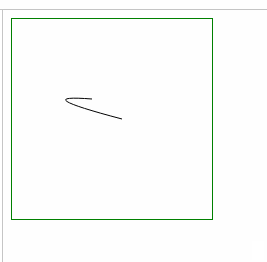
- ⑵ 弯曲处变窄: 缩小 坐标差 a,b (起始点和终点的 x坐标差,y坐标差)
| 左右变窄: 增大 较小的x横坐标 |
左右变窄: 减小 较大的x横坐标 |
 |
 |
| 上下变窄: 增大 较小的y横坐标 |
上下变窄: 减小 较大的y横坐标 |
 |
 |
1.4.3 二次 贝塞尔曲线的 伸缩和平移
- ⑴ 二次 贝塞尔曲线的伸缩: 两点和控制点的坐标差
- 伸长曲线: 增加 两点和控制点的坐标差 (起始点和终点,和控制点的坐标差)
- a1=x1-cp1x,a2=x2-cp1x,b1=y1-cp1y,b2=y2-cp1y)
- (a1,b1)=起始点-控制点
- (a2,b2)=终点-控制点
- 缩短曲线:减少 两点和控制点的坐标差
- 伸缩方向: 伸缩 左右方向,改x,伸缩 上下方向,改y
- ① 伸长曲线: 伸长左右方向 和伸长上下方向 = 增加 两点和控制点的坐标差
| 左右伸长:改起始点 x坐标值 |
左右伸长:改终点 x坐标值 |
 |
 |
| 上下伸长:改起始点 y坐标值 |
上下伸长:改终点 y坐标值 |
 |
 |
- ② 缩短曲线: 缩短左右方向 和缩短上下方向 = 减少 两点和控制点的坐标差
| 左右缩短:改 x坐标值 (起始点和终点) |
上下缩短: 改 y坐标值 (起始点和终点) |
 |
 |
- ⑵ 二次 贝塞尔曲线的平移
- 两点的x或y,同时增减相同值 a
- 左右平移: 改x值,起始点和终点,同时加减 a (y坐标值 保持不动)
- 上下平移: 改y值,起始点和终点,同时加减 a (x坐标值 保持不动)
- 总结: 平移的时候,一次 只改x坐标值或是y坐标值 (两个点 一起增减相同值)
| 左右平移 |
上下平移 |
 |
 |
1.4.4 二次 贝塞尔曲线 控制点的取值 和弯曲方向
- 二次 贝塞尔曲线 控制点的取值 和弯曲方向
- ① 向左右弯曲: 改控制点 x值 (相对于起始点和终点的连线) 起始点(x1,y1),终点(x2,y2),控制点(cp1x,cp1y)
- 向左弯曲: = 弯曲处 在左边
- cp1x < min (x1,x2) = 小于 最小x值
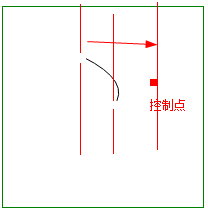
- 向右弯曲: = 弯曲处 在右边
- cp1x > max(x1.x2) = 大于 最大x值
- ② 向上下弯曲: 改控制点 y值
- 向上弯曲: cp1y < min (y1,y2) = 小于 最小y值
- 向下弯曲: cp1y > max(y1.y2) 大于最大y值
1.4.5 二次 贝塞尔曲线 使用示例
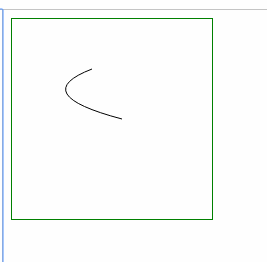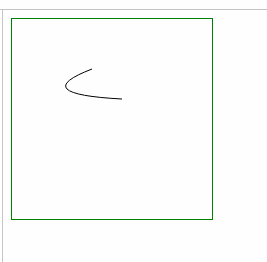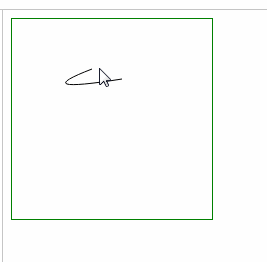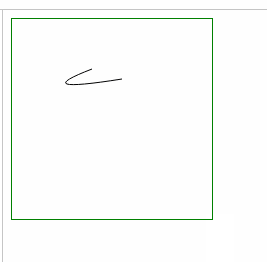
- 示例1: 多段 二次 贝塞尔曲线的使用: 添加连续的曲线,让每两条 二次贝塞尔曲线 相连,组成一个 绘画气泡窗口
<body>
<canvas id="myCanvas" height="200px" width="200px" style="border:1px solid green">
一个对话气泡图形
canvas>
<script type="text/javascript">
var canvas=document.getElementById("myCanvas");
if(canvas.getContext){
var ctx=canvas.getContext("2d");
ctx.beginPath();
ctx.moveTo(75,25);
ctx.quadraticCurveTo(25,25,25,60);
ctx.quadraticCurveTo(20,100,50,100);
ctx.quadraticCurveTo(50,125,25,120);
ctx.quadraticCurveTo(70,125,68,100);
ctx.quadraticCurveTo(165,115,152,50);
ctx.quadraticCurveTo(152,20,75,25);
ctx.stroke();
}
script>
body>
- 使用
quadraticCurveTo()二次贝塞尔曲线 到点函数,实现对话气泡的过程
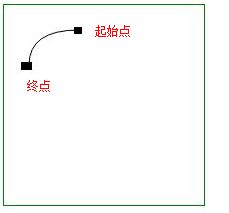
| 1条 贝塞尔曲线 ↓ |
起点和终点 |
 |
 |
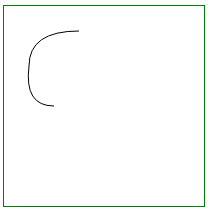
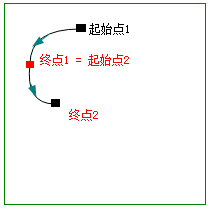
| 2条 贝塞尔曲线 (连接在一起) ↓ |
起点和终点 |
 |
 |
| 3条 贝塞尔曲线 ↓ |
起点和终点 |
 |
 |
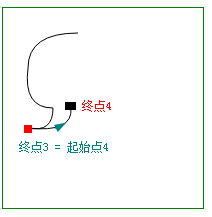
| 4条 贝塞尔曲线 ↓ |
起点和终点 |
 |
 |
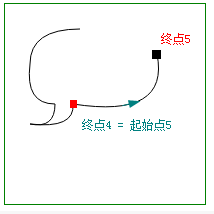
| 5条 贝塞尔曲线 ↓ |
起点和终点 |
 |
 |
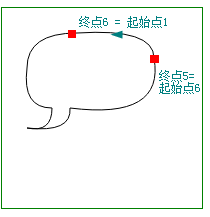
| 6 条贝塞尔曲线 (对话气泡)↓ |
起点和终点 |
 |
 |
- 测试
- 绘制过程显示: 在绘制过程中,先把
stoke()绘画 方法 写在后面,这样每画一条曲线,都能看见,利于 调整形状
- 坐标调整: 对于 起始点,终点,控制点的坐标调整
- 上下移动: 调整 y 值
- 左右移动: 调整 x 值
- 控制点相对于 终点和起始点的位置 进行限定
- 起始点
- 曲线第1个起始点: 使用
moveTo()移动到点 函数 创建
- 曲线接下来的起始点: 上一条曲线的终点 = 下一条曲线的起始点
- 弯曲处: 一条二次贝塞尔曲线,只有一个弯曲方向 = 只有一个弯曲处 (一般看有几个弯曲,就需要用几条曲线)
- 弯曲处是平滑的: 不平滑的连接处,一般是终点位置,不会是控制点的坐标
- 曲线弯曲方向: 朝向 控制点的坐标
- 曲线的数目: =
quadraticCurveTo()二次赛贝尔曲线到点 方法的使用数目
- 示例2: 对话气泡,6个弯曲处,所以用函数表示时,6个弯曲处 = 6条曲线 = 6个
quadraticCurveTo()函数

<body>
<canvas id="myCanvas" height="200px" width="200px" style="border:1px solid green">
心形
canvas>
<script type="text/javascript">
var canvas=document.getElementById("myCanvas");
if(canvas.getContext){
var ctx=canvas.getContext("2d");
ctx.beginPath();
ctx.moveTo(80,80);
ctx.quadraticCurveTo(22,40,35,100);
ctx.quadraticCurveTo(42,122,80,140);
ctx.quadraticCurveTo(120,122,122,100);
ctx.quadraticCurveTo(140,40,80,80);
ctx.stroke();
}
script>
body>
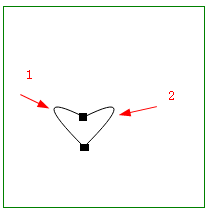
| 2条 二次贝塞尔曲线 (心形♡) ↓ |
起始点和终点 |
 |
 |
| 4条 二次贝塞尔曲线 (心形♡) ↓ |
起始点和终点 |
 |
 |
- 测试
- 弯曲度调整: 适当增加 曲线数目,有利于调整 图形的弯曲度
- 示例4: 把描边心形,变成填充心形
- 把
ctx.stroke()绘制方法 换成 ctx.fill()填充方法,会自动填充成 黑色

1.5 三次 贝塞尔曲线
1.5.1 三次 贝塞尔曲线的 生成动图和创建
- 三次贝塞尔曲线 形成动图
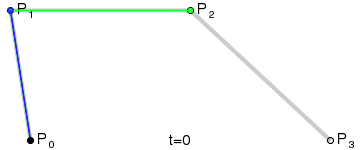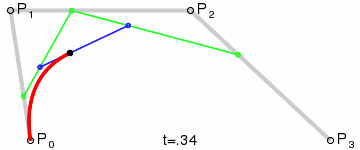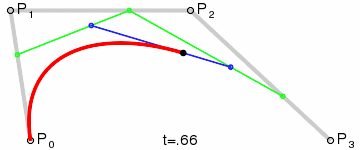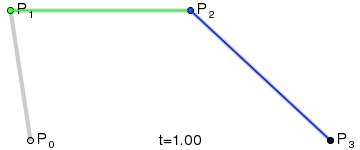
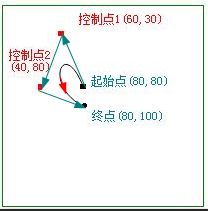
- 示例1: 一条 三次贝塞尔曲线
<body>
<canvas id="myCanvas" height="200px" width="200px" style="border:1px solid green">
一条 三次贝塞尔曲线
canvas>
<script type="text/javascript">
var canvas=document.getElementById("myCanvas");
if(canvas.getContext){
var ctx=canvas.getContext("2d");
ctx.beginPath();
ctx.moveTo(80,80);
ctx.bezierCurveTo(60,30,40,80,80,100);
ctx.stroke();
}
script>
body>
| 1条 三次贝塞尔曲线 |
起始点,终点和控制点 |
起始点,终点和控制点 连线 |
 |
 |
 |
- 示例2: 用 2条 三次贝塞尔曲线,画 1个描边心形
<body>
<canvas id="myCanvas" height="200px" width="200px" style="border:1px solid green">
心形
canvas>
<script type="text/javascript">
var canvas=document.getElementById("myCanvas");
if(canvas.getContext){
var ctx=canvas.getContext("2d");
ctx.beginPath();
ctx.moveTo(80,75);
ctx.bezierCurveTo(60,35,25,80,80,100);
ctx.bezierCurveTo(140,65,85,40,80,75);
ctx.stroke();
}
script>
body>
| 2条 三次贝塞尔曲线 (心形) |
起始点和终点 |
 |
 |
1.5.2 三次 贝塞尔曲线的 起始点
- 三次 贝塞尔曲线的 起始点
- 第一条曲线的起始点: 用
moveTo()移动到点 方法设置的起始点
- 接下来的起始点: = 前一条曲线的终点 = 下一条曲线的起始点
1.5.3 三次 贝塞尔曲线的 弯曲处的 宽窄控制
- ⑴ 弯曲处的宽窄: 改 2 控制点的坐标差,增大或缩小
- = 控制点之间的 x 坐标差和 y 坐标差(横坐标和纵坐标)
- ① 曲线 弯曲处变窄: = 缩小 控制点坐标差
- 两个 x 横坐标值 越接近( cp1x-cp2x ) = 两个 y 纵坐标值 越接近( cp1y-cp2y ) = 曲线 弯曲处的两条边 之间的距离越小
- 缩小 控制点坐标差的 方法: 较小坐标变大,较大坐标变小,缩短距离 = 2个坐标值 距离越来越接近
- ② 曲线 弯曲处变宽: = 增大 控制点坐标差 = 2 个坐标值 距离越来越远
| 左右变窄: 大小= 增大 较小的 x坐标值 |
左右变窄: 小大= 减小 较大的 x的坐标值 |
 |
 |
| 上下变窄: 大小= 增大 较小的 y坐标值 |
上下变窄: 小大= 减小 较大的 y坐标值 |
 |
 |
| 左右变宽: 大大= 增大 较大的 x坐标值 |
左右变宽: 小小= 减小 较小的 x的坐标值 |
 |
 |
| 上下变宽: 大大= 增大 较大的 y坐标值 |
上下变窄: 小小= 减小 较小的 y坐标值 |
 |
 |
1.5.4 三次 贝塞尔曲线 弯曲处的 拉伸
- ⑴ 曲线 弯曲处拉伸: = 2 控制点,同时改x值,或y值,改的值相同
- = (改的值相同,坐标差不变)
- ① 曲线 弯曲处 向左右拉伸: = 2 个控制点 同时改 x值,改的值相同,y 值不动
- 2 个控制点的纵坐标不变
- 横坐标差 也不变
- 把 cp1x 和 cp2x 横坐标减少 a (同时减少相同值 a)
- ② 曲线 弯曲处 向上下拉伸: 2个控制点 同时改y值,改的值相同,x值不动
- 保持坐标差不变(不从控制点上改变宽窄),拉伸宽窄改变= 由和起始点终点之间的相对距离改变
- 总结:
- 弯曲处宽窄 = 增减 2 个控制点的 坐标差
- 弯曲处拉伸 = 同时改2个控制点的x值,或y值, 改的值相同.(一次 只改 2 个 x值,或只改 2 个y值)
- 宽窄和拉伸 方向: 左右:改 x,上下: 改 y值
| 向左拉伸: cp1x,cp2x 同时减 a(坐标差不变) |
向右拉伸: cp1x,cp2x 同时加 a(坐标差不变) |
 |
 |
| 向上拉伸: cp1y,cp2y 同时减 a(坐标差不变) |
向下拉伸: cp1y,cp2y 同时加 a(坐标差不变) |
 |
 |
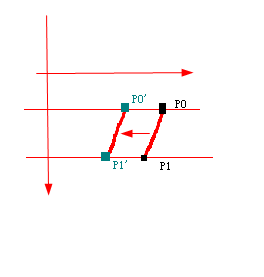
- ⑶ 曲线 左右拉伸 和控制线段 的关系:
- 控制线段的左右平移 = 保持纵坐标不变,横坐标差也不变,横坐标同时增减 a(针对2个控制点) = 控制点P0,P1之间的线段,向左右平移 a 距离
| 控制线段P0P1 向左平移 = 同时减少横坐标(纵坐标不变减少相同量a) |
|
 |
|
1.5.5 三次 贝塞尔曲线的 控制点的 坐标取值
- 控制点的坐标取值
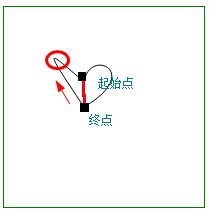
- 弯曲处方向,在左上方: (相对于 起始点和终点之间的 连接线段)
- cp1x和cp2x < min (起始点x,终点x)
- cp1y和cp2y < min (起始点y,终点y)
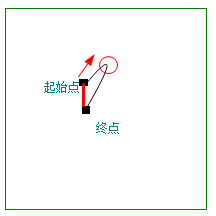
- 弯曲处方向,在右上方
- cp1x和cp2x > max (起始点x,终点x)
- cp1y和cp2y < min (起始点y,终点y)
- 弯曲处方向,在右下方
- cp1x和cp2x > max (起始点x,终点x)
- cp1y和cp2y > max (起始点y,终点y)
- 弯曲处方向,在左下方
- cp1x和cp2x < min (起始点x,终点x)
- cp1y和cp2y > max (起始点y,终点y)
| 弯曲处于 左上方 |
弯曲处于 右上方 |
 |
 |
| 弯曲处于 右下方 |
弯曲处于 左下方 |
 |
 |
- 总结:控制点取值 和弯曲处位置关系(相对于 开始点和终点之间的线段,要先确定 起始点和终点坐标)
- ① 弯曲处的左右控制:
- 向左弯曲: = 弯曲处 在左边= 小于 x最小值
- 控制点的横坐标 ,要小于 起始点和终点的横坐标,距离越远,拉伸越长
- cp1x和cp2x < min (起始点x,终点x) ,小于 x最小值
- 向右弯曲: = 弯曲处 在右边 = 大于 x最大值
- 控制点的横坐标,要大于起始点和终点的横坐标,距离越远,拉伸越长
- cp1x和cp2x > max (起始点x,终点x) ,大于 x最大值
- ② 弯曲处的上下控制:
- 向上弯曲: = 弯曲处 在上方 = 小于 y最小值
- cp1y和cp2y < min (起始点y,终点y) ,小于 y最小值
- 向下弯曲: = 弯曲处 在下方 = 大于 y最大值
- cp1y和cp2y > max (起始点y,终点y) = 大于 y最大值
- 捐助: 喜欢这篇文章吗? 捐助此文,向团团 表示鼓励和支持吧~❤

- 捐助二维码: