剑指offer面试题：14剪绳子

题目

给你一根长度为n的绳子，请把绳子剪成m段 (m和n都是整数，n>1并且m>1)每段绳子的长度记为k[0],k[1],…,k[m].请问k[0]k[1]…*k[m]可能的最大乘积是多少？例如，当绳子的长度为8时，我们把它剪成长度分别为2,3,3的三段，此时得到的最大乘积是18。

分析

1. 归纳法分析---其他博客的做法
2. 题型类似于斐波那契数列思想，当前问题求解依赖于上一个子问题的解决，求长度n的最大乘积依赖于求解长度n-1。将大问题长度n依次化解成小问题求长度n-1，再求长度n-2.....最后问题变成求解长度 2。从小长度n=2，逐层回溯，就得到大长度n的结果。也就是递归法----本文特色，看代码
3. 形如  f(n)=max {f(n-i)*f(i)} 或者f(n)=min {f(n-i)*f(i)} 求最优解，解的数目不唯一-----符合动态规划要求，直接用动态规划方法，归纳法和递归法得到的结果也是动态规划思想的变形。常见经典动态规划：礼物最大值问题，背包问题，硬币找零

• 归纳法

绳子的最小基础剪发可以分为2 或3， 也就是，当数据中全是由2 或3 组成时，相乘的结果最大。因此，由小至大，

　　* 绳子的长为2时，只能剪成1 1，即f(2) = 1x1 = 1;

　　* 当绳子长为3时，可能将绳子剪成长度为1 2 或者1 1 1，由于1 x 2 > 1 x 1 x 1,因此f(3)=2;
　　* 当绳子长为4时，可能将绳子剪成长度为2 2 或者 1 2 1 或者1 1 1 1或者 1 3，由于2 x 2 > 其他，因此f(4)=2*2
　　* 当绳子长为5时，可能将绳子剪成长度为3 2 或者...，由于3 x 2 > 其他，因此f(5)=3*2;
　　* 当绳子长为6时，可能将绳子剪成长度为3 3 或者...，由于3 x 3 > 其他，因此f(6)=3*3=9;//不使用f(3)因为3为最小单位中的最大值
　　* 当绳子长为7时，可能将绳子剪成长度为4 3 或者...，由于4 x 3 > 其他，因此f(7)=f(4)*3=2*2*3=12；我们的算法求解范围为由1-n。由小向大算，因此f(4)我们已经算出来了，直接使用即可，不必重复计算。
　　* 当绳子长为8时，可能将绳子剪成长度为2 6 或者...，因此f(8)=f(6)*2=3*3*2=18;我们的算法求解范围为由1-n。由小向大算，因此f(6)我们已经算出来了，直接使用即可，不必重复计算。

　　同理，当绳子长为9时，比较2*f(7)的值和3*f(6)的值即可.当绳子长为10时，比较2*f(8)的值和3*f(7)的值即可..当绳子长为11时，比较2*f(9)的值和3*f(8)的值即可.

归纳出 除绳子长度小于4外，均满足 f(n)=max{f(n-i)*f(i)}

程序

•  归纳法

#include  
using namespace std;

int cutting(int n) 
{
  // 特殊绳长，长度为0、1、2、3,除此之外都是符合f(n)=max{f(n-i)*f(i)}
  if(n==1)    
    return 0;
  if(n==2)	
    return 1;
  if(n==3)  
    return 2;
    
  //绳子大于3情况,下面的初始化不代表着最大值，为了方便i>=4的计算,使得符合f(n)=max{f(n-i)*f(i)}
  int product[n]; 
  product[0]=0;
  product[1]=1;
  product[2]=2;
  product[3]=3;
  int Max;  
  if(n>3)
  {
  	for(int i=4;i

• 递归法

#include  
using namespace std;

//n cal分别传入绳子长度，函数cuttingRevise传出最优解
// cal 用来控制特殊值--绳长1 2 3时，n用来控制递归
int cuttingRevise(int n,int cal) 
{  //特殊绳长
  if(n==1&&cal<4)	
    return 0;
  if(n==2&&cal<4)  
    return 1;
  if(n==3&&cal<4)
    return 2;
  
  // 绳长大于3 
  if(n==0&&cal>3)    
    return 0;
  if(n==1&&cal>3)	
    return 1;
  if(n==2&&cal>3)  
    return 2;
  if(n==3&&cal>3)
    return 3;
  if(n>3)	
  {
  	int m=2,Max=0;  
  	while(m<=n/2)
  	{
  	  int k=cuttingRevise(m,cal)*cuttingRevise(n-m,cal); //递归，f(n)=f(n-i)*f(i) 	
  	  m++;  
	  if(Max

问题推广 

 礼物最大值

在一个 m*n 的棋盘中的每一个格都放一个礼物，每个礼物都有一定的价值（价值大于0）.你可以从棋盘的左上角开始拿各种里的礼物，并每次向左或者向下移动一格，直到到达棋盘的右下角。给定一个棋盘及上面个的礼物，请计算你最多能拿走多少价值的礼物？

  比如说现在有一个如下的棋盘，

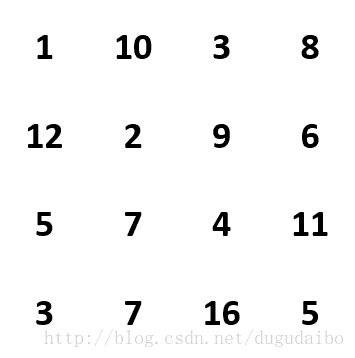
在这个棋盘中，按照（1，12，5，7，7，16，5）的顺序可以拿到总价值最大的礼物

背包问题

 假设山洞里共有a,b,c,d ,e这5件宝物（不是5种宝物），它们的重量分别是2,2,6,5,4，它们的价值分别是6,3,5,4,6，现在给你个承重为10的背包, 怎么装背包，可以才能带走最多的财富