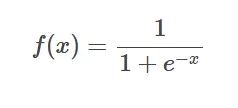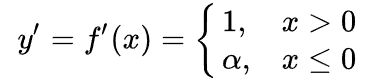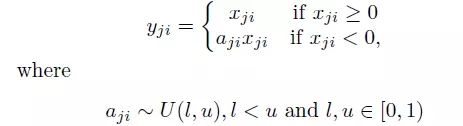机器学习之路二:激活函数,损失函数
激活函数
激活函数有什么用?
引入非线性因素。
在我们面对线性可分的数据集的时候,简单的用线性分类器即可解决分类问题。但是现实生活中的数据往往不是线性可分的,面对这样的数据,一般有两个方法:引入非线性函数、线性变换。
线性变换
就是把当前特征空间通过一定的线性映射转换到另一个空间,让数据能够更好的被分类。
激活函数(非线性函数)
激活函数是如何引入非线性因素的呢?在神经网络中,为了避免单纯的线性组合,我们在每一层的输出后面都添加一个激活函数(sigmoid、tanh、ReLu等等),这样的函数长这样:
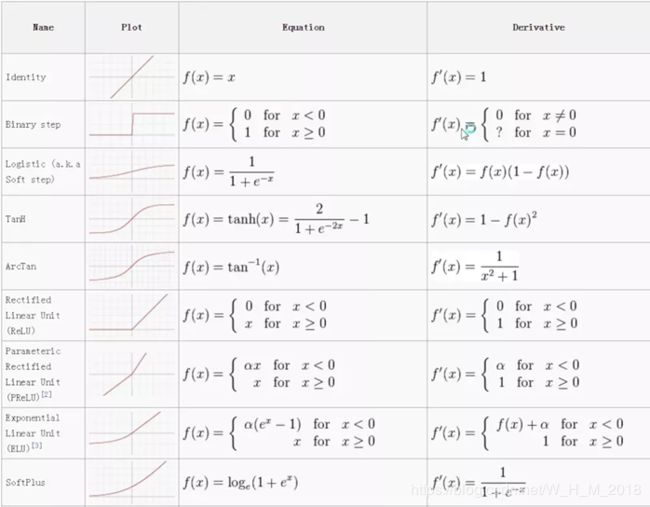
常见的传统激活函数主要有两个:sigmoid和tanh。
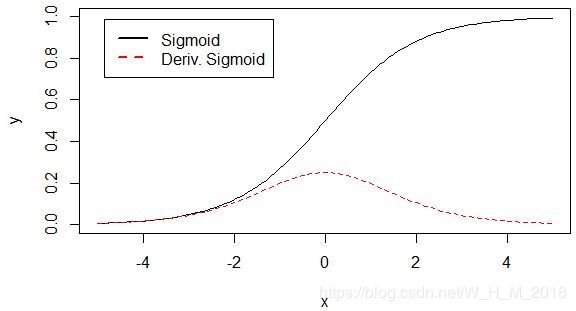
sigmoid函数
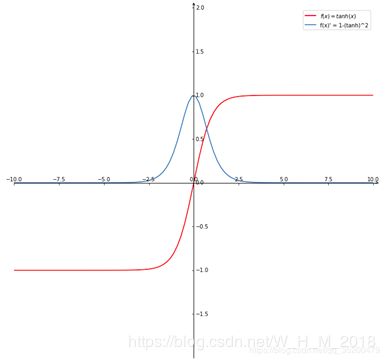
tanh函数
激活函数的饱和问题
当一个激活函数,既满足左饱和又满足又饱和时,我们称之为饱和。
硬饱和与软饱和
对任意的x,如果存在常数c,
当x>c时恒有 h′(x)=0则称其为右硬饱和,
当x 若既满足左硬饱和,又满足右硬饱和,则称这种激活函数为硬饱和。 但如果只有在极限状态下偏导数等于0的激活函数称为软饱和。 它是使用范围最广的一类激活函数,具有指数函数形状,在物理上最接近神经元。它的输出范围在(0,1)之间,可以被表示成概率,或者用于数据的归一化。 但是它有两个严重的缺陷: 1. 软饱和性——导数 f'(x)=f(x)(1-f(x)),当x趋于无穷时,f(x)的两侧导数逐渐趋于0。在后向传递时,sigmoid向下传递的梯度包含了一个f'(x)因子,因此,一旦落入饱和区f'(x)就变得接近于0,导致了向后传递的梯度也非常小。此时,网络参数很难得到有效训练,这种现象被称为梯度消失。一般在5层以内就会产生梯度消失的现象。 2. sigmoid函数的输出均大于0,这就使得输出不是0均值,这称为偏置现象。这将会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。 tanh函数与sigmoid函数相比,输出均值为0,这就使得其收敛速度要比sigmoid快,从而可以减少迭代次数。 缺点就是同样具有软饱和性,会造成梯度消失。 详解机器学习中的梯度消失、爆炸原因及其解决方法 https://blog.csdn.net/qq_25737169/article/details/78847691 针对sigmoid和tanh的饱和性,产生了激活函数ReLU、Leaky ReLU、PReLU和RReLU https://blog.csdn.net/qq_23304241/article/details/80300149 导数为 ReLU全称为Rectified Linear Units,可以翻译成线性整流单元或者修正线性单元。 它在x>0时不存在饱和问题,从而使保持梯度不衰减,从而解决了梯度消失问题。这让我们能够直接以监督的方式训练深度神经网络,而无需依赖无监督的逐层预训练。然而,随着训练的推进,部分输入会落入硬饱和区,导致对应权重无法更新,这种现象称为“神经元死亡” 与sigmoid类似,ReLU的输出均值也大于0,所以偏移现象和神经元死亡共同影响网络的收敛性。 ReLU是将所有的负值都设为零,相反,Leaky ReLU是给所有负值赋予一个非零斜率。Leaky ReLU激活函数是在声学模型(2013)中首次提出的。以数学的方式我们可以表示为: 导数为 a是(1,+∞)区间内的固定参数。 对于 Leaky ReLU 中的α,通常都是通过先验知识人工赋值的。然而可以观察到,损失函数对α的导数我们是可以求得的,可不可以将它作为一个参数进行训练呢?Kaiming He的论文《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》指出,不仅可以训练,而且效果更好。公式非常简单,反向传播至未激活前的神经元的公式就不写了,很容易就能得到。对α的导数如下:δyiδα=0,(ifyi>0),else=yi原文说使用了Parametric ReLU后,最终效果比不用提高了1.03%. 是 leaky ReLU 的random 版本 (α是random的).它首次试在 kaggle 的NDSB 比赛中被提出的。核心思想就是,在训练过程中,α是从一个高斯分布U(l,u)中 随机出来的,然后再测试过程中进行修正(有点像dropout的用法)。数学表示如下: PReLU中的ai是根据数据变化的; Leaky ReLU中的ai是固定的; RReLU中的aji是一个在一个给定的范围内随机抽取的值,这个值在测试环节就会固定下来。 它结合了sigmoid和ReLU函数,左侧软饱和,右侧无饱和。 右侧线性部分使得ELU能缓解梯度消失,而左侧软饱和能让对ELU对输入变化或噪声更鲁棒。ELU的输出均值接近于0,所以收敛速度更快。 https://blog.csdn.net/qq_20909377/article/details/79133981 Maxout模型实际上也是一种新型的激活函数,在前馈式神经网络中,Maxout的输出即取该层的最大值,在卷积神经网络中,一个Maxout feature map可以是由多个feature map取最值得到。 maxout的拟合能力是非常强的,它可以拟合任意的的凸函数。但是它同dropout一样需要人为设定一个k值。 为了便于理解,假设有一个在第i层有2个节点第(i+1)层有1个节点构成的神经网络。 激活值 out = f(W.X+b); f是激活函数。’.’在这里代表內积 那么当我们对(i+1)层使用maxout(设定k=5)然后再输出的时候,情况就发生了改变。 此时网络形式上就变成上面的样子,用公式表现出来就是: z1 = W1.X+b1; z2 = W2.X+b2; z3 = W3.X+b3; z4 = W4.X+b4; z5 = W4.X+b5; out = max(z1,z2,z3,z4,z5); 也就是说第(i+1)层的激活值计算了5次,可我们明明只需要1个激活值,那么我们该怎么办?其实上面的叙述中已经给出了答案,取这5者的最大值来作为最终的结果。 总结一下,maxout明显增加了网络的计算量,使得应用maxout的层的参数个数成k倍增加,原本只需要1组就可以,采用maxout之后就需要k倍了。 再叙述一个稍微复杂点的应用maxout的网络,网络图如下: 对上图做个说明,第i层有3个节点,红点表示,而第(i+1)层有4个结点,用彩色点表示,此时在第(i+1)层采用maxout(k=3)。我们看到第(i+1)层的每个节点的激活值都有3个值,3次计算的最大值才是对应点的最终激活值。我举这个例子主要是为了说明,决定结点的激活值的时候并不是以层为单位,仍然以节点为单位。 以下解释更详细 https://www.cnblogs.com/lliuye/p/9486500.html https://www.jianshu.com/p/dc4e53fc73a0 https://blog.csdn.net/c123_sensing/article/details/81531519 激活函数的各种解释 https://www.cnblogs.com/missidiot/p/9378079.html https://www.jianshu.com/p/679510adf9a4 https://blog.csdn.net/qq_34886403/article/details/83280726 https://blog.csdn.net/willduan1/article/details/73694826 sigmoid函数
tanh函数
梯度消失和梯度爆炸
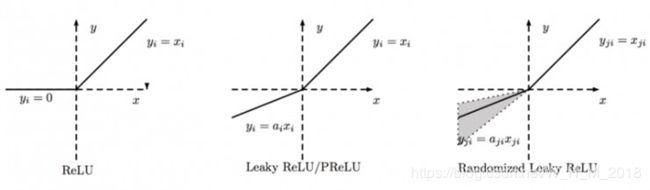
ReLU函数
Leaky-Relu函数
Parametric ReLU:
Randomized Leaky ReLU
ELU函数
ReLU、LReLU、PReLU、CReLU、ELU、SELU
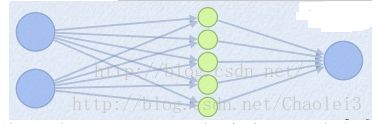
Maxout
![]() ;
; ![]()
损失函数
神经网络的损失函数
神经网络Loss损失函数总结