Andrew Ng机器学习笔记（一）

第一篇博客，很有纪念意义，献给让人激动人心的ML，也感谢吴恩达老师的精彩讲解。

我觉得，真正理解一个东西，要能够用通俗易懂的方式将它讲述出来。吴恩达老师的课是这方面的典型代表。

1.机器学习的定义

假设用P来评估计算机程序在某任务类T上的性能，若一个程序通过利用经验E在T中任务上获得了性能改善，则我们就说关于T和P，，改程序对E进行了学习。 —— [ Mitchell,1997 ]

2.机器学习算法分类

• supervised learning ：我们教计算机如何做事情
• unsupervised learning：计算机自己学习
• reinforcement learning
• recommender systems

监督学习：对于训练的数据集，标示明确的实际结果（如标明样本的房价，肿瘤的良性与恶性）。可分为：

监督学习{回归(Regression)分类(Classification)预测的是连续值预测离散值

非监督学习：在非监督式学习中，数据并不被特别标识，学习模型是为了推断出数据的一些内在结构。非监督学习中，数据将会被分为不同的 cluster(簇),称为cluster algorithm。如新闻网页的专题分类。

3.单变量线性回归

算法的工作原理如下图。用训练集“喂养”我们的学习算法，形成假设函数 h 。然后，对输入的x值，输出相应的预测值y。相当于是存在一个映射关系： y=f(x)

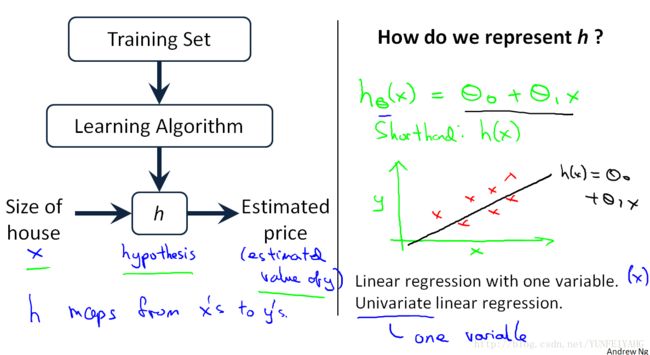
代价函数：用来选择最合适的曲线。在假设函数 hθ 中,有两个未知量，选择不同的参数值，最终的效果肯定是不一样的，如下图。

那么该如何选择呢？我们的想法是，选择某个 θ0 和 θ1 ，使得对于样本 (x,y) ， hθ(x) 最“接近”于 y 。越是“接近”，表明我们的假设函数越是精确。对于“接近”的刻画，让我们给出数学上的标准定义：

minimizeθ0,θ112m∑i=1m(hθ(x(i))−y(i))2

在线性回归中，我们要解决的是一个最小化问题。其中的 12 只是为了后面计算的方便。
我们记

J(θ0,θ1)=12m∑i=0m(hθ(x(i))−y(i))2

这样我们就得到了代价函数(cost function)。此处也称为平方误差函数，当然也有其他的代价函数。但是对于大多数问题，尤其是回归问题，平方误差函数都是一个合理的选择，“其可能是解决回归问题最常用的手段了”。
如此，我们的目标就是要让代价函数最小：

minimizeθ0,θ1J(θ0,θ1)

代价函数如何工作：
为了更方便地探究 hθ(x) 与 J(θ0,θ1) 的关系, 先令 θ0 等于0, 得到了简化后的假设函数 hθ(x)=θ1x ，如下图所示。

参数 θ1 是我们要确定的，对于不同的 θ1 ，我们可以画出不同的假设函数曲线，进而算出相应的代价函数值（代价函数取名是很到位的，由于 我们不知道真实具体的函数关系，那么我们所有的假设都会存在一定的偏差，也就是要付出的代价，我们所有做的事情就是要让这个代价变得最小）。代价函数，反应了每一种假设情况下我们要付出的“代价”。反应在图中，如下：

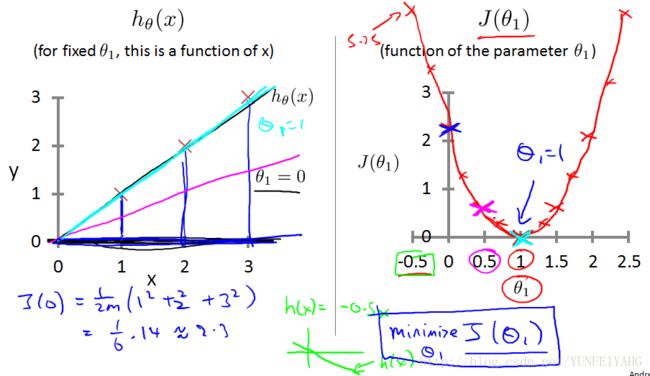
通过观察 J(θ1) 的函数图像，我们可以找到最小值时对应 θ1 值。在本例中， θ1=1 。

代价函数的进一步理解：
现在研究代价函数 J 是如何在最初的线性回归公式中工作。
此时，不再假设 θ0=0 ，存在两个变量 θ0 、 θ1 ，那么代价函数为 J(θ0,θ1) 。而且，我们知道这是一个三维的曲面。回顾上一节单变量情况下代价函数的特点，可知这个三维曲面是“碗型的”，如下：

为了方便讨论，一般将其表示为“等高线图”，以二维的形式予以展现。对于不同的 θ0 和 θ1 ，我们仍然可以计算得出相应的代价函数。越靠近中心，代价函数越小，离我们最终的理想结果越接近。我们可以不断地进行调试，得到不同的数值。那么，有没有比较快速的方法来达到目的呢？这就需要介绍下面的梯度算法了。

梯度下降算法：
梯度下降算法是一种优化算法, 它可以帮助我们找到一个函数的局部极小值点。
首先要知道方向导数、偏导数与梯度的概念。它们均涉及到函数的变化率，也就是增长的问题。对于高维函数，偏导数只是函数在坐标轴方向的变化率，但是很明显，函数可以有无数个方向（在xy平面内考虑）的变化，也就是方向导数。梯度，则是这所有中函数值增长最快的方向，考虑山丘地形，意味着最陡峭的地方。那么，我们的代价函数目标则是求最小值，只要沿着梯度相反方向，就可以最快到达目的地了。
算法描述：

迭代设计如下。在理解梯度概念的基础上，可以很方便推导出来。 其中 := 表示赋值， α 叫做学习速率，用来控制下降的幅度， ∂∂θjJ(θ0,θ1) 求偏导。这里一定要注意的是，算法每次是同时(simultaneously)改变 θ0 和 θ1 的值

下图介绍梯度下降法是如何工作的。十分像水的流动。

梯度下降算法中学习率和偏导数的理解：

首先看偏导数的影响，为了研究问题的方便，仍然令 θ0 等于0。那么偏导数降维到导数。

无论初始点选择在哪里，偏导数都能指出正确的下降方向。如下图所示：

而对于学习速率来说，取太小则迭代过程会很慢，取过大可能会发散最后。

可以这样说，偏导数决定迭代的方向，学习率则控制着迭代迈开的步子。在学习率取值适当的情况下，梯度下降有“自刹车”的功效。也就是说，越接近最低点时候，由于梯度越来越小，即使学习率保持不变，仍然能保证步子越来越小。这样，我们在迭代过程中，保持学习率为常数值即可。

最终的迭代公式：

将之前的代价函数和我们的梯度下降算法结合起来

那么可以得到如下完整的迭代算法：

给定初始值，按照此步骤即可找到对应最小代价函数时候的 θ0 和 θ1 的值，也即我们最终需要的假设函数。