项目反应理论 EM估计

项目反应理论参数的EM估计

写在前面：

本文主要描述了整个IRT使用EM算法参数的估计过程，其中涉及大量公式，如只是需要了解IRT相关基础知识，请转战wiki～～
预警： 大量公式来袭～～

---

IRT（项目反应理论）广泛应应用于心理测量学，相比CTT（传统测量理论）的主要优势在于不依赖于样本，能够为被试者提供具有一致性的测量结果。

IRT的基本假设：

1. 单维性，即能力是单维度的。
2. 局部独立性， 即项目间局部独立。
3. 项目反应函数假设，即被试者对项目对反应符合项目反应方程。

IRT 模型：

常见的IRT模型包括2PL模型和3PL模型，其中2PL模型表达式如下：

$p_{i,j}\left({\theta }_i\right)=\frac{1}{1+\exp \left[-D{a}_j\left({\theta }_i-b_j\right)\right]}$
其中 ${\theta }_i$表示被试者的能力， $a_j$是项目的区分度， $b_j$是项目的难度，D=1.7。

参数估计：

对于IRT参数估计有多种方法，如对于项目参数的估计有：边际极大似然估计（MMLE），极大边际后验法（MMAP），EM，MCMC等方法，对于能力参数的估计有极大似然（MLE），贝叶斯众数法（MAP），贝叶斯后验期望估计法（EAP）等。本文重点介绍对项目参数的EM估计。

建模：

1. 被观测数据$\mathbf{Y}$是N*J维的，N表示有N个被试者，J表示有J个题目，$\mathbf{Y}=\left({\mathbf{y}}_1,{\mathbf{y}}_2,\dots ,{\mathbf{y}}_N\right)$，${\mathbf{y}}_i=\left(y_{i1},y_{i2},\dots ,y_{iJ}\right)$，其中$y_{ij}$表示第i个被试者回答第j道题目的答案；
2. 不可观测变量为$\mathbf{\theta }=\left({\theta }_1,{\theta }_2,\dots ,{\theta }_N\right)$ 其中${\theta }_i$是第i个被试者的能力值，模型中假定${\theta }_i$只能取离散的值$q_k,k=1,\dots ,K$，对应取$q_k$的概率为${\pi }_k,k=1,\dots ,K$，即${\theta }_i$为多项式分布，其概率为：$\mathbf{\pi }=\left({\pi }_1,{\pi }_2,\dots ,{\pi }_K\right)$；不可观测变量为$\mathbf{\theta }=\left({\theta }_1,{\theta }_2,\dots ,{\theta }_N\right)$ 其中${\theta }_i$是第i个被试者的能力值，模型中假定${\theta }_i$只能取离散的值$q_k,k=1,\dots ,K$，对应取$q_k$的概率为${\pi }_k,k=1,\dots ,K$，即${\theta }_i$为多项式分布，其概率为：$\mathbf{\pi }=\left({\pi }_1,{\pi }_2,\dots ,{\pi }_K\right)$；
3. 完全数据为$\left[\left({\mathbf{y}}_1,{\theta }_1\right),\left({\mathbf{y}}_2,{\theta }_2\right),\dots ,\left({\mathbf{y}}_N,{\theta }_N\right)\right]$；完全数据为$\left[\left({\mathbf{y}}_1,{\theta }_1\right),\left({\mathbf{y}}_2,{\theta }_2\right),\dots ,\left({\mathbf{y}}_N,{\theta }_N\right)\right]$；
4. 待估计参数为项目参数$\mathbf{\Delta }=({\mathbf{\delta }}_1,{\mathbf{\delta }}_2,...{\mathbf{\delta }}_j)$，其中${\mathbf{\delta }}_j$为第j道题的参数。待估计参数为项目参数$\mathbf{\Delta }=({\mathbf{\delta }}_1,{\mathbf{\delta }}_2,...{\mathbf{\delta }}_j)$，其中${\mathbf{\delta }}_j$为第j道题的参数。

EM算法应用于IRT中是迭代估计$\mathbf{\Delta }$ 和$\mathbf{\pi }$:
E step: 根据给定的缺失数据的分布，观察数据和参数初始值，求完全数据的对数似然函数的条件期望。
M step: 极大化E-step给出的完全数据的对数似然函数的条件期望，求参数的值。

似然函数

给定观测变量$\mathbf{y}=\left(y_1,y_2,\dots ,y_J\right)$并假定能力参数分布为：$\pi =\left({\pi }_1,{\pi }_2,\dots ,{\pi }_J\right)$，项目参数为$\mathbf{\Delta }=({\mathbf{\delta }}_1,{\mathbf{\delta }}_2,...{\mathbf{\delta }}_j)$，则观测变量的条件概率分布为：

$f(\mathbf{y}|\mathbf{\Delta },\mathbf{\pi })={\sum }_{k=1}^{K}f\left(\mathbf{y},q_k|\Delta ,{\pi }_k\right)$ $={\sum }_{k=1}^{K}f(\mathbf{y}|q_k,\Delta ){\pi }_k$
由IRT的局部独立性假设，由于给定能力变量下项目反应结果是相互独立的，可得： $f(\mathbf{y}|q_k,\mathbf{\Delta })={\prod }_{j=1}^{J}P{\left(q_k|{\mathbf{\delta }}_j\right)}^{y_j}{\left[1-P\left(q_k|{\mathbf{\delta }}_j\right)\right]}^{1-y_j}$
其中 $P\left(q_k|{\mathbf{\delta }}_j\right)$是题目j的项目特征曲线，描述了给定能力下项目j答对的概率。由上式可以推出，完全数据的似然函数为： $\begin{array}{rl}L(\mathbf{Y},\mathbf{\theta }|\mathbf{\Delta },\mathbf{\pi })& =\prod _{i=1}^N\prod _{j=1}^{J}P{\left({\theta }_i|{\mathbf{\delta }}_j\right)}^{y_{ij}}{\left[1-P\left({\theta }_i|{\mathbf{\delta }}_j\right)\right]}^{1-y_{ij}}f\left({\theta }_i|\mathbf{\pi }\right)\\ & =\prod _{j=1}^J\prod _{i=1}^{N}P{\left({\theta }_i|{\mathbf{\delta }}_j\right)}^{y_{ij}}{\left[1-P\left({\theta }_i|{\mathbf{\delta }}_j\right)\right]}^{1-y_{ij}}f\left({\theta }_i|\mathbf{\pi }\right)\\ & =\prod _{j=1}^J\prod _{k=1}^{K}P{\left({\theta }_k|{\mathbf{\delta }}_j\right)}^{r_{jk}}{\left[1-P\left(q_k|{\mathbf{\delta }}_j\right)\right]}^{n_k-r_{jk}}{\pi }_k^{n_k}\end{array}$
其中， $f\left({\theta }_i|\mathbf{\pi }\right)={\pi }_k$ if ${\theta }_i=q_k$， $n_k$是N个被试者中能力为 $q_k$的人数， ${\mathbf{r}}_{jk}$则是 $n_k$人中答题正确的人数。
为方便计算，将上式化成对数似然函数为： $\log [L(\mathbf{R},\mathbf{n}|\mathbf{\Delta },\mathbf{\pi })]={\sum }_{j=1}^J{\sum }_{k=1}^K{r}_{jk}\log \left[P\left(q_k|{\mathbf{\delta }}_j\right)\right]+\left(n_k-r_{jk}\right)\log \left[1-P\left(q_k|{\mathbf{\delta }}_j\right)\right]+n_k\log \left[{\pi }_k\right]$

E-Step:

E步估计隐变量$\mathbf{\theta }$，在给定项目参数${\mathbf{\Delta }}^{(s)}$ 和能力分布${\mathbf{\pi }}^{(s)}$(由M步迭代估计得到)的和观测变量下隐变量的条件分布为：
$\begin{array}{rl}f\left(q_k|{\mathbf{y}}_i,{\Delta }^{(s)},{\pi }^{(s)}\right)& =\frac{f\left({\mathbf{y}}_i|q_k,{\mathbf{\Delta }}^{(s)}\right){\pi }_k^{(s)}}{{\sum }_{k^{\prime }=1}^{K}f\left({\mathbf{y}}_i|q_{k^{\prime }},{\Delta }^{(s)}\right){\pi }_{k^{\prime }}^{(s)}}\\ & =\frac{{\pi }_k^{(s)}{\prod }_{j=1}^{J}P{\left(q_k|{\mathbf{\delta }}_j^{(s)}\right)}^{y_{ij}}{\left[1-P\left(q_k|{\mathbf{\delta }}_j^{(s)}\right)\right]}^{1-y_{ij}}}{{\sum }_{k^{\prime }=1}^K{\pi }_{k^{\prime }}^{(s)}{\prod }_{j=1}^{J}P{\left(q_{k^{\prime }}|{\mathbf{\delta }}_j^{(s)}\right)}^{y_{ij}}{\left[1-P\left(q_{k^{\prime }}|{\mathbf{\delta }}_j^{(s)}\right)\right]}^{1-y_{ij}}}\end{array}$

$n_k^{(s)}=E\left(n_k|\mathbf{Y},{\Delta }^{(s)},{\mathbf{\pi }}^{(s)}\right)={\sum }_{i=1}^{N}f\left(q_k|{\mathbf{y}}_i,{\mathbf{\Delta }}^{(s)},{\mathbf{\pi }}^{(s)}\right)={\sum }_{i=1}^N\frac{f\left({\mathbf{y}}_i|q_k,{\mathbf{\Delta }}^{(s)}\right){\pi }_k^{(s)}}{{\sum }_{k^{\prime }=1}^{K}f\left({\mathbf{y}}_i|q_{k^{\prime }},{\mathbf{\Delta }}^{(s)}\right){\pi }_{k^{\prime }}^{(s)}}={\sum }_{i=1}^N\frac{{\pi }_k^{(s)}{\prod }_{j=1}^{J}P{\left(q_k|{\mathbf{\delta }}_j^{(s)}\right)}^{y_{ij}}{\left[1-P\left(q_k|{\mathbf{\delta }}_j^{(s)}\right)\right]}^{1-y_{ij}}}{{\sum }_{k^{\prime }=1}^K{\pi }_{k^{\prime }}^{(s)}{\prod }_{j=1}^{J}P{\left(q_{k^{\prime }}|{\mathbf{\delta }}_j^{(s)}\right)}^{y_{ij}}{\left[1-P\left(q_{k^{\prime }}|{\mathbf{\delta }}_j^{(s)}\right)\right]}^{1-y_{ij}}}$
$r_{jk}^{(s)}=y_{ij}{n}_k^{(s)}$

M-Step:

M步是使用E步计算的$n_k^{(s)}$和$r_{jk}^{(s)}$去迭代估计$\Delta ,\pi$。根据上述的对数似然函数可得：

$\log \left[L\left({\mathbf{R}}^{(s)},{\mathbf{n}}^{(s)}|\Delta ,\mathbf{\pi }\right)\right]={\sum }_{j=1}^{J}l\left({\mathbf{\delta }}_j\right)+l(\mathbf{\pi })$
其中 $l\left({\mathbf{\delta }}_j\right)={\sum }_{k=1}^K{r}_{jk}^{(s)}\log \left[P\left(q_k|{\mathbf{\delta }}_j\right)\right]+\left(n_k^{(s)}-r_{jk}^{(s)}\right)\log \left[1-P\left(q_k|{\mathbf{\delta }}_j\right)\right]$
$l(\mathbf{\pi })={\sum }_{k=1}^K{n}_k^{(s)}\log \left[{\pi }_k\right]$

使用极大似然估计求$\Delta ,\pi$，由于$\pi$是服从多项式分布的，所以很容易得到

${\pi }_k^{(s+1)}=\frac{n_k^{(s)}}{N}$
为求 $\Delta$，对 $l\left({\mathbf{\delta }}_j\right)$关于 ${\mathbf{\delta }}_j$求导： $\frac{\partial l\left({\mathbf{\delta }}_j\right)}{\partial {\delta }_{tj}}=0$
${\sum }_{k=1}^K\frac{r_{jk}^{(s)}-n_k^{(s)}P\left(q_k|{\mathbf{\delta }}_j\right)}{\left[1-P\left(q_k|{\mathbf{\delta }}_j\right)\right]P\left(q_k|{\mathbf{\delta }}_j\right)}\frac{\partial P\left(q_k|{\mathbf{\delta }}_j\right)}{\partial {\delta }_{tj}}=0$

结果：

使用12000名学生的约100万条做题记录进行IRT参数估计，其中涉及题目约1000道左右，首先使用EM算法对题目参数进行估计，然后使用EAP对学生能力进行估计，结果分别如下：

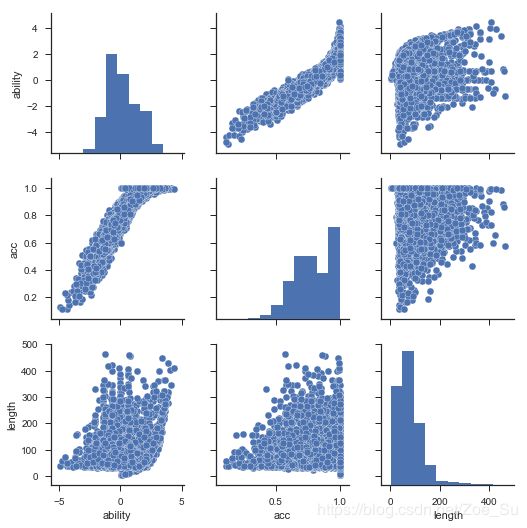
上图中，ability为学生能力对评估结果，acc为学生实际答题的准确率，length为做题记录的长度，从图中可以看出，估计出的学生能力与实际答题的准确率正相关，且估计出的学生能力分布呈正态。相同做题准确率下，不同做题长度对评估结果也有影响。

上图为估计的题目参数，a表示题目的区分度，b表示题目的难度，可以看出题目难度和题目的准确率严格正相关，区分度和准确率呈倒U型。

---

参考文献：

1. http://www.openirt.com/b-a-h/papers/note9801.pdf IRT Parameter Estimation using the EM Algorithm
2. https://zhuanlan.zhihu.com/p/29887184 Python与项目反应理论：基于EM和MCMC的参数估计算法
[3]. https://www.cnblogs.com/jiangxinyang/p/9621997.html IRT模型的参数估计方法（EM算法和MCMC算法）
[4]. https://www.john-uebersax.com/stat/irt2.htm How to Calculate Expected A Posteriori (EAP) Scores for Unidimensional and Multidimensional Latent Trait Models
[5]. https://en.wikipedia.org/wiki/Item_response_theory Item response theory