python求最优解的集中算法
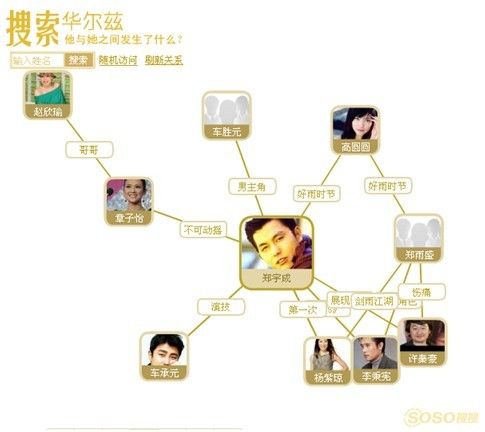
优化算法通常用来处理问题最优解的求解--这个问题有多个变量共同决定的,举一个例子比如有这样一张 人员关系表,需要绘制一张SOSO华尔兹(一种socialnetwork, http://tag.soso.com/),比如:
绘制方法有很多种,我们希望能够最终展现给用户的绘制是比较好阅读的,比如交叉线比较少,每个人的点排的比较开等等。
我们利用以下一个数据格式来描述最终的一个解,即一个向量包含每个人的坐标,假设:通常我们用一个 向量来表示解x, x =[a1,a2,….]
这个矩阵也很多值,那这个绘制方法可能很多,优化算法就是用来寻找和评估其中比较好的一种绘制的结果的解。那这里就要回答一个很关键的问题,什么样的解是好的解,这就需要一个方法来评估一个解的好坏程度,也就是优化算法当中要 定义的 成本函数(Cost Function),在这个案例中就是有一个函数输入是 每个人的坐标,输出是评价这种画法或者说分布质量如何。
常用有4种优化算法:
1 随机搜索
2 爬山法
3 退火法
4 遗传算法
下面该给出各种算法的实现说明,通过程序解释各种求解实现和思想,为了便于理解,先介绍下 数据储存格式:
Python code:
people=['刘翔','姚明','陈道明','郭晶晶','霍启刚','纪伟','罗伯斯','孙海平','史冬鹏','叶莉']
links=[('刘翔', '姚明'),
('刘翔', '陈道明'),
('刘翔', '郭晶晶'),
('刘翔', '纪伟'),
('刘翔', '罗伯斯'),
('刘翔', '孙海平'),
('刘翔', '史冬鹏'),
('姚明', '叶莉'),
('陈道明', '霍启刚'),
('郭晶晶', '霍启刚'),
('纪伟', '罗伯斯'),
('孙海平', '史冬鹏'),
1 随机搜索:主要 依赖于随机函数,每一次求解,都是不确定的变化趋势(更好还是更坏)
#domain 表示解空间,domain
[0] 表示向量x第i个维的最小值,domain[1] 表示向量x第i个维的最大值。
# costf :成本函数(Cost Function)
def randomoptimize(domain,costf):
best=999999999
bestr=None
# 求解 1000次
for i in range(0,1000):
# 创建一个随机的解
r=[float(random.randint(domain
[0],domain[1]))
# 计算 成本
cost=costf(r)
# 是否更优,成本小为更优
if cost
best=cost
bestr=r
return r
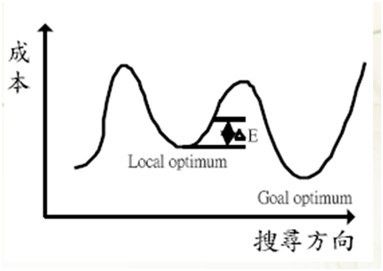
2 爬山法 ,搜索沿着某一个更优方向搜索直到一个极值(如下图的波谷)
以下是python 的一个实现:
#domain 表示解空间,domain
[0] 表示向量x第i个维的最小值,domain[1] 表示向量x第i个维的最大值。
# costf :成本函数(Cost Function)
def hillclimb(domain,costf):
# 从一个随机解开始
sol=[random.randint(domain
[0],domain[1])
#搜索解过程
while 1:
# 每一维都会变化以后现成一个新的解,共有解的长度个邻居解
neighbors=[]
for j in range(len(domain)):
# 解向量 第j维 在解空间,向上或者向下 变化步长1(所以叫邻居解 )
if sol[j]>domain[j][0]:
neighbors.append(sol[0:j]+[sol[j]+1]+sol[j+1:])
if sol[j]
neighbors.append(sol[0:j]+[sol[j]-1]+sol[j+1:])
# 在这一批寻找最优解
current=costf(sol)
best=current
for j in range(len(neighbors)):
cost=costf(neighbors[j])
if cost
best=cost
sol=neighbors[j]
# 当没有更优解出现时候,认为达到某个局部最优解,搜索过程结束
if best==current:
break
return sol
3 退火法
前面的2个优化算法,都是简单往一个更优方向搜索最优解,这样如果遇到下面这种情况,这样很可能陷入一个局部最优解(Local optimum),最终搜索的解可能不是全局最优解(Goal optimum),为了避免这个情况,我们希望搜索过程一定程度允许一些差的解存在,因为这些解很可能存在通往最优解的方向上。
为了实现这个想法,退火法在系统早期允许差解存在,存在概率为P,这个概率越来越小,因为还是要找最优解,所以系统后期基本不接受差的解,这个过程很像 物体退火降温的过程,温度越高时候,分子运动杂乱无章,系统越不稳定,即可以接受差的解,当物体冷却以后,系统趋于稳定,即只接受更优解,我们用这个公式模拟这个过程:
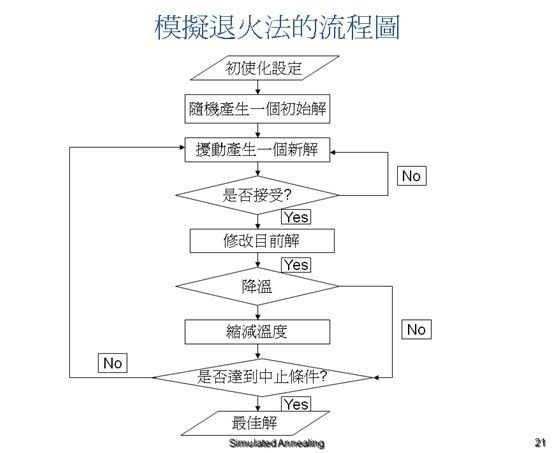
求解过程如下(个人感觉直接看程序 更好理解):
附:模拟退火法( Simulated Annealing;SA) 最早的想法是由N.Metropolis 等人于1953 年所提出,在当时并没有受到重视。直到1983 年由Kirkpatrick et al. 提出蒙地卡罗模拟(MonteCarlo Simulated)概念的随机搜寻技巧,利用此方法来求解的組合最佳化问题时,才使此演算法受到重视。
以下是python 的一个实现:
def annealingoptimize(domain,costf,T=10000.0,cool=0.95,step=1):
# 从一个随机解开始
vec=[float(random.randint(domain
[0],domain[1]))
while T>0.1:
# 随机选择一个维度
i=random.randint(0,len(domain)-1)
# 选择一个搜索方向
dir=random.randint(-step,step)
# 在搜索方向上生成新解
vecb=vec[:]
vecb
+=dir
elif vecb>domain[1]: vecb=domain[1]
ea=costf(vec)
eb=costf(vecb)
#重新计算系统稳定性-概率p,退火算法核心
p=pow(math.e,(-eb-ea)/T)
# 更优解将替换当前解,在系统早期,温度很高,系统很不稳定,非更优解也可能替换当前解,这样做的目的,是避免过快陷入局部最优解,更大范围搜索最优解。
if (eb
vec=vecb
# 减低温度
T=T*cool
return vec
4 遗传算法:这个搜索过程基于一个假设认为全局最优解很可能 存在于当前 最优解种群中的下一代,这个下一代通常由当前最优解种群,通过解空间的某些维的交叉或者变异产生(这里有很多概率:变异范围概率P1,交叉还是变异的概率p2……),新产生的一代中,重新计算成本,保留一定数量最优解,作为当前最优解种群,如此循环经过几代遗传,最终在最后一代最优解种群中选择解。计划这个算法在另外文章中再详细介绍。
为了熟悉这些算法,所以实验了这个案例。除了以上算法,我们还需要编写一个成本函数,这个非常关键,这里列出一种计算方法,通过计算解所描述的图上点之间的距离和线交叉情况,来评估该图分布是否均衡合理(比如:交叉少便于阅读),
代码如下:
def crosscount(v):
loc=dict([(people
,(v[i*2],v[i*2+1])) for i in range(0,len(people))])
total=0
# Loop through every pair of links
for i in range(len(links)):
for j in range(i+1,len(links)):
# 计算线交叉情况
(x1,y1),(x2,y2)=loc[links
[0]],loc[links[1]]
(x3,y3),(x4,y4)=loc[links[j][0]],loc[links[j][1]]
den=(y4-y3)*(x2-x1)-(x4-x3)*(y2-y1)
if den==0: continue
ua=((x4-x3)*(y1-y3)-(y4-y3)*(x1-x3))/den
ub=((x2-x1)*(y1-y3)-(y2-y1)*(x1-x3))/den
if ua>0 and ua<1 and ub>0 and ub<1:
total+=1
#计算点互相的距离
for i in range(len(people)):
for j in range(i+1,len(people)):
(x1,y1),(x2,y2)=loc[people
],loc[people[j]]
dist=math.sqrt(math.pow(x1-x2,2)+math.pow(y1-y2,2))
if dist<50:
total+=(1.0-(dist/50.0))
return total
效果如下:
>>> sol=optimization.annealingoptimize(socialnetwork.domain,socialnetwork.crossc
ount,step=100,cool=0.99)
>>> socialnetwork.crosscount(sol)
总体感觉效果不是很好,这个可能和我们的成本函数也有关,成本函数需要比较好的评价每个解的好与坏。
后来想,是否可以从一个比较好初始状态开始,再利用优化算法进行简单的优化,于是写了一个函数 ,根据人数量,先平均切割块,把关系多的人放在位于中间的联通性比较好的块,这个解作为搜索的初始值:
def init_pos(peoples,height=400):
result =[]
pos_len= round(1+math.sqrt(len(peoples)))
pos_unit=int(height/pos_len)
helf_unit=int(pos_unit/5)
#生成初始位置列表
for i in range(1,pos_len+1):
for j in range(1,pos_len+1):
result.append((pos_weigh(i*pos_unit,j*pos_unit,height),(i*pos_unit-helf_unit,j*pos_unit-helf_unit)))
result.sort()
result.reverse()
#计算每个人的权重
people_weigh={}
for link in links:
people_weigh.setdefault(link[0],0)
people_weigh[link[0]]+=1
people_weigh.setdefault(link[1],0)
people_weigh[link[1]]+=1
people_queue=[]
for item in people_weigh:
people_queue.append((people_weigh[item],item))
people_queue.sort()
people_queue.reverse()
#放置人,根据权重大小先后放置
pos=dict([(people_queue
[1],(result[1])) for i in range(0,len(people_queue))])
pos_values=[]
for i in range(0,len(people)):
pos_values.append(pos[people
][0])
pos_values.append(pos[people][1])
return pos_values
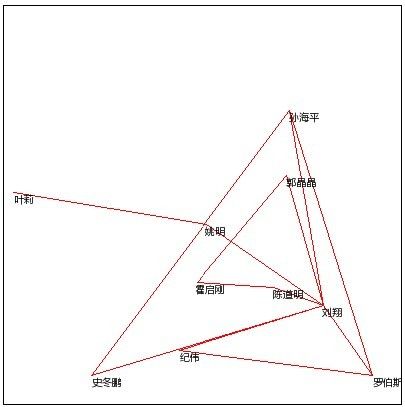
优化的一个结果:
由于时间关系,没有做再多的实验。。。几个算法优化结果都差不多,退火和下山稍微比随机好一点。
总结:
优化算法的一个特点往往给出的是一个局部最优解,不是绝对的最优解,或者说全局最优解。一种优化算法是否有用很大程度取决问题本身,如果问题解本身就是比较无序的,或许随机搜索是最有效的。如以下这种情况,最优解可能位于一个狭小的空间,算法通常很难找到这个最优解的途径,因为任何解决的解成本都很高,都很有可能被排除在外。
那是否能够事先给出一个比较优的初始解,再在这个基础在利用优化算法,是否可以得到较优解,我想可能是存在的,在以上的这个例子当中,我做了下尝试,效果感觉不是很明显,当然也有很有可能是我方法不对。后来分析觉得 实际系统应该是使用类似 mass and spring 算法,这个算法也 模拟自然界中 球和弹簧的运动模型来的:各个节点施力企图远离对方,而节点间的连线又企图拉近其链接的2个节点。
附:
SOSO华尔兹是腾讯(TM)旗下搜索门户SOSO(搜搜)于2009年8月起新增的一项搜索功能。在这个页面里我们可以看到许多明星人物肖像被做成小图标,一个图标所链接的页面就是关于此图片人物的热门关联及其相关热门搜索。
SOSO华尔兹的特点在于:能够把与你要搜索的人物相关的其他人物都连成一个关系网,按照热门程度来进行相关联,您可以在这个页面中发现此人与其相关联人物之间的关系,以及在什么时候发生了什么事情等等。通过点击查看详细,更可以看到关联此事件的网页新闻,博客,搜吧,图片等等。让人非常方便的直接找到关注点以及所关联的人与事。
以上内容是 个人的一些学习笔记,资料大多源于互联网,有很多也是个人的理解,不一定正确,供大家参考。
if vecb[0]: vecb=domain[0]