ML笔记:多类支持向量机损失 Multiclass Support Vector Machine Loss+Python代码实战Mnist数据集!
| 多类支持向量机损失 Multiclass Support Vector Machine Loss+Python代码实战Mnist数据集! |
文章目录
- 一、多类支持向量机损失 Multiclass Support Vector Machine Loss!
- 1.1、损失函数
- 1.2、举例解释
- 1.3、正则化(Regularization)
- 1.4、完整的多类SVM损失
- 1.5、设置 Δ \Delta Δ
- 1.6、梯度推导
- 1.7、Python代码实战Mnist数据集!
- 二、SVM和Softmax的比较
- CNN+L2-SVM分类代码近期公布~~~~~~~~~~~~~~~~
- 参考文献
一、多类支持向量机损失 Multiclass Support Vector Machine Loss!
1.1、损失函数
- SVM的损失函数想要SVM在正确分类上的得分始终比不正确分类上的得分高出一个边界值 Δ \Delta Δ ( Δ \Delta Δ值一般取1,代表间隔),我们可以把损失函数想象成一个人,这位SVM先生(或者女士)对于结果有自己的品位,如果某个结果能使得损失值更低,那么SVM就更加喜欢它。一般而言,深度学习中使用的SVM损失函数是基于Weston and Watkins 1999年提出的Support Vector Machines for Multi-Class Pattern Recognition。首先假设训练数据 ( x 1 , y 1 ) , … , ( x i , y i ) , … , ( x N , y N ) \left(\mathbf{x}_{1}, y_{1}\right), \ldots,\left(\mathbf{x}_{i}, y_{i}\right), \ldots,\left(\mathbf{x}_{N}, y_{N}\right) (x1,y1),…,(xi,yi),…,(xN,yN)有 C C C 个类别, y i ∈ { 1 , ⋯ , C } , ∀ i ∈ { 1 , ⋯ , N } y_{i} \in\{1, \cdots, C\}, \forall i \in\{1, \cdots, N\} yi∈{1,⋯,C},∀i∈{1,⋯,N},针对第 i i i 个数据的多类SVM的损失函数定义如下:
L i = ∑ c = 1 , c ≠ y i C ξ i , c (1) L_{i}=\sum_{c=1, c \neq y_{i}}^{C} \xi_{i, c} \tag{1} Li=c=1,c=yi∑Cξi,c(1) - 即是:
L i = ∑ c ≠ y i max ( 0 , f c − f y i + Δ ) (2) L_{i}=\sum_{c \neq y_{i}} \max \left(0, f_{c}-f_{y_{i}}+\Delta\right)\tag{2} Li=c=yi∑max(0,fc−fyi+Δ)(2) - 在神经网络中,由于我们的评分函数是:
f = w T x + b (3) f=\mathbf{w}^{T} \mathbf{x}+b\tag{3} f=wTx+b(3) - 因此,可以将损失函数改写如下:
L i = ∑ c ≠ y i max ( 0 , w c T x i + b c − w y i T x i − b y i + Δ ) (4) L_{i}=\sum_{c \neq y_{i}} \max \left(0,\mathbf{w}_{c}^{T} x_{i}+b_{c}-\mathbf{w}_{y_{i}}^{T} x_{i}-b_{y_{i}}+\Delta\right)\tag{4} Li=c=yi∑max(0,wcTxi+bc−wyiTxi−byi+Δ)(4)
1.2、举例解释
- 用一个例子演示公式是如何计算的。假设有3个分类,并且得到了分值 f = [ 13 , − 7 , 11 ] f=[13,-7,11] f=[13,−7,11]。其中第1个类别是正确类别,即 y i = 0 y_{i}=0 yi=0。同时假设 Δ \Delta Δ 是10(后面会详细介绍该超参数)。上面的公式是将所有不正确分类 c ≠ y i c \neq y_{i} c=yi 加起来,所以我们得到两个部分:
L i = max ( 0 , − 7 − 13 + 10 ) + max ( 0 , 11 − 13 + 10 ) (5) L_i=\max (0,-7-13+10)+\max (0,11-13+10)\tag{5} Li=max(0,−7−13+10)+max(0,11−13+10)(5) - 可以看到第一个部分结果是0,这是因为 [ − 7 − 13 + 10 ] [-7-13+10] [−7−13+10] 得到的是负数,经过 max ( 0 , − ) \max (0,-) max(0,−) 函数处理后得到0。这一对类别分数和标签的损失值是0,这是因为正确分类的得分13与错误分类的得分-7的差为20,高于边界值10。而SVM只关心差距至少要大于10,更大的差值还是算作损失值为0。第二个部分计算 [ 11 − 13 + 10 ] [11-13+10] [11−13+10] 得到8。虽然正确分类的得分比不正确分类的得分要高(13>11),但是比10的边界值还是小了,分差只有2,这就是为什么损失值等于8。简而言之,SVM的损失函数想要正确分类类别[公式]的分数比不正确类别分数高,而且至少要高 Δ \Delta Δ 。如果不满足这点,就开始计算损失值。
- 还必须提一下的属于是关于0的阀值: max ( 0 , − ) \max (0,-) max(0,−) 函数,它常被称为折叶损失(hinge loss)。有时候会听到人们使用平方折叶损失SVM (即L2-SVM),它使用的是 max ( 0 , − ) 2 \max (0,-)^2 max(0,−)2 将更强烈(平方地而不是线性地)地惩罚过界的边界值。不使用平方是更标准的版本,但是在某些数据集中,平方折叶损失会工作得更好。可以通过交叉验证来决定到底使用哪个。
- 直观理解: 多类SVM“想要”正确类别的分类分数比其他不正确分类类别的分数要高,而且至少高出 Δ \Delta Δ 的边界值。如果其他分类分数进入了红色的区域,甚至更高,那么就开始计算损失。如果没有这些情况,损失值为0。我们的目标是找到一些权重,它们既能够让训练集中的数据样例满足这些限制,也能让总的损失值尽可能地低。

1.3、正则化(Regularization)
- 上面损失函数有一个问题。假设有一个数据集和一个权重集 W \mathbf{W} W 能够正确地分类每个数据(即所有的边界都满足,对于所有的数据 i i i 都有 L i = 0 L_{i}=0 Li=0)。问题在于这个 W \mathbf{W} W 并不唯一:可能有很多相似的 W \mathbf{W} W 都能正确地分类所有的数据。一个简单的例子:如果 W \mathbf{W} W 能够正确分类所有数据,即对于每个数据,损失值都是0。那么当 λ > 1 \lambda>1 λ>1 时,任何数乘 λ W \lambda \mathbf{W} λW 都能使得损失值为0,因为这个变化将所有分值的大小都均等地扩大了,所以它们之间的绝对差值也扩大了。举个例子,如果一个正确分类的分值和举例它最近的错误分类的分值的差距是15,对 W \mathbf{W} W 乘以2将使得差距变成30。
- 换句话直观理解: 我们希望能向某些特定的权重 W \mathbf{W} W 添加一些偏好,对其他权重则不添加,以此来消除模糊性。这一点是能够实现的,方法是向损失函数增加一个正则化惩罚(regularization penalty) R ( W ) R(\mathbf{W}) R(W) 部分。最常用的正则化惩罚是L2范式,L2范式通过对所有参数进行逐元素的平方惩罚来抑制大数值的权重: R ( W ) = ∑ c ∑ l W c , l 2 (6) R(\mathbf{W})=\sum_{c} \sum_{l} \mathbf{W}_{c, l}^{2}\tag{6} R(W)=c∑l∑Wc,l2(6)
- 其中 W = [ w 1 , . . . w C ] \mathbf{W}=[\mathbf{w_1},...\mathbf{w_C}] W=[w1,...wC],故有如下:
R ( W ) = ∑ c = 1 C w c T w c (7) R(\mathbf{W})=\sum_{c=1}^{C} \mathbf{w}_{c}^{T} \mathbf{w}_{c}\tag{7} R(W)=c=1∑CwcTwc(7)
1.4、完整的多类SVM损失
- 上面的表达式中,将 W \mathbf{W} W 中所有元素平方后求和。注意正则化函数不是数据的函数,仅基于权重。包含正则化惩罚后,就能够给出完整的多类SVM损失函数了,它由两个部分组成:数据损失(data loss),即所有样例的的平均损失 L i L_{i} Li,以及正则化损失(regularization loss)。完整公式如下所示: L = 1 N ∑ i L i ⏟ data loss + λ R ( W ) ⏟ regularization loss (8) L=\underbrace{\frac{1}{N} \sum_{i} L_{i}}_{\text {data loss }}+\underbrace{\lambda R(\mathbf{W})}_{\text {regularization loss }}\tag{8} L=data loss N1i∑Li+regularization loss λR(W)(8)
- 将其展开完整公式是:
L = 1 N ∑ i ∑ j ≠ y i [ max ( 0 , w c T x i + b c − w y i T x i − b y i + Δ ) ] + λ ∑ c ∑ l W c , l 2 (9) L=\frac{1}{N} \sum_{i} \sum_{j \neq y_{i}}\left[\max (0,\mathbf{w}_{c}^{T} x_{i}+b_{c}-\mathbf{w}_{y_{i}}^{T} x_{i}-b_{y_{i}}+\Delta\right)]+\lambda \sum_{c} \sum_{l} \mathbf{W}_{c, l}^{2}\tag{9} L=N1i∑j=yi∑[max(0,wcTxi+bc−wyiTxi−byi+Δ)]+λc∑l∑Wc,l2(9) - 其中, N N N 是训练集的数据量。现在正则化惩罚添加到了损失函数里面,并用超参数 λ \lambda λ 来计算其权重。该超参数无法简单确定,需要通过交叉验证来获取。引入正则化惩罚其中最好的性质就是对大数值权重进行惩罚,可以提升其泛化能力,因为这就意味着没有哪个维度能够独自对于整体分值有过大的影响。举个例子,假设输入向量 x = [ 1 , 1 , 1 , 1 ] \mathbf{x}=[1,1,1,1] x=[1,1,1,1],两个权重向量 w 1 = [ 1 , 0 , 0 , 0 ] \mathbf{w}_{1}=[1,0,0,0] w1=[1,0,0,0], w 2 = [ 0.25 , 0.25 , 0.25 , 0.25 ] \mathbf{w}_{2}=[0.25,0.25,0.25,0.25] w2=[0.25,0.25,0.25,0.25]。那么 w 1 T x = w 2 T x = 1 \mathbf{w}_{1}^{T}\mathbf{x}=\mathbf{w}_{2}^{T}\mathbf{x}=1 w1Tx=w2Tx=1,两个权重向量都得到同样的内积,但是 w 1 \mathbf{w}_{1} w1 的L2惩罚是1.0,而 w 2 \mathbf{w}_{2} w2 的L2惩罚是0.25。因此,根据L2惩罚来看, w 1 \mathbf{w}_{1} w1 更好,因为它的正则化损失更小。从直观上来看,这是因为 w 1 \mathbf{w}_{1} w1 的权重值更小且更分散。既然L2惩罚倾向于更小更分散的权重向量,这就会鼓励分类器最终将所有维度上的特征都用起来,而不是强烈依赖其中少数几个维度。在后面的课程中可以看到,这一效果将会提升分类器的泛化能力,并避免过拟合。
- 另外需要注意的是,和权重不同,偏差没有这样的效果,因为它们并不控制输入维度上的影响强度。因此通常只对权重 W \mathbf{W} W 正则化,而不正则化偏差 b b b 。在实际操作中,可发现这一操作的影响可忽略不计。最后,因为正则化惩罚的存在,不可能在所有的例子中得到0的损失值,这是因为只有当 W = 0 \mathbf{W}=0 W=0 的特殊情况下,才能得到损失值为0。
- 注意:一般我们在论文中所见到的多类SVM目标函数为如下
min w c , b , ξ 1 2 ∑ c = 1 C w c T w c + θ ∑ i = 1 N ∑ c = 1 , c ≠ y i C ξ i , c (10) \min _{w_{c}, b, \xi} \frac{1}{2} \sum_{c=1}^{C} \mathbf{w}_{c}^{T} \mathbf{w}_{c}+\theta \sum_{i=1}^{N} \sum_{c=1, c \neq y_{i}}^{C} \xi_{i, c} \tag{10} wc,b,ξmin21c=1∑CwcTwc+θi=1∑Nc=1,c=yi∑Cξi,c(10) - 可以写成如下:
min w c , b 1 2 ∑ c = 1 C w c T w c + θ ∑ i = 1 N ∑ c = 1 , c ≠ y i C max ( 0 , f c − f y i + Δ ) (11) \min _{w_{c}, b} \frac{1}{2} \sum_{c=1}^{C} \mathbf{w}_{c}^{T} \mathbf{w}_{c}+\theta \sum_{i=1}^{N} \sum_{c=1, c \neq y_{i}}^{C} \max \left(0, f_{c}-f_{y_{i}}+\Delta\right)\tag{11} wc,bmin21c=1∑CwcTwc+θi=1∑Nc=1,c=yi∑Cmax(0,fc−fyi+Δ)(11) - 因此,可以将损失函数改写如下:
min w c , b c 1 2 ∑ c = 1 C w c T w c + θ ∑ i = 1 N ∑ c = 1 , c ≠ y i C max ( 0 , w c T x i + b c − w y i T x i − b y i + Δ ) (12) \min _{w_{c}, b_{c}} \frac{1}{2} \sum_{c=1}^{C} \mathbf{w}_{c}^{T} \mathbf{w}_{c}+\theta \sum_{i=1}^{N} \sum_{c=1, c \neq y_{i}}^{C} \max \left(0,\mathbf{w}_{c}^{T} x_{i}+b_{c}-\mathbf{w}_{y_{i}}^{T} x_{i}-b_{y_{i}}+\Delta\right)\tag{12} wc,bcmin21c=1∑CwcTwc+θi=1∑Nc=1,c=yi∑Cmax(0,wcTxi+bc−wyiTxi−byi+Δ)(12)
1.5、设置 Δ \Delta Δ
- 你可能注意到上面的内容对超参数 Δ \Delta Δ 及其设置是一笔带过,那么它应该被设置成什么值?需要通过交叉验证来求得吗?现在看来,该超参数在绝大多数情况下设为 Δ = 1.0 \Delta=1.0 Δ=1.0 都是安全的。超参数 Δ \Delta Δ 和 λ \lambda λ 看起来是两个不同的超参数,但实际上他们一起控制同一个权衡:即损失函数中的数据损失和正则化损失之间的权衡。理解这一点的关键是要知道,权重 W \mathbf{W} W 的大小对于分类分值有直接影响(当然对他们的差异也有直接影响):当我们将 W \mathbf{W} W 中值缩小,分类分值之间的差异也变小,反之亦然。因此,不同分类分值之间的边界的具体值(比如 Δ = 1 \Delta=1 Δ=1 或者 Δ = 100 \Delta=100 Δ=100)从某些角度来看是没意义的,因为权重自己就可以控制差异变大和缩小。也就是说,真正的权衡是我们允许权重能够变大到何种程度(通过正则化强度 λ \lambda λ 来控制)。
1.6、梯度推导
-
矩阵 W \mathbf{W} W 代表权值,维度是 D ∗ C D∗C D∗C,其中 D D D代表特征的维度, C C C 代表类别数目。
-
矩阵 X \mathbf{X} X 代表样本集合,维度是 N ∗ D N∗D N∗D, 其中 N N N 代表样本个数。
-
分值计算公式为 f = X f=\mathbf{X} f=X∗ W \mathbf{W} W,其维度为 N ∗ C N∗C N∗C, 每行代表一个样本的不同类别的分值。
-
对于第 i i i 个样本的损失函数(这里没有正则项)计算如下:
L i = ∑ c ≠ y i max ( 0 , W : , c T x i , : − W : , y i T x i , : + Δ ) (13) L_{i}=\sum_{c \neq y_{i}} \max \left(0, \mathbf{W}_{ :, c}^{T} x_{i, :}-\mathbf{W}_{ :, y_{i}}^{T} x_{i, :}+\Delta\right)\tag{13} Li=c=yi∑max(0,W:,cTxi,:−W:,yiTxi,:+Δ)(13) -
偏导数计算如下:
∂ L i ∂ W : , y i = − ( ∑ c ≠ y i 1 ( w : , c T x i , i − w : y i T x i , i + Δ > 0 ) ) x i , : (14) \frac{\partial L_{i}}{\partial \mathbf{W}_{ :, y_{i}}}=-\left(\sum_{c \neq y_{i}} 1\left(\mathbf{w}_{ :, c}^{T} x_{i, i}-\mathbf{w}_{ : y_{i}}^{T} x_{i, i}+\Delta>0\right)\right) x_{i, :}\tag{14} ∂W:,yi∂Li=−⎝⎛c=yi∑1(w:,cTxi,i−w:yiTxi,i+Δ>0)⎠⎞xi,:(14) -
同时 ∂ L i ∂ W : , c = 1 ( w : , c T x i , : − w : , y i T x i , : + Δ > 0 ) x i , : (15) \frac{\partial L_{i}}{\partial \mathbf{W}_{ :, c}}=1\left(\mathbf{w}_{ :, c}^{T} x_{i, :}-\mathbf{w}_{ :, y_{i}}^{T} x_{i, :}+\Delta>0\right) x_{i, :}\tag{15} ∂W:,c∂Li=1(w:,cTxi,:−w:,yiTxi,:+Δ>0)xi,:(15)
-
其中:
- w : , c \mathbf{w}_{ :, c} w:,c 代表 W \mathbf{W} W 矩阵第 c c c 列,其维度为 D D D。
- x i , : x_{i, :} xi,: 代表 X \mathbf{X} X 矩阵的第 i i i 行,表示样本 i i i 的特征,其维度也为 D D D 。
- w : , c T x i , : \mathbf{w}_{ :, c}^{T}x_{i, :} w:,cTxi,:二者相乘,得出的是样本 i i i 在第 c c c 个类别上的得分。
- 1 1 1 代表示性函数。
1.7、Python代码实战Mnist数据集!
- 训练数据获取地址:链接+提取码582f
- 完整版代码如下:
from __future__ import division
import numpy as np
"""
@author: Devinzhang 2019-10-01
This dataset is part of MNIST dataset,but there is only 3 classes,
classes = {0:'0',1:'1',2:'2'},and images are compressed to 14*14
pixels and stored in a matrix with the corresponding label, at the
end the shape of the data matrix is
num_of_images x 14*14(pixels)+1(lable)
"""
def load_data(split_ratio):
tmp=np.load("data.npy")
data=tmp[:,:-1]
label=tmp[:,-1]
mean_data=np.mean(data,axis=0)
train_data=data[int(split_ratio*data.shape[0]):]-mean_data
train_label=label[int(split_ratio*data.shape[0]):]
test_data=data[:int(split_ratio*data.shape[0])]-mean_data
test_label=label[:int(split_ratio*data.shape[0])]
return train_data,train_label,test_data,test_label
"""compute the hingle loss without using vector operation,
While dealing with a huge dataset,this will have low efficiency
X's shape [n,14*14+1],Y's shape [n,],W's shape [num_class,14*14+1]"""
def lossAndGradNaive(X,Y,W,reg):
dW=np.zeros(W.shape)
loss = 0.0
num_class=W.shape[0]
num_X=X.shape[0]
for i in range(num_X):
scores=np.dot(W,X[i])
cur_scores=scores[int(Y[i])]
for j in range(num_class):
if j==Y[i]:
continue
margin=scores[j]-cur_scores+1
if margin>0:
loss+=margin
dW[j,:]+=X[i]
dW[int(Y[i]),:]-=X[i]
loss/=num_X
dW/=num_X
loss+=reg*np.sum(W*W)
dW+=2*reg*W
return loss,dW
def lossAndGradVector(X,Y,W,reg):
dW=np.zeros(W.shape)
N=X.shape[0]
Y_=X.dot(W.T)
margin=Y_-Y_[range(N),Y.astype(int)].reshape([-1,1])+1.0
margin[range(N),Y.astype(int)]=0.0
margin=(margin>0)*margin
loss=0.0
loss+=np.sum(margin)/N
loss+=reg*np.sum(W*W)
"""For one data,the X[Y[i]] has to be substracted several times"""
countsX=(margin>0).astype(int)
countsX[range(N),Y.astype(int)]=-np.sum(countsX,axis=1)
dW+=np.dot(countsX.T,X)/N+2*reg*W
return loss,dW
def predict(X,W):
X=np.hstack([X, np.ones((X.shape[0], 1))])
Y_=np.dot(X,W.T)
Y_pre=np.argmax(Y_,axis=1)
return Y_pre
def accuracy(X,Y,W):
Y_pre=predict(X,W)
acc=(Y_pre==Y).mean()
return acc
def model(X,Y,alpha,steps,reg):
X=np.hstack([X, np.ones((X.shape[0], 1))])
W = np.random.randn(3,X.shape[1]) * 0.0001
for step in range(steps):
loss,grad=lossAndGradNaive(X,Y,W,reg)
W-=alpha*grad
print("The {} step, loss={}, accuracy={}".format(step,loss,accuracy(X[:,:-1],Y,W)))
return W
train_data,train_label,test_data,test_label=load_data(0.2)
W=model(train_data,train_label,0.0001,25,0.5)
print("Test accuracy of the model is {}".format(accuracy(test_data,test_label,W)))
- 实验结果
ssh://[email protected]:22/home/zhangkf/anaconda3/envs/tf2c/bin/python -u /home/zhangkf/tf/TF1/svm_test/SVM_Version1.py
The 0 step, loss=1.9669065288495866, accuracy=0.9075144508670521
The 1 step, loss=0.5496390813958856, accuracy=0.9248554913294798
The 2 step, loss=0.42061570363890477, accuracy=0.9364161849710982
The 3 step, loss=0.3262427878538634, accuracy=0.9421965317919075
The 4 step, loss=0.2702680562078132, accuracy=0.9595375722543352
The 5 step, loss=0.21727828871056154, accuracy=0.9653179190751445
The 6 step, loss=0.16696083041345366, accuracy=0.9710982658959537
The 7 step, loss=0.1301956858983133, accuracy=0.9826589595375722
The 8 step, loss=0.1055701823919878, accuracy=0.9826589595375722
The 9 step, loss=0.08860423223431467, accuracy=0.9884393063583815
The 10 step, loss=0.07615233446374876, accuracy=0.9884393063583815
The 11 step, loss=0.06636955383351115, accuracy=0.9884393063583815
The 12 step, loss=0.06109815579247061, accuracy=0.9884393063583815
The 13 step, loss=0.05525243126969201, accuracy=0.9884393063583815
The 14 step, loss=0.04872271524678853, accuracy=0.9884393063583815
The 15 step, loss=0.04280360346485378, accuracy=0.9884393063583815
The 16 step, loss=0.036075227483702635, accuracy=0.9884393063583815
The 17 step, loss=0.03085022739599956, accuracy=0.9884393063583815
The 18 step, loss=0.024139528055343917, accuracy=0.9942196531791907
The 19 step, loss=0.017860570111603725, accuracy=0.9942196531791907
The 20 step, loss=0.013240863121183073, accuracy=0.9942196531791907
The 21 step, loss=0.00984510428960199, accuracy=1.0
The 22 step, loss=0.007724562778701633, accuracy=1.0
The 23 step, loss=0.00481805318548185, accuracy=1.0
The 24 step, loss=0.0029332622896068253, accuracy=1.0
Test accuracy of the model is 0.9767441860465116
Process finished with exit code 0
- 附加补充1: 包括向量化版本和非向量化版本:
def svm_loss_naive(W, X, y, reg):
"""
# SVM 损失函数 native版本
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
dW = np.zeros(W.shape) # initialize the gradient as zero
# compute the loss and the gradient
num_classes = W.shape[1]
num_train = X.shape[0]
loss = 0.0
# 对于每一个样本,累加loss
for i in xrange(num_train):
scores = X[i].dot(W) # (1, C)
correct_class_score = scores[y[i]]
for j in xrange(num_classes):
if j == y[i]:
continue
# 根据 SVM 损失函数计算
margin = scores[j] - correct_class_score + 1 # note delta = 1
# 当 margin>0 时,才会有损失,此时也会有梯度的累加
if margin > 0: # max(0, yi - yc + 1)
loss += margin
# 根据公式:∇Wyi Li = - xiT(∑j≠yi1(xiWj - xiWyi +1>0)) + 2λWyi
dW[:, y[i]] += -X[i, :] # y[i] 是正确的类
# 根据公式: ∇Wj Li = xiT 1(xiWj - xiWyi +1>0) + 2λWj ,
dW[:, j] += X[i, :]
# 训练数据平均损失
loss /= num_train
dW /= num_train
# 正则损失
loss += 0.5 * reg * np.sum(W * W)
dW += reg * W
return loss, dW
def svm_loss_vectorized(W, X, y, reg):
"""
SVM 损失函数 向量化版本
Structured SVM loss function, vectorized implementation.Inputs and outputs
are the same as svm_loss_naive.
"""
loss = 0.0
dW = np.zeros(W.shape) # initialize the gradient as zero
scores = X.dot(W) # N by C 样本数*类别数
num_train = X.shape[0]
num_classes = W.shape[1]
scores_correct = scores[np.arange(num_train), y]
scores_correct = np.reshape(scores_correct, (num_train, 1)) # N*1 每个样本的正确类别
margins = scores - scores_correct + 1.0 # N by C 计算scores矩阵中每一处的损失
margins[np.arange(num_train), y] = 0.0 # 每个样本的正确类别损失置0
margins[margins <= 0] = 0.0 # max(0, x)
loss += np.sum(margins) / num_train # 累加所有损失,取平均
loss += 0.5 * reg * np.sum(W * W) # 正则
# compute the gradient
margins[margins > 0] = 1.0 # max(0, x) 大于0的梯度计为1
row_sum = np.sum(margins, axis=1) # N*1 每个样本累加
margins[np.arange(num_train), y] = -row_sum # 类正确的位置 = -梯度累加
dW += np.dot(X.T, margins)/num_train + reg * W # D by C
return loss, dW
- 附加补充2: 包括向量化版本和非向量化版本:
def L_i(x, y, W):
"""
unvectorized version. Compute the multiclass svm loss for a single example (x,y)
- x is a column vector representing an image (e.g. 3073 x 1 in CIFAR-10)
with an appended bias dimension in the 3073-rd position (i.e. bias trick)
- y is an integer giving index of correct class (e.g. between 0 and 9 in CIFAR-10)
- W is the weight matrix (e.g. 10 x 3073 in CIFAR-10)
"""
delta = 1.0 # see notes about delta later in this section
scores = W.dot(x) # scores becomes of size 10 x 1, the scores for each class
correct_class_score = scores[y]
D = W.shape[0] # number of classes, e.g. 10
loss_i = 0.0
for j in xrange(D): # iterate over all wrong classes
if j == y:
# skip for the true class to only loop over incorrect classes
continue
# accumulate loss for the i-th example
loss_i += max(0, scores[j] - correct_class_score + delta)
return loss_i
def L_i_vectorized(x, y, W):
"""
A faster half-vectorized implementation. half-vectorized
refers to the fact that for a single example the implementation contains
no for loops, but there is still one loop over the examples (outside this function)
"""
delta = 1.0
scores = W.dot(x)
# compute the margins for all classes in one vector operation
margins = np.maximum(0, scores - scores[y] + delta)
# on y-th position scores[y] - scores[y] canceled and gave delta. We want
# to ignore the y-th position and only consider margin on max wrong class
margins[y] = 0
loss_i = np.sum(margins)
return loss_i
def L(X, y, W):
"""
fully-vectorized implementation :
- X holds all the training examples as columns (e.g. 3073 x 50,000 in CIFAR-10)
- y is array of integers specifying correct class (e.g. 50,000-D array)
- W are weights (e.g. 10 x 3073)
"""
# evaluate loss over all examples in X without using any for loops
# left as exercise to reader in the assignment
二、SVM和Softmax的比较
- 精确地说,SVM分类器使用的是折叶损失(hinge loss),有时候又被称为最大边界损失(max-margin loss)。Softmax分类器使用的是交叉熵损失(corss-entropy loss)。Softmax分类器的命名是从softmax函数那里得来的,softmax函数将原始分类评分变成正的归一化数值,所有数值和为1,这样处理后交叉熵损失才能应用。注意从技术上说“softmax损失(softmax loss)”是没有意义的,因为softmax只是一个压缩数值的函数。但是在这个说法常常被用来做简称。
- 下图有助于区分这 Softmax和SVM这两种分类器:
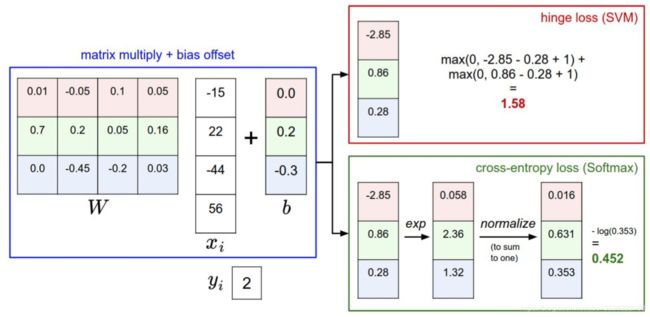
- 针对一个数据点,SVM和Softmax分类器的不同处理方式的例子。两个分类器都计算了同样的分值向量 f f f(本节中是通过矩阵乘来实现)。不同之处在于对f中分值的解释:SVM分类器将它们看做是分类评分,它的损失函数鼓励正确的分类(本例中是蓝色的类别2)的分值比其他分类的分值高出至少一个边界值。Softmax分类器将这些数值看做是每个分类没有归一化的对数概率,鼓励正确分类的归一化的对数概率变高,其余的变低。SVM的最终的损失值是1.58,Softmax的最终的损失值是0.452,但要注意这两个数值没有可比性。只在给定同样数据,在同样的分类器的损失值计算中,它们才有意义。
- Softmax分类器为每个分类提供了“可能性”: SVM的计算是无标定的,而且难以针对所有分类的评分值给出直观解释。Softmax分类器则不同,它允许我们计算出对于所有分类标签的可能性。举个例子,针对给出的图像,SVM分类器可能给你的是一个 [ 12.5 , 0.6 , − 23.0 ] [12.5, 0.6, -23.0] [12.5,0.6,−23.0] 对应分类“猫”,“狗”,“船”。而softmax分类器可以计算出这三个标签的”可能性“是 [ 0.9 , 0.09 , 0.01 ] [0.9, 0.09, 0.01] [0.9,0.09,0.01],这就让你能看出对于不同分类准确性的把握。为什么我们要在”可能性“上面打引号呢?这是因为可能性分布的集中或离散程度是由正则化参数λ直接决定的, λ \lambda λ 是你能直接控制的一个输入参数。举个例子,假设3个分类的原始分数是 [ 1 , − 2 , 0 ] [1, -2, 0] [1,−2,0],那么softmax函数就会计算: [ 1 , − 2 , 0 ] → [ e 1 , e − 2 , e 0 ] = [ 2.71 , 0.14 , 1 ] → [ 0.7 , 0.04 , 0.26 ] [1,-2,0] \rightarrow\left[e^{1}, e^{-2}, e^{0}\right]=[2.71,0.14,1] \rightarrow[0.7,0.04,0.26] [1,−2,0]→[e1,e−2,e0]=[2.71,0.14,1]→[0.7,0.04,0.26]
- 现在,如果正则化参数 λ \lambda λ 更大,那么权重 W \mathbf{W} W 就会被惩罚的更多,然后他的权重数值就会更小。这样算出来的分数也会更小,假设小了一半吧 [ 0.5 , − 1 , 0 ] [0.5, -1, 0] [0.5,−1,0],那么softmax函数的计算就是: [ 0.5 , − 1 , 0 ] → [ e 0.5 , e − 1 , e 0 ] = [ 1.65 , 0.73 , 1 ] → [ 0.55 , 0.12 , 0.33 ] [0.5,-1,0] \rightarrow\left[e^{0.5}, e^{-1}, e^{0}\right]=[1.65,0.73,1] \rightarrow[0.55,0.12,0.33] [0.5,−1,0]→[e0.5,e−1,e0]=[1.65,0.73,1]→[0.55,0.12,0.33]
- 现在看起来,概率的分布就更加分散了。还有,随着正则化参数λ不断增强,权重数值会越来越小,最后输出的概率会接近于均匀分布。这就是说,softmax分类器算出来的概率最好是看成一种对于分类正确性的自信。和SVM一样,数字间相互比较得出的大小顺序是可以解释的,但其绝对值则难以直观解释。
- 在实际使用中,SVM和Softmax经常是相似的: 通常说来,两种分类器的表现差别很小,不同的人对于哪个分类器更好有不同的看法。相对于Softmax分类器,SVM更加“局部目标化(local objective)”,这既可以看做是一个特性,也可以看做是一个劣势。考虑一个评分是[10, -2, 3]的数据,其中第一个分类是正确的。那么一个SVM( Δ = 1 \Delta=1 Δ=1)会看到正确分类相较于不正确分类,已经得到了比边界值还要高的分数,它就会认为损失值是0。SVM对于数字个体的细节是不关心的:如果分数是 [ 10 , − 100 , − 100 ] [10, -100, -100] [10,−100,−100] 或者 [ 10 , 9 , 9 ] [10, 9, 9] [10,9,9],对于SVM来说没设么不同,只要满足超过边界值等于1,那么损失值就等于0。
- 对于softmax分类器,情况则不同。对于[10, 9, 9]来说,计算出的损失值就远远高于[10, -100, -100]的。换句话来说,softmax分类器对于分数是永远不会满意的:正确分类总能得到更高的可能性,错误分类总能得到更低的可能性,损失值总是能够更小。但是,SVM只要边界值被满足了就满意了,不会超过限制去细微地操作具体分数。这可以被看做是SVM的一种特性。举例说来,一个汽车的分类器应该把他的大量精力放在如何分辨小轿车和大卡车上,而不应该纠结于如何与青蛙进行区分,因为区分青蛙得到的评分已经足够低了。
CNN+L2-SVM分类代码近期公布~~~~~~~~~~~~~~~~
参考文献
- 这里主要参考了以下作者,表示感谢!
- 深度学习CV】SVM, Softmax损失函数
- CS231n课程笔记翻译:线性分类笔记(中,下)包括损失函数的内容