树的旋转详解
以AVL树为例讲解树的旋转,包教包会——完全掌握并且透彻理解!
概述
AVL树适合讲解树的旋转(实际上树的旋转就是以AVL为原型讲的),不仅因为它高度平衡,更因为它的旋转高度自调整算法是调用在每次AVL树的平衡被打破之时,换句话说,AVL树的旋转是被动的(伺机而动)
由于AVL是查找树,而我们通常(其实已经成了一个惯例、潜规则)插入元素时把它插到叶子结点的位置(先判断,直到NULL找到窝点开始插入)
既然插入位置都限制死掉了这样也省得讨论(我是说『中间结点』,不存在的啊)了,我们说当一个新元素被强行插到一棵AVL树中,存在以下几种情况:
0)仍然平衡(这个我们不考虑)
1)RR型
2)LL型
3)RL型
4)LR型
看到上面四点类型,要在你的神经通路里建立一个反射弧:『RR型』和『LL型』互为镜像,『RL型』和『LR型』互为镜像;『RL型』和『LR型』可以通过一次旋转划归为『RR型』和『LL型』——要像诵经一样,建立一个长久而不衰退的运动型记忆,这样以后看到类似的问题就知道『哦这个我们以前看过的,应该是这四类类型的xx类型』,这样距离成功就又近了一半
详解
本着『简单即是美德』,我将省略作为镜像的『LL型』和『LR型』
P.s. 以下转轴结点是指失衡发生的结点
RR型
所谓『RR型』是指『插入结点是转轴结点右孩子的右孩子』,放心,失衡其实影响的『范围』还是比较小的(『转轴的右孩子的右孩子』,看来也只是『四层』的感觉),虽然实际操作中会涉及到不止四层树高但是我们只关注『转轴的位置』和『旋转的方向』我们说这里四层就够了,看实例:
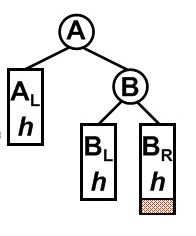
为了方便描述,我们用『圆点』表示『结点』,而用『方框』(有经验的同学肯定还看过用三角形表示的)表示『子树』,就是『一群结点』
可以看到,当我们在A的Right侧(R)的Right侧(R)插入一个新的结点(不晓得是哪个反正就插在『Br子树或者说结点群』之中)
根据定义(复习『平衡』的定义,要会背!形成反射弧!既可以从『结点高度』这个基本定义出发,也可以从平衡因子BF的角度考虑二者本质是一样的而且考虑到最后计算的是差值所以实际上我们并不关系实际大小,我们只关心『在插入操作后,是否存在这样的结点,它满足:该结点的左子树高度减去右子树高度等于2』,为什么是2,因为我们插入是一个一个的插进去的,而我们说『AVL树是高度平衡的自平衡二叉查找树』,在失衡之前(直到上一次失衡那是上一次的事情,我们不管)都是平衡的,故如果要失衡,该失衡结点的BF必然是从-1、0、1(中间可能还有摆动比如-1、0、0、0、1、0、-1、0……当然可能没有-1但是如果数据足够大我们完全可以认为这样的假设是合理的)一步步(每次自增+1)逼近『2』的——红色的字体完全可以写一个函数进行条件判断为下一步的『变形』做铺垫,所谓变形就是旋转
现在你终于理解为什么会『失衡』(看上图),因为我们把新的元素插入到『Br子树』后,向上回溯发现结点A的BF变成了2——不放心再看一遍上面一段文字确认无误后断言:『因为新结点的插入到A的R子树的R侧,导致了以A为树根的树(整个查找树的子树,初中力学『先局部后整体』的思想)失衡进而连锁导致整棵查找树的失衡(真是一粒老鼠屎坏了一锅粥啊)』
现在我们为了重新使整棵查找树平衡,抓住问题矛盾的要害是不是就是要让局部失衡的子树,也就是以A为树根的树调整平衡?当然。
我帮你理清一下思路:
插入新结点到Br子树 => 以A为树根的树失衡 => 整棵树失衡现在要重新平衡整棵树,还是采取先局部后整体的方法:
整棵树要重新平衡 => 以A为树根的树要平衡 => ???上面『???』就是用来『抵消』插入新结点造成的影响的
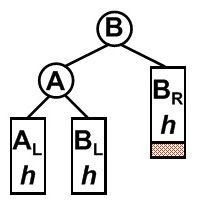
我们本着实用主义,直接告诉你以后看到这样的情形——什么话也不要讲,果断这样做就好了『把最小不平衡树(就是以A为树根的树)绕着树根也就是所谓的转轴逆时针旋转(也叫左旋),直到重新达到平衡』
至于具体操作,你可以把『转轴』(失衡结点)想象成一个『把手』(才不是物理上圆周运动的『转轴』,人家那是『绕着』它转,这里是『拎着』它转,坑爹的翻译啊——准确说,RL、LR类型的所谓『转轴』在第一次旋转时才和物理上的转轴是一个概念)
于是你『拎着』这个失衡的结点,把它逆时针旋转,转过了水平线,直到……
你说你没看明白,那我给你看一遍慢动作版的:
0x01)新结点『10』(姑且用结点的值表示该结点)入侵,找到据点和『8』怼上了,在插入操作后例行检查『判断是否存在失衡根结点』——找到,结点『5』的左子树高1,而右子树却高3,相差为『2』(之前说过,2是一个神奇的数字),于是你的反射弧起作用了——找到所谓的转轴『5』,拎着它逆时针转过水平线,结点『5』下降,结点『7』上升(这就是所谓的连锁效应,整个二叉树不就是一个联动装置吗?!)
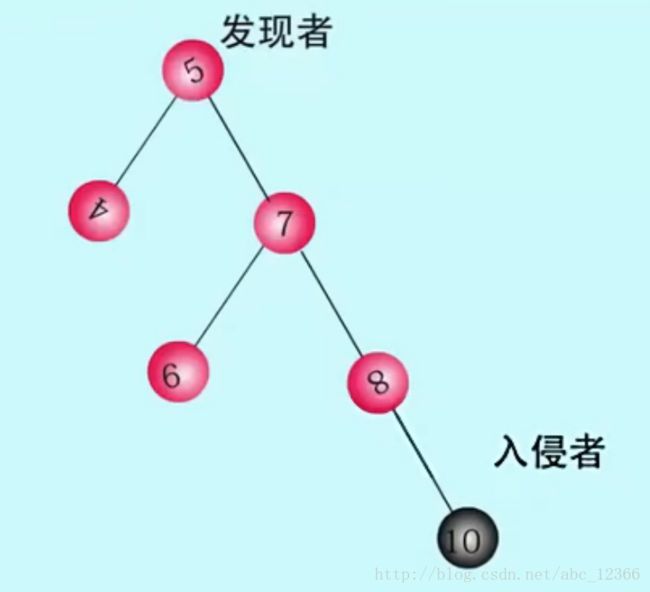
0x02)原来如此(你恍然大悟),结点之间看不见的『连线』不就是所谓的传导力(『传导』不严谨,但是大家懂就好了)的装置吗(好不扯远了)。这里有一个细节:当结点『5』绕下来时『5』和『6』重合——从『7』的视角看『5』和『6』是一样的,对此我们给出的解决方案是『把结点5搞成7的结点,是的连锁效应原来5的孩子4现在变成了7的孙子』(为什么要这样搞?我们给出的解释是,还是从物理角度出发你是不是觉得这样安排整体看最『稳定』、最『和谐』?是的。其实你真的用几个小球模拟实验,也会得出这样的结果,打住不扯远了。)
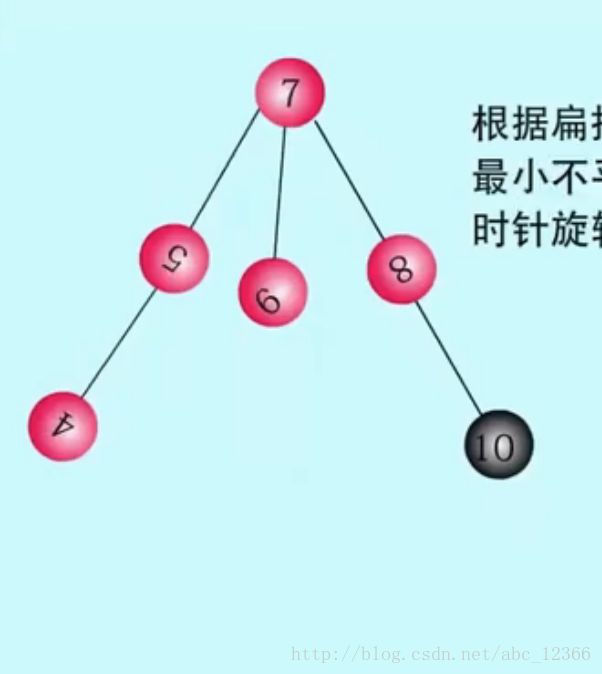
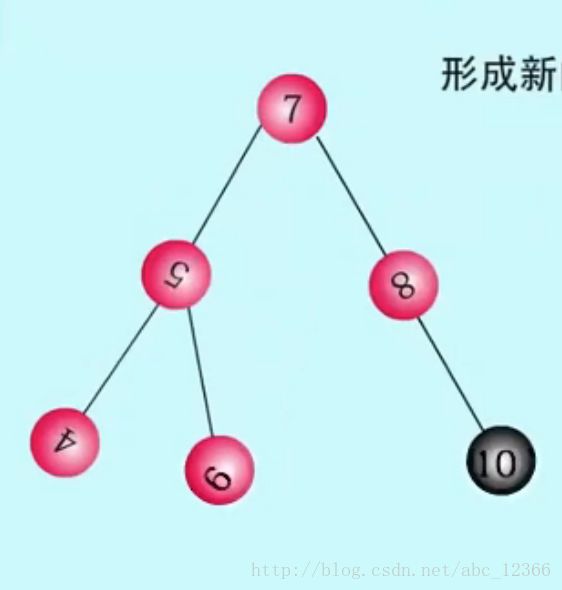
0x03)上一步结束时,结点『7』有了三个孩子,而我们说『一棵AVL树首先是二叉树,二叉树每个结点的孩子是不允许多于2个的』——嗯,看来有一个孩子是假孩子(寄住在结点『7』家里的孩子)——我说『这个假孩子就是结点6你知道吗』——我是怎么知道的?很简单:还是那句话(紧抓定义!),因为AVL不管怎么转它永远都是一棵查找树,而查找树的特点是什么(如果考虑时间超过1秒说明你不熟练,该回去复习概念了)?作为一棵查找树:1)每个结点两个孩子结点,一个左孩子、一个右孩子,2)其中左孩子比该结点大,右孩子比该结点小(排序起来就是:左孩子 > 当前结点 > 右孩子)。既然这样,要做的似乎很明确了——把不和谐的『中间者』(6介于5和8之间)从当前层剔除并下移一层(为什么移到左边?这和具体操作有关,如果刚刚降下来的是右边就移到右边——这样肯定是出于方便写代码的角度考虑的,你想啊旋转下来肯定要占用代码行的吧,肯定有指代的吧,那我们何不顺水推舟做一个顺势人情把多出来的『6』推到刚刚降下来的『5』下面作为它的孩子呢?)
RL型
有了『RR型』的铺垫,要理解『RL型』已经是呼之欲出的事情了
0x01)插入结点『13』(姑且用结点的数据表示该结点),向上回溯(为什么向上回溯?因为人家本来就是靠潜规则强行插到叶子结点的位置的,人家下面没人了啊,总不能向下回溯NULL搞一身劲吧)

0x02)真是毫不费力就找到第一个失衡的结点(根据『局部和整体的关系』往上肯定都是不平衡的),叫结点『10』——这时候你忍不住回头又看了一眼上面的具体操作『用手拎着失衡结点,转动……』咦,刚刚讲的玩意怎不管用了?你想呢。(帮你想:拎着『10』转过水平线,『10』似乎成了『14』的孩子……但是!『12』~『13』这条路径太长了,大于一个结点了!还是太深!我们有RR的经验,完全可以打断连接结点的细绳,然后把哪个结点下移一层……但是!那仅仅是针对一个结点而言!这里有『12』、『13』两个结点,所以不行!)看来我们有必要针对这种新型构型搞出一套新的方案:一个最单纯的想法是『划归』,通俗讲就是『未知问题已知化』,操作起来就是『以结点14为转轴,拎着顺指针转动……进过一系列操作后问题自然划归为RR类型——相当于旋转了两次,第一次是为了第二次做铺垫』。讲起来简单,这里有两个问题要解释:1)为什么绕着结点『14』?我可以敷衍的说『因为结点14是失衡结点10的右孩子,书上就是这么讲的』,其实这里『12』不仅可以看成是『失衡结点10的右孩子』,也可以看成是『新插入结点的往上上溯两个位置的线段长(高度大小),这里出现了神奇数字2』,之前我说过『AVL的失衡其实是局部小范围的,影响范围不超过四层(或者说不超过三个线段长、不超过三个高度单位大小)』,于是我们作出这样的调整(拎着插入点往上数两个高度单位大小的结点,旋转),2)看图,『13』和『14』重合了,由RR类型的经验,我们知道(而且看这里『13』是单个结点)应该把『13』下移一层作为『14』的孩子
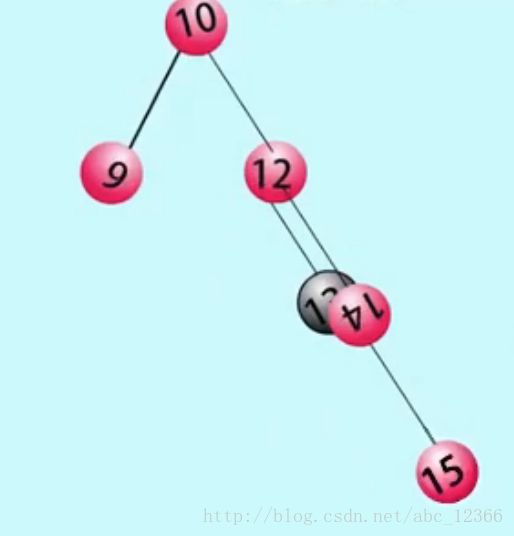
0x03)这就完了,大局已定,剩下的不是写代码的问题(而是画图的问题),我们把结点『12』及其连着的『10』、『9』放下来——大功告成(这也用到了一次旋转,我们说像这样『左右』、『右左』型的都要两次旋转)