平衡二叉搜索树:AVL树的实现与分析 以及 统一重平衡算法 (C++)
平衡二叉搜索树
既然二叉搜索树的性能主要取决于高度,故在节点数目固定的前提下,应尽可能地降低高度。
相应地,应尽可能地使兄弟子树的高度彼此接近,即全树尽可能地平衡。
等价变换
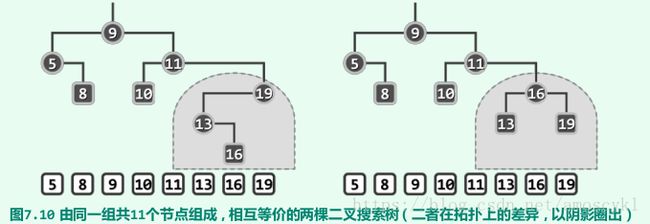
等价二叉搜索树:若两棵二叉搜索树的中序遍历序列相同,则称它们彼此等价;反之亦然。
旋转调整
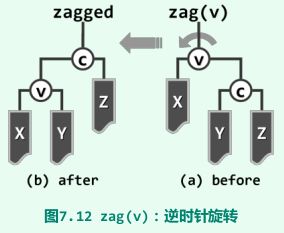
最基本的修复手段,通过围绕特定节点的旋转,实现等价前提下的局部拓扑调整。
zig和zag:
AVL树
平衡因子
任一节点v的平衡因子(balance factor)定义为“其左、右子树的高度差”,即:
balFac(v) = height(lc(v)) - height(rc(v))
所谓AVL树,即平衡因子受限的二叉搜索树其中各节点平衡因子的绝对值均不超过1。
1.接口定义
基于BST模板类,可以直接派生出AVL模板类
#include "../BST/BST.h" //基于BST实现AVL树
template class AVL : public BST { //由BST派生AVL树模板类
public:
BinNodePosi(T) insert(const T& e); //插入(重写)
bool remove(const T& e); //删除(重写)
// BST::search()等其余接口可直接沿用
};
为简化对节点平衡性的判断,算法实现时可借用以下宏定义:
#define Balanced(x) (stature((x).lChild) == stature((x).rChild)) //理想平衡条件
#define BalFac(x) (stature((x).lChild) - stature((x).rChild)) //平衡因子
#define AvlBalanced(x) ((-2 < BalFac(x)) && (BalFac(x) < 2)) //AVL平衡条件
2.节点插入
宏tallerChild()
/******************************************************************************************
* 在左、右孩子中取更高者,若等高,则与父亲p同侧者优先
* 在AVL平衡调整前,借此确定重构方案
******************************************************************************************/
#define tallerChild(x) ( \
stature((x)->lChild) > stature((x)->rChild) ? (x)->lChild : ( \
stature((x)->rChild) > stature((x)->lChild) ? (x)->rChild : ( \
IsLChild(*(x)) ? (x)->lChild : (x)->rChild \
) \
) \
)单旋
如图7.15(a)所示,设v是p的右孩子,且p是g的右孩子。
双旋
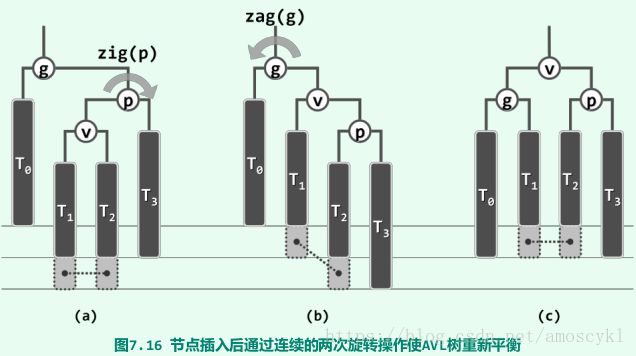
如图7.16(a)所示,设节点v是p的左孩子,而p是g的右孩子。
实现
template BinNodePosi(T) AVL::insert(const T& e) { //将关键码e插入AVL树中
BinNodePosi(T) & x = search(e); if (x) return x; //确认目标节点不存在(留意对_hot的设置)
x = new BinNode(e, _hot); _size++; //创建节点x(此后,其父_hot可能增高,祖父可能失衡)
for (BinNodePosi(T) g = _hot; g; g = g->parent) { //从x之父出发向上,逐层检查各代祖先g
if (!AvlBalanced(*g)) { //一旦发现g失衡,则(采用“3 + 4”算法)使之复衡
FromParentTo(*g) = rotateAt(tallerChild(tallerChild(g))); //将该子树联至原父亲
break; //g复衡后,局部子树高度必然复原;其祖先亦必如此,故调整随即结束
} else //否则(g依然平衡),只需简单地
updateHeight(g); //更新其高度(注意:即便g未失衡,高度亦可能增加)
} //至多只需一次调整;若果真做过调整,则全树高度必然复原
return x; //返回新节点
} //无论e是否存在于原树中,返回时总有x->data == e 3.节点删除
单旋
如图7.17(a)所示,由于在T 3 中删除了节点而致使g(x)不再平衡,但p的平衡因子非负时,
通过以g(x)为轴顺时针旋转一次即可恢复局部的平衡。平衡后的局部子树如图(b)所示。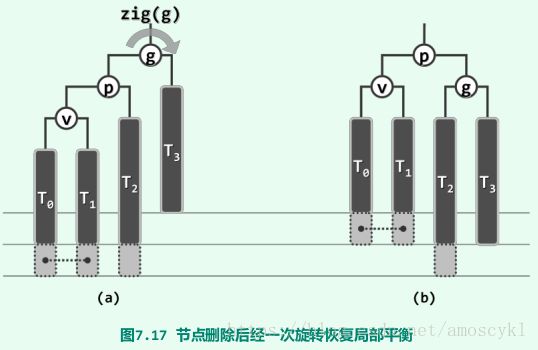
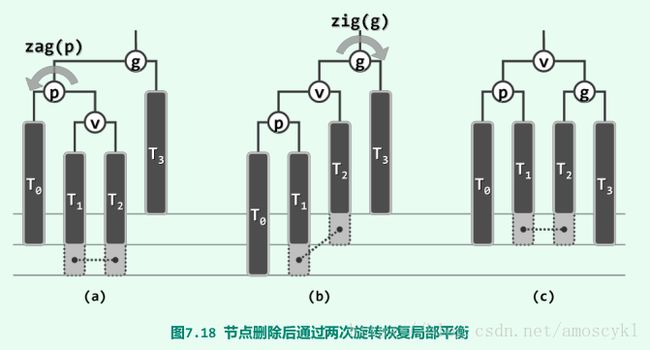
双旋
如图7.18(a)所示,g(x)失衡时若p的平衡因子为-1,则经过以p为轴的一次逆时针旋转之
后(图(b)),即可转化为图7.17(a)的情况。
实现
template bool AVL::remove(const T& e) { //从AVL树中删除关键码e
BinNodePosi(T) & x = search(e); if (!x) return false; //确认目标节点存在(留意对_hot的设置)
removeAt(x, _hot); _size--; //先按BST规则删除之(此后,原节点之父_hot及其祖先均可能失衡)
for (BinNodePosi(T) g = _hot; g; g = g->parent) { //从_hot出发向上,逐层检查各代祖先g
if (!AvlBalanced(*g)) //一旦发现g失衡,则(采用“3 + 4”算法)使之复衡
g = FromParentTo(*g) = rotateAt(tallerChild(tallerChild(g))); //将该子树联至原父亲
updateHeight(g); //并更新其高度(注意:即便g未失衡,高度亦可能降低)
} //可能需做Omega(logn)次调整——无论是否做过调整,全树高度均可能降低
return true; //删除成功
} //若目标节点存在且被删除,返回true;否则返回false
统一重平衡算法
无论对于插入或删除操作,新方法也同样需要从刚发生修改的位置x出发逆行而上,直至遇到最低的失衡节点g(x)。于是在g(x)更高一侧的子树内,其孩子节点p和孙子节点v必然存在,而且这一局部必然可以g(x)、p和v为界,分解为四棵子树。
这就意味着,这一局部应等价于如图7.19所示的子树。更重要的是,纵观图7.15至图7.18可见,这四棵子树的高度相差不超过一层,故只需如图7.19所示将这三个节点与四棵子树重新“组装”起来,恰好即是一棵AVL树!
相应的重构过程,仅涉及局部的三个节点及其四棵子树,故称作“3 + 4”重构。其具体实现如代码7.13所示。
/******************************************************************************************
* 按照“3 + 4”结构联接3个节点及其四棵子树,返回重组之后的局部子树根节点位置(即b)
* 子树根节点与上层节点之间的双向联接,均项由上层调用者完成
* 可用于AVL和RedBlack的局部平衡调整
******************************************************************************************/
template BinNodePosi(T) BST::connect34(
BinNodePosi(T) a, BinNodePosi(T) b, BinNodePosi(T) c,
BinNodePosi(T) T0, BinNodePosi(T) T1, BinNodePosi(T) T2, BinNodePosi(T) T3
) {
a->lChild = T0; if (T0) T0->parent = a;
a->rChild = T1; if (T1) T1->parent = a; updateHeight(a);
c->lChild = T2; if (T2) T2->parent = c;
c->rChild = T3; if (T3) T3->parent = c; updateHeight(c);
b->lChild = a; a->parent = b;
b->rChild = c; c->parent = b; updateHeight(b);
return b; //该子树新的根节点
} 代码7.13 “3 + 4”重构
利用以上connect34()算法,即可视不同情况,按如下具体方法完成重平衡:
/******************************************************************************************
* BST节点旋转发换统一算法(3节点 + 4子树),返回调整之后局部子树根节点的位置
* 注意:尽管子树根会正确指向上层节点(如果存在),但反向的联接须由上局函数完成
******************************************************************************************/
template BinNodePosi(T) BST::rotateAt(BinNodePosi(T) v) { //v为非空的孙辈节点
BinNodePosi(T) p = v->parent; BinNodePosi(T) g = p->parent; //视v、p和g相对位置分四种情况
if (IsLChild(*p)) /* zig */
if (IsLChild(*v)) { /* zig-zig */
p->parent = g->parent; //向上联接
return connect34(v, p, g, v->lChild, v->rChild, p->rChild, g->rChild);
} else { /* zig-zag */
v->parent = g->parent; //向上联接
return connect34(p, v, g, p->lChild, v->lChild, v->rChild, g->rChild);
}
else /* zag */
if (IsRChild(*v)) { /* zag-zag */
p->parent = g->parent; //向上联接
return connect34(g, p, v, g->lChild, p->lChild, v->lChild, v->rChild);
} else { /* zag-zig */
v->parent = g->parent; //向上联接
return connect34(g, v, p, g->lChild, v->lChild, v->rChild, p->rChild);
}
}
完