遗传算法解决TSP问题（C++）

很早做了综合实训，题目是用 遗传算法解决TSP问题。
今天写篇博客，一方面作为分享，另一方面作为知识回顾~

为什么采用遗传算法解决问题呢？因为相比于其他普通算法，遗传算法有很大的优势，它摆脱了传统算法对问题参数的依赖，如连续、可导、可微等限制，只需对参数的编码进行操作，减少了求解问题的复杂性，同时它是一种全局搜索算法避免了陷入局部最优解。
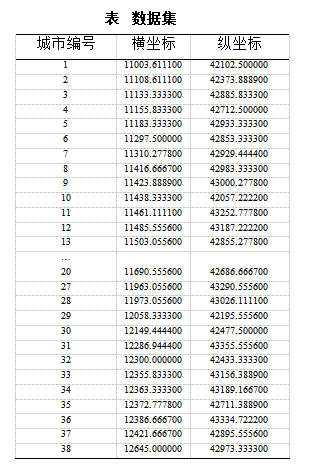
本文章程序中，是求其TSP（38个城市）的近似解；去掉主函数的注释代码，便可以在data.txt文件里读取数据，并在Linux环境下用GNUplot绘制图像。

阅读前先说下本篇文章的思路：首先我们介绍下何为遗传算法及相关概念，之后在粗谈什么是TSP问题，最后在讲解源代码，及程序运行流程和采用的各种策略。

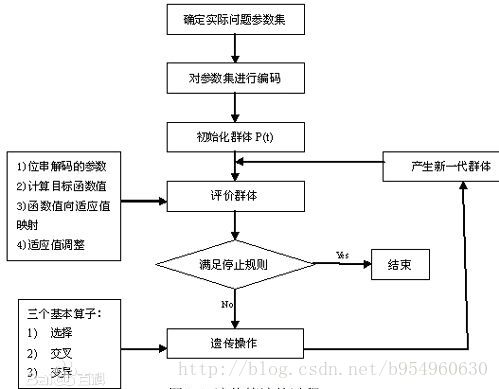
一、基因遗传算法

1.1基因算法简介
遗传算法（Genetic Algorithm）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。遗传算法是从代表问题可能潜在的解集的一个种群（population）开始的，而一个种群则由经过基因（gene）编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码，初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代（generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度（fitness）大小选择（selection）个体，并借助于自然遗传学的遗传算子（genetic operators）进行组合交叉（crossover）和变异（mutation），产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。
1.2基本概念
由于遗传算法是由进化论和遗传学机理而产生的搜索算法，所以在这个算法中会用到很多生物遗传学知识，下面是我们将会用来的一些术语说明：

染色体：
染色体又可以叫做基因型个体(individuals),一定数量的个体组成了群体(population),群体中个体的数量叫做群体大小。
基因：
基因是串中的元素，基因用于表示个体的特征。例如有一个串S=1011，则其中的1，0，1，1这4个元素分别称为基因。它们的值称为等位基因(Alleles)。
基因位点：
基因位点在算法中表示一个基因在串中的位置称为基因位置(Gene Position)，有时也简称基因位。基因位置由串的左向右计算，例如在串 S=1101 中，0的基因位置是3。
特征值：
在用串表示整数时，基因的特征值与二进制数的权一致；例如在串 S=1011 中，基因位置3中的1，它的基因特征值为2；基因位置1中的1，它的基因特征值为8。
适应度：
各个个体对环境的适应程度叫做适应度(fitness)。为了体现染色体的适应能力，引入了对问题中的每一个染色体都能进行度量的函数，叫适应度函数。 这个函数是计算个体在群体中被使用的概率。

1.3遗传算法结构
遗传操作是模拟生物基因遗传的做法。在遗传算法中，通过编码组成初始群体后，遗传操作的任务就是对群体的个体按照它们对环境适应度(适应度评估)施加一定的操作，从而实现优胜劣汰的进化过程。从优化搜索的角度而言，遗传操作可使问题的解，一代又一代地优化，并逼近最优解。
遗传操作包括以下三个基本遗传算子(genetic operator):选择(selection)；交叉(crossover)；变异(mutation)。
这三个遗传算子有如下特点：
个体遗传算子的操作都是在随机扰动情况下进行的。因此，群体中个体向最优解迁移的规则是随机的。需要强调的是，这种随机化操作和传统的随机搜索方法是有区别的。遗传操作进行的高效有向的搜索而不是如一般随机搜索方法所进行的无向搜索。
遗传操作的效果和上述三个遗传算子所取的操作概率，编码方法，群体大小，初始群体以及适应度函数的设定密切相关。

遗传算法的基本运算过程如下：
a)初始化：设置进化代数计数器t=0，设置最大进化代数T，随机生成M个个体作为初始群体P(0)。
b)个体评价：计算群体P(t)中各个个体的适应度。
遗传算法
c)选择运算:将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。
d)交叉运算：将交叉算子作用于群体。遗传算法中起核心作用的就是交叉算子。
e)变异运算：将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。
群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。
f)终止条件判断:若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出，终止计算。

二、TSP问题

旅行商问题，即TSP问题（Travelling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
旅行商问题是一个典型的组合优化问题，并且是一个np难问题，其可能的路径数目与城市数目n是成指数型增长的，所以一般很难精确地求出其最优解，本文采用遗传算法求其TSP（38个城市）的近似解。

三、现在进入正题

1、源代码

#include 
#include 
#include 
#include "math.h"
#include "time.h"
#include 
#include 
#define CITY_NUM 38     //城市数，城市编号是0~CITY_NUM-1
#define POPSIZE 300        //种群个体数
#define MAXVALUE 10000000   //路径最大值上限
#define N 100000//需要根据实际求得的路径值修正
unsigned seed=(unsigned)time(0);
double Hash[CITY_NUM+1];
typedef struct CityPosition
{
    double x;
    double y;
}CityPosition;

CityPosition CityPos[38]={
    {11003.611100,42102.500000},{11108.611100,42373.888900},{11133.333300,42885.833300},{11155.833300,42712.500000},{11183.333300,42933.333300},{11297.500000,42853.333300},{11310.277800,42929.444400},{11416.666700,42983.333300},{11423.888900,43000.277800},{11438.333300,42057.222200},{11461.111100,43252.777800},{11485.555600,43187.222200},{11503.055600,42855.277800},{11511.388900,42106.388900},{11522.222200,42841.944400},{11569.444400,43136.666700},{11583.333300,43150.000000},{11595.000000,43148.055600},{11600.000000,43150.000000},{11690.555600,42686.666700},{11715.833300,41836.111100},{11751.111100,42814.444400},{11770.277800,42651.944400},{11785.277800,42884.444400},{11822.777800,42673.611100},{11846.944400,42660.555600},{11963.055600,43290.555600},{11973.055600,43026.111100},{12058.333300,42195.555600},{12149.444400,42477.500000},{12286.944400,43355.555600},{12300.000000,42433.333300},{12355.833300,43156.388900},{12363.333300,43189.166700},{12372.777800,42711.388900},{12386.666700,43334.722200},{12421.666700,42895.555600},{12645.000000,42973.333300}
};

double CityDistance[CITY_NUM][CITY_NUM];//城市距离词典

typedef struct{
    int colony[POPSIZE][CITY_NUM+1];//城市种群,默认出发城市编号为0，则城市编号的最后一个城市还应该为0
    double fitness[POPSIZE];// 每个个体的适应值，即1/Distance[POPSIZE]
    double Distance[POPSIZE];//每个个体的总路径
    int BestRooting[CITY_NUM+1];//最优城市路径序列
    double BestFitness;//最优路径适应值
    double BestValue;//最优路径长度
    int BestNum;
}TSP,*PTSP;

/*计算城市距离词典CityDistance[i][j]*/
void CalculatDist()
{
    int i,j;
    double temp1,temp2;
    for(i=0;ifor(j=0;j<=CITY_NUM;j++){//最后一个城市还应该返回到出发节点
            temp1=CityPos[j].x-CityPos[i].x;
            temp2=CityPos[j].y-CityPos[i].y;
            CityDistance[i][j]=sqrt(temp1*temp1+temp2*temp2);
        }
    }
}
/*数组复制*/
void copy(int a[],int b[])
{
    int i=0;
    for(i=0;i1;i++)
    {
        a[i]=b[i];
    }
}

/*用来检查新生成的节点是否在当前群体中，0号节点是默认出发节点和终止节点*/
bool check(TSP &city,int pop,int num,int k)
{
    int i;
    for(i=0;i<=num;i++){
        if(k==city.colony[pop][i])
            return true;//新生成节点存在于已经生成的路径中
    }
    return false;//新生成节点没有存在于已经生成的路径中
}

/****************种群初始化，即为city.colony[i][j]赋值****************/
void InitColony(TSP &city)
{
    int i,j,r;
    for(i=0;i0]=0;
        city.colony[i][CITY_NUM]=0;
        city.BestValue=MAXVALUE;
        city.BestFitness=0;//适应值越大越好
    }

    for(i=0;ifor(j=1;j1)+1;//产生1～CITY_NUM-1之间的随机数
            while(check(city,i,j,r))//随机产生城市序号，即为city.colony[i][j]赋值
            {
                r=rand()%(CITY_NUM-1)+1;
            }

            city.colony[i][j]=r;
        }
    }
}

/*计算适应值,考虑应该在这里面把最优选出来*/
void CalFitness(TSP &city)
{
    int i,j;
    int start,end;
    int Best=0;
    for(i=0;i//求每个个体的总路径，适应值
        city.Distance[i]=0;
        for(j=1;j<=CITY_NUM;j++){
            start=city.colony[i][j-1];end=city.colony[i][j];
            city.Distance[i]=city.Distance[i]+CityDistance[start][end];//city.Distance[i]每个个体的总路径
        }
        city.fitness[i]=N/city.Distance[i];
        if(city.fitness[i]>city.fitness[Best])//选出最大的适应值，即选出所有个体中的最短路径
            Best=i;
    }
    copy(city.BestRooting,city.colony[Best]);//将最优个体拷贝给city.BestRooting
    city.BestFitness=city.fitness[Best];
    city.BestValue=city.Distance[Best];
    city.BestNum=Best;
}


/****************选择算子：轮盘赌法****************/
void Select(TSP &city)
{
    int TempColony[POPSIZE][CITY_NUM+1];
    int i,j,t;
    double s;
    double GaiLv[POPSIZE];
    double SelectP[POPSIZE+1];
    double avg;
    double sum=0;
    for(i=0;ifor(i=0;i0]=0;
    for(i=0;i1]=SelectP[i]+GaiLv[i]*RAND_MAX;
    }
    memcpy(TempColony[0],city.colony[city.BestNum],sizeof(TempColony[0]));//void *memcpy(void *dest, const void *src, size_t n)从源src所指的内存地址的起始位置开始拷贝n个字节到目标dest所指的内存地址的起始位置中
    for(t=1;tdouble ran = rand() % RAND_MAX + 1;
        s= (double) ran / 100.0;
        for(i=1;iif(SelectP[i]>=s)
                break;
        }
        memcpy(TempColony[t],city.colony[i-1],sizeof(TempColony[t]));
    }
    for(i=0;i/****************交叉：头尾不变，中间打乱顺序交叉****************/
void Cross(TSP &city,double pc)//交叉概率是pc
{
    int i,j,t,l;
    int a,b,ca,cb;
    int Temp1[CITY_NUM+1],Temp2[CITY_NUM+1];
    for(i=0;idouble s=((double)(rand()%RAND_MAX))/RAND_MAX;
        if(sif(ca==city.BestNum||cb==city.BestNum)//如果遇到最优则直接进行下次循环
                continue;

            l=rand()%19+1;  //1-19
            a=rand()%(CITY_NUM-l)+1; //1-37

            memset(Hash,0,sizeof(Hash));//void *memset(void *s, int ch, size_t n);将s中当前位置后面的n个字节 用 ch 替换并返回 s 。
            Temp1[0]=Temp1[CITY_NUM]=0;
            for(j=1;j<=l;j++)//打乱顺序即随机，选出来的通过Hash标记为1
            {
                Temp1[j]=city.colony[cb][a+j-1]; //a+L=2~38 20~38
                Hash[Temp1[j]]=1;
            }
            for(t=1;tif(Hash[city.colony[ca][t]]==0)
                {
                    Temp1[j++]=city.colony[ca][t];
                    Hash[city.colony[ca][t]]=1;
                }
            }
            memcpy(city.colony[ca],Temp1,sizeof(Temp1));
        }
    }

}

/****************变异****************/
double GetFittness(int a[CITY_NUM+1])
{
    int i,start,end;
    double Distance=0;
    for(i=0;i1];
        Distance+=CityDistance[start][end];
    }
    return N/Distance;
}
/*对换变异*/
void Mutation(TSP &city,double pm)//变异概率是pm
{
    int i,k,m;
    int Temp[CITY_NUM+1];
    for(k=0;kdouble s=((double)(rand()%RAND_MAX))/RAND_MAX;//随机产生概率0~1间
        i=rand()%POPSIZE;//随机产生0~POPSIZE之间的数
        if(s//i!=city.BestNum，即保证最优的个体不变异
        {
            int a,b,t;
            a=(rand()%(CITY_NUM-1))+1;
            b=(rand()%(CITY_NUM-1))+1;
            copy(Temp,city.colony[i]);
            if(a>b)//保证让b>=a
            {
                t=a;
                a=b;
                b=t;
            }
            for(m=a;m<(a+b)/2;m++)
            {
                t=Temp[m];
                Temp[m]=Temp[a+b-m];
                Temp[a+b-m]=t;
            }

            if(GetFittness(Temp)1))+1;
                b=(rand()%(CITY_NUM-1))+1;
                //copy(Temp,city.colony[i]);
                memcpy(Temp,city.colony[i],sizeof(Temp));
                if(a>b)
                {
                    t=a;
                    a=b;
                    b=t;
                }
                for(m=a;m<(a+b)/2;m++)
                {
                    t=Temp[m];
                    Temp[m]=Temp[a+b-m];
                    Temp[a+b-m]=t;
                }

                    if(GetFittness(Temp)1))+1;
                        b=(rand()%(CITY_NUM-1))+1;
                        //copy(Temp,city.colony[i]);
                        memcpy(Temp,city.colony[i],sizeof(Temp));
                        if(a>b)
                        {
                            t=a;
                            a=b;
                            b=t;
                        }
                        for(m=a;m<(a+b)/2;m++)
                        {
                            t=Temp[m];
                            Temp[m]=Temp[a+b-m];
                            Temp[a+b-m]=t;
                        }
                    }

            }
            memcpy(city.colony[i],Temp,sizeof(Temp));
        }
    }
}

void OutPut(TSP &city)
{
    int i,j;
    printf("最佳路径为:\n");
    for(i=0;i<=CITY_NUM;i++)
    printf("%5d",city.BestRooting[i]);
    printf("\n最佳路径值为：%f\n",(city.BestValue));
}


int main()
{
        TSP city;
        double pcross,pmutation;//交叉概率和变异概率
        int MaxEpoc;//最大迭代次数
        int i;
        srand(seed);
        MaxEpoc=30000;
        pcross=0.5; pmutation=0.05;
        CalculatDist();//计算城市距离词典
        InitColony(city);//生成初始种群
        CalFitness(city);//计算适应值,考虑应该在这里面把最优选出来

        for(i=0;i//选择(复制)：轮盘赌法
            Cross(city,pcross);//交叉
            Mutation(city,pmutation);//变异
            CalFitness(city);//计算适应值
        }

       OutPut(city);//输出

/*******注释代码是从data.txt文件里读取数据*******/
/*******并在Linux中用GNUplot绘制图像*******/
    /*freopen("data.txt", "w",stdout);
    for(i = 0; i < POPSIZE-1; i ++)
    {
        printf("%d %.5lf\n", i,city.Distance[i]);
        printf("%d %.5lf\n", i+1,city.Distance[i+1]);
    }
    printf("\n");
   for(i = 0; i < POPSIZE-1; i ++)//平均值：每一代的路径和除以总个数
    {
        printf("%d %.5lf\n", i,avedistance[i]);
        printf("%d %.5lf\n", i+1,avedistance[i+1]);
    }
    FILE *fpp=popen("gnuplot","w");
    char *aa="plot for [i=0:399] \"data.txt\" index i with lines\n";
    fprintf(fpp,"%s",aa);
    fflush(fpp);
    sleep(100);*/
    return 0;
}

想见data.txt文件里内容，请下载本人上传的资源《遗传算法解决TSP问题（全）》

2、上面程序的运行流程

（1）初始化各种变量：
种群个体数：300，城市数：38，迭代次数：4000，各城市坐标，交叉概率，变异概率等等。
计算距离词典CityDistance[i][j]：即每个城市距其他城市的实际距离。
注：本文采用TSP问题公测数据集网站（http://www.tsp.gatech.edu/index.html ） 上的公测数据。测试的城市的数量为38个。

（2）种群初始化：
种群初始化即初始化city.colony[i][j]，city.colony[i][j]中的i代表种群的个体数，这里为300，j代表每个个体的基因（即城市的序列）。每个个体都拥有一个染色体，每个染色体都拥有38个基因，每个基因代表一座城市，每个基因的值即城市的序列，我们随机产生38个不同的城市序列（0~37），至于编码方式，本次我们采用的实数编码。

（3）适应度函数：
适应度函数通常取路径长度T的倒数,即f=1/T
而我们的适应度函数为某个修正值N除以路径长度T，即 f=N/T, 这里我们之所以加入修正值，是因为通过适当的N值能让结果更趋于稳定和精准，但N稳定精准的能力有限，且当N大于某个值时效果不再明显。
我们通过一开始求出的距离词典得出每个个体的总路径长度，从而求得适应度函数。适应度越大，路径越短。我们再通过比较适应度得出最适适应值city.Distance[Best]，并得到最优个体city.colony[Best]。

（4）选择过程：
用随机方法产生初始种群。适应度比例选择，（精英保留）产生新一代种群。
选择机制与群体构成：在新一代群体构成方法方面，采用了 保留一个最好的父串的最佳保留（eliti）群体构造方式。
其中采用了轮盘赌法，所占比率 = 个体适应度 / 总适应度，每次旋转都为新的种群选择一个染色体。

（5）交叉过程：
交叉概率Pc为0.5，首先保留精英个体，之后其他个体采用了算术重组，每个父代的第一个和最后一个基因不变，中间基因随机打乱顺序重组交叉（头尾不变，中间变）。

（6）变异过程：
变异概率是pm为0.05，首先保留精英个体保证最优个体不变异，之后采用了 对换变异 的策略，通过随机选择串中的两个位点进行变异，之后再对变异后的个体进行两次适应度评估，若小于变异前的适应度则再变异。

（7）循环操作：
判断是否满足设定的迭代数MaxEpoc，否，则继续迭代；是，则结束遗传操作，跳出。

3、上面所用的策略及实现

（1）编码方式：一般编码方法有 二进制编码法、格雷码编码法、浮点编码法、符号编码法，而本次直接采用的实数编码。
（2）群体构成：精英保留
在新一代群体构成方法方面存在四种方式：
N方式：全部替换上一代群体的全刷新代际更新方式。
E方式：保留一个最好的父串的最佳保留（elitist）群体构造方式。
G方式：按一定比例更新群体中的部分个体的部分更新方式（或称代沟方法，这种情况的极端是每代仅删去一个最不适的个体的最劣死亡方式）。
B方式：从产生的子代和父代中挑选最好的若干个个体的群体构成形式。
一般讲，N方式的全局搜索性能最好，但收敛速度最慢；B方式收敛速度最快，但全局搜索性能最差；E方式和G方式的性能介于N方式和B方式之间。在求解货郎担问题的应用中，多选用E方式。
出于性能考虑，本次综合实训中采用了E方式，在初代的选择，每一代的选择交叉、变异都使用了精英保留的思想。

（3）选择算子：轮盘赌法
为了使高适应度个体的基因具有更高的概率遗传给下一代，我们采用了赌盘选择算子作为本实验的选择函数。
轮盘赌法，又称比例选择方法．其基本思想是：各个个体被选中的概率与其适应度大小成正比．

具体操作如下：
a)计算出群体中每个个体的适应度f(i=1，2，…，M)，M为群体大小；
b)计算出每个个体被遗传到下一代群体中的概率；

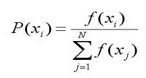
c)计算出每个个体的累积概率；
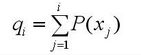（q[i]称为染色体x[i] (i=1, 2, …, n)的积累概率）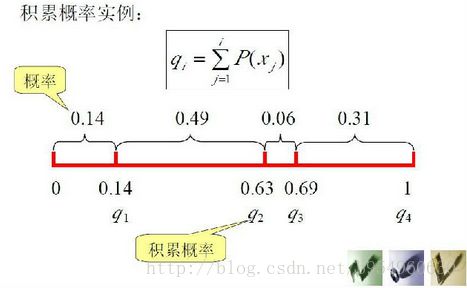
d)在[0，1]区间内产生一个均匀分布的伪随机数r；
e)若r < q[1]，则选择个体1，否则，选择个体k，使得：q[k-1]< r ≤q[k] 成立；
f)重复d)、e)共M次

（4）交叉算子：算术重组
有性繁殖是自然生物进化的普遍现象，同源染色体通过交叉实现基因重组，从而生成新的个体。交叉操作通过组合不同个体的遗传信息（基因）以生成可能的优良个体，是遗传算法生成新个体的主要方法。交叉算子一般为一点交叉、多点交叉和均匀交叉，离散重组和算术重组等。我们采用的是算术重组。
算术重组：在实数编码下，算术重组指子代个体的基因（目标变量的分量）由父代个体的相应位置上的基因的线性组合而成。

（5）变异算子：对换变异
遗传算法引入变异的目的有两个:一是使遗传算法具有局部的随机搜索能力。当遗传算法通过交叉算子已接近最优解邻域时，利用变异算子的这种局部随机搜索能力可以加速向最优解收敛。显然，此种情况下的变异概率应取较小值，否则接近最优解的积木块会因变异而遭到破坏。二是使遗传算法可维持群体多样性，以防止出现未成熟收敛现象。此时收敛概率应取较大值。针对TSP问题，主要的变异技术有位点变异、逆转变异、对换变异、插入变异，这里我们采用的是对换变异。

对换变异：
随机选择串中的两点，交换其值（码）。对于串A
A＝1 2 3 4 5 6 7 8 9
若对换点为4，7，则经对换后，A’为
A’＝1 2 3 7 5 6 4 8 9

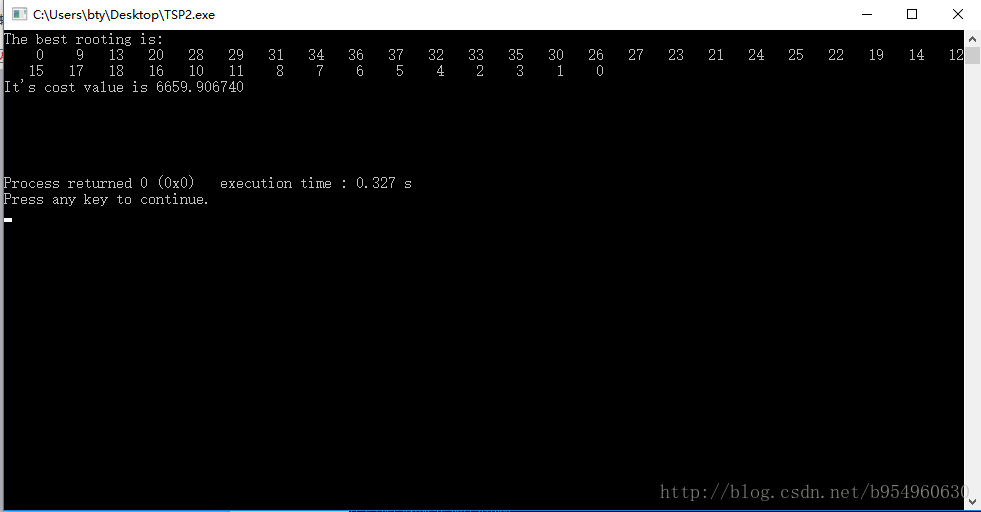
4、代码的运行结果

TSP数据集网站(http://www.tsp.gatech.edu/world/djtour.html) 上公测的最优结果6656。

下面是试验运行结果：为6659.906740，比最短路径大3.91

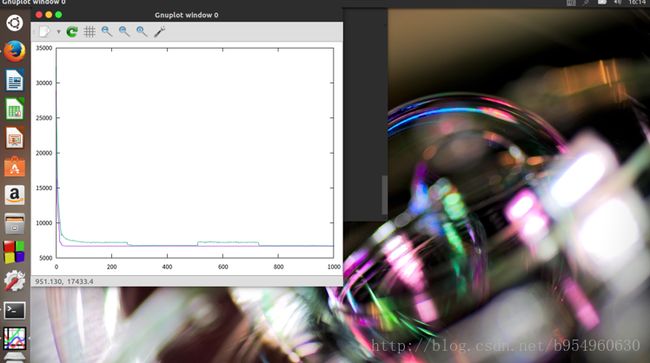
去掉main()函数的注释后，下图为GNUplot绘制的平均值，最适値图像图像

5、设想

我们如何让更多的精英个体存活下来，还能维持保证物种的丰富度，从而减少更多的算法运行时间?
我们先把群体分成不同的两组，即在两个环境不同的地域生存，形成地理隔离，这样做得目的是增加种群的丰富度。之后我们把两个不同群体的生存环境变为恶略（即两种不同的更苛刻复杂的选择标准），这样做得目的是让更多的精英个体存活下来。当两个种群繁殖到一定标准后，再将他们合并为一个种群，最终通过某种标准更快的产生全局最优解。