计算机视觉中的多视图几何——第一章:2D摄影几何(4.从图形中恢复仿射和度量性质)
计算机视觉中的多视图几何——第一章:2D摄影几何(4.从图像中恢复仿射和度量性质
- 一、仿射恢复
- 1.1 无穷远线
- 1.2 由图像恢复仿射性质
- 二、虚圆点及其对偶
- 2.1 虚圆点
- 2.2 与虚圆点对偶的二次曲线
- 2.3 射影平面的夹角
- 三、由图像恢复度量性质
射影矫正主要是为了消除平面的透视图中的射影失真,使得原始平面的相似性质能够被测量。在射影变换后的平面中, 当无穷远线 I ∞ \bm{I}_\infty I∞的像被确定之后,射影失真可消除,而虚圆点被确认之后,仿射失真可消除,仅剩相似失真。
一、仿射恢复
1.1 无穷远线
在射影变换下理想点可映射为有限点,无穷远线 I ∞ \bm{I}_\infty I∞可映射为有限直线。而在仿射变换下, I ∞ \bm{I}_\infty I∞依然映射为无穷远线。推导如下:
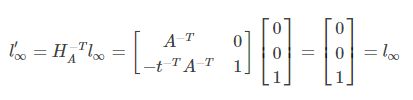
结论1 : 在射影变换 H H H下,无穷远直线 I ∞ \bm{I}_\infty I∞为不动直线的充要条件是 H H H是仿射变换。
仿射变换下, I ∞ \bm{I}_\infty I∞不是点点不动的,仿射变换 I ∞ \bm{I}_\infty I∞被映射为 I ∞ \bm{I}_\infty I∞的点,当它不是原来的点。只是无穷远线集合不动,而非点点不动。
1.2 由图像恢复仿射性质
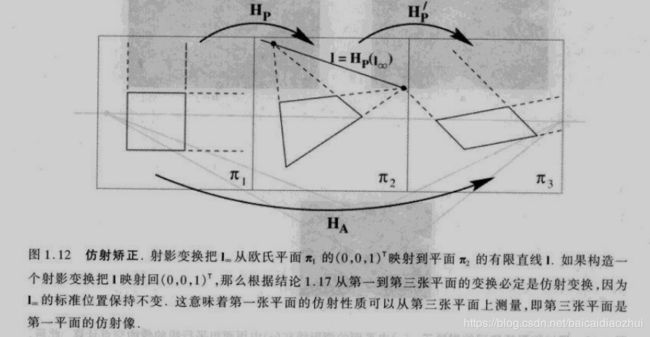
根据结论1中无穷远线在仿射变换下为不动直线的性质。如果能够在射影变换所得的平面内找到无穷远直线的象(一般为有限直线),并通过重映射将该有限直线像重新变换为无穷远线,并将这种重映射推广至于整个平面,即可消除射影失真,恢复平面的仿射性质。
如图所示,原始平面 π 1 \pi_1 π1射影变换所得平面为 π 2 \pi_2 π2,如果能够在该 π 2 \pi_2 π2平面能找到无穷远直线 I ∞ \bm{I}_\infty I∞=(0,0,1)^T的象,即有限直线 I \bm{I} I。且有限直线 I \bm{I} I通过矩阵 H H H的变换,能够重新转换为无穷远直线 I ∞ \bm{I}_\infty I∞,那么利用矩阵 H H H作用与整个 π 2 \pi_2 π2平面,可以得到平面 π 3 \pi_3 π3,所得平面与原始平面 π 1 \pi_1 π1之间射影失真被消除,只存在仿射变换的关系。
当无穷远直线的象 I = ( l 1 , l 2 , l 3 ) T \bm{I}=(l_1,l_2,l_3)^T I=(l1,l2,l3)T,假定 l 3 ̸ = 0 l_3\not=0 l3̸=0,那么 I \bm{I} I映射为 I ∞ = ( 0 , 0 , 1 ) T \bm{I_\infty}=(0,0,1)T I∞=(0,0,1)T的一个适合的变换为:
H = H A [ 1 0 0 0 1 0 l 1 l 2 l 3 ] H=H_A \begin{bmatrix} 1&0&0\\ 0&1&0\\ l_1&l_2&l_3 \end{bmatrix} H=HA⎣⎡10l101l200l3⎦⎤
有: H − T ( l 1 , l 2 , l 3 ) T = ( 0 , 0 , 1 ) T = I ∞ H^{-T}(l_1,l_2,l_3)^T=(0,0,1)^T=\bm{I_\infty} H−T(l1,l2,l3)T=(0,0,1)T=I∞
注:射影变换可将理想点转换成平面内的有限点,将无穷远直线转换为有限直线;
-
消影点和消影线 :
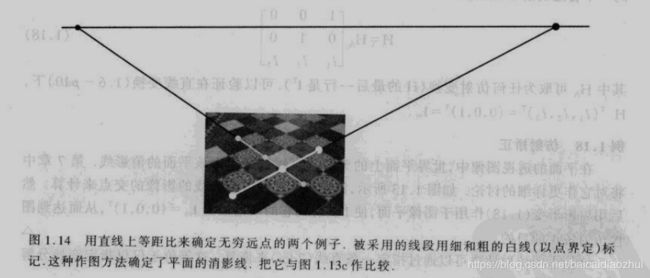
在平面的透视图像中,世界平面的无穷远直线被影像为该平面的消影线。消影点为世界平面上两平行直线相交的理想点在透视图像中的像,因此消影点位于消影线上。确定两个不同的消影点,即可确认出消影线。 -
消影点计算(代数法):
给定直线上有两个已知长度比的线段,该直线上的无穷远点便可以确认。
例如:当给定直线上的三点在世界坐标系下坐标为 x ˉ 1 , x ˉ 2 , x ˉ 3 \bm{\bar{x}_1},\bm{\bar{x}_2},\bm{\bar{x}_3} xˉ1,xˉ2,xˉ3,射影变换后坐标为: x ˉ 1 ′ , x ˉ 2 ′ , x ˉ 3 ′ \bm{\bar{x}'_1},\bm{\bar{x}'_2},\bm{\bar{x}'_3} xˉ1′,xˉ2′,xˉ3′,由于射影变换中任何共线四点的交比不变,在已知三点的情况下,将选取理想点作为世界坐标下的第四点 x ˉ 4 = ( 1 , 0 ) T \bm{\bar{x}_4}=(1,0)^T xˉ4=(1,0)T,取消影点作为射影变换图像下的第四点 x ˉ 4 ′ \bm{\bar{x}_4'} xˉ4′,根据交比不变可以计算消影点 x ˉ 4 ′ \bm{\bar{x}_4'} xˉ4′的坐标;
C r o s s ( x ˉ 1 ′ , x ˉ 2 ′ , x ˉ 3 ′ , x ˉ 4 ′ ) = C r o s s ( x ˉ 1 , x ˉ 2 , x ˉ 3 , x ˉ 4 ) Cross(\bm{\bar{x}'_1},\bm{\bar{x}'_2},\bm{\bar{x}'_3},\bm{\bar{x}'_4})=Cross(\bm{\bar{x}_1},\bm{\bar{x}_2},\bm{\bar{x}_3},\bm{\bar{x}_4}) Cross(xˉ1′,xˉ2′,xˉ3′,xˉ4′)=Cross(xˉ1,xˉ2,xˉ3,xˉ4)
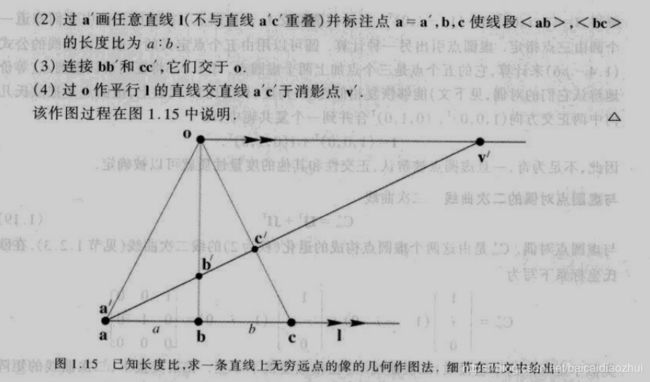
- 消影点计算(几何法):
二、虚圆点及其对偶
2.1 虚圆点
在相似变换下, I ∞ \bm{I_{\infty}} I∞上有两个不动点,他们是虚圆点(也称绝对点) I , J \bm{I,J} I,J,其标准坐标为:
I = [ 1 i 0 ] ; J = [ 1 − i 0 ] \bm{I}=\begin{bmatrix}1\\i\\0\end{bmatrix} ; \bm{J}=\begin{bmatrix}1\\-i\\0\end{bmatrix} I=⎣⎡1i0⎦⎤;J=⎣⎡1−i0⎦⎤
结论2: 在射影变换 H H H下,虚圆点 I \bm{I} I和 J \bm{J} J为不动点的充要条件是 H H H为相似变换
任何圆都交 I ∞ \bm{I_\infty} I∞于虚圆点;当二次曲线为圆时,有a=c=1,且b=0,则:
x 1 2 + x 2 2 + d x 1 x 2 + e x 2 x 3 + f x 3 2 = 0 x_1^2+x_2^2+dx_1x_2+ex_2x_3+fx_3^2=0 x12+x22+dx1x2+ex2x3+fx32=0
二次曲线与理想直线 I ∞ \bm{I_\infty} I∞相交时 x 3 = 0 x_3=0 x3=0;即有:
x 1 2 + x 2 2 = 0 x_1^2+x_2^2=0 x12+x22=0
求解,可得 I = ( 1 , i , 0 ) T , J = ( 1 , − i , 0 ) T \bm{I}=(1,i,0)^T,\bm{J}=(1,-i,0)^T I=(1,i,0)T,J=(1,−i,0)T,即任何圆都交 I ∞ \bm{I_\infty} I∞于虚圆点。由于二次曲线是需要5个点才能确认,而圆作为二次曲线的一种,只需要3个点就可以进行确认,而加上两个虚圆点后,同样是5个点。
2.2 与虚圆点对偶的二次曲线
二次曲线: C ∞ ∗ = I J T + J I T C^*_\infty=\bm{IJ}^T+\bm{JI}^T C∞∗=IJT+JIT
C ∞ ∗ = [ 1 i 0 ] ( 1 , − i , 0 ) + [ 1 − i 0 ] ( 1 , i , 0 ) = [ 1 0 0 0 1 0 0 0 0 ] C^*_\infty=\begin{bmatrix}1\\i\\0\end{bmatrix} (1,-i,0)+\begin{bmatrix}1\\-i\\0\end{bmatrix}(1,i,0) =\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix} C∞∗=⎣⎡1i0⎦⎤(1,−i,0)+⎣⎡1−i0⎦⎤(1,i,0)=⎣⎡100010000⎦⎤
由于虚圆点在相似变换下的不动性质,二次曲线 C ∞ ∗ C^*_\infty C∞∗在相似变换下也不变:
C ∞ ∗ ′ = H s C ∞ ∗ H s T = C ∞ ∗ {C^*_\infty}'=H_s{C^*_\infty}H_s^T={C^*_\infty} C∞∗′=HsC∞∗HsT=C∞∗
结论3:对偶二次曲线 C ∞ ∗ C^*_\infty C∞∗,在射影变换H下不变的充要条件是H是相似变换。
性质1: C ∞ ∗ C^*_\infty C∞∗有四个自由度;
性质2: I ∞ 是 C ∞ ∗ \bm{I_\infty}是C^*_\infty I∞是C∞∗*的零矢量;
2.3 射影平面的夹角
欧式几何中两直线的夹角有他们的法线点乘计算,直线 I = ( l 1 , l 2 , l 3 ) T \bm{I}=(l_1,l_2,l_3)^T I=(l1,l2,l3)T和 m = ( m 1 , m 2 , m 3 ) T \bm{m}=(m_1,m_2,m_3)^T m=(m1,m2,m3)T之间的夹角为:
cos θ = l 1 m 1 + l 2 m 2 ( l 1 2 + l 2 2 ) ( m 1 2 + m 2 2 ) \cos\theta=\frac {l_1m_1+l_2m_2} {\sqrt{\smash[b]{(l_1^2+l_2^2)(m_1^2+m_2^2)}}} cosθ=(l12+l22)(m12+m22)l1m1+l2m2
射影变换后,夹角计算公式为:
cos θ = I T C ∞ ∗ m ( I T C ∞ ∗ I ) ( m T C ∞ ∗ m ) \cos\theta=\cfrac { \bm{I}^TC_\infty^*\bm{m}} {\sqrt{\smash[]{ (\bm{I}^TC_\infty^*\bm{I}) (\bm{m}^TC_\infty^*\bm{m}) }}} cosθ=(ITC∞∗I)(mTC∞∗m)ITC∞∗m
结论4:一旦二次曲线 C ∞ ∗ C_\infty^* C∞∗在射影平面上能够被辨认,那么欧式叫可以用上式来测量;
结论5:如果 I T C ∞ ∗ m = 0 \bm{I}^TC_\infty^*\bm{m}=0 ITC∞∗m=0则直线 I \bm{I} I和 m \bm{m} m正交;
**长度比:**一旦 C ∞ ∗ C_\infty^* C∞∗被辨认,长度比同样可以测量;
三、由图像恢复度量性质
对偶二次曲线 C ∞ ∗ C_\infty^* C∞∗几乎包含了实现度量矫正所需的全部信息。它能确定射影变换中的仿射和射影成分,而只留下相似变换的失真。
结论6:在射影平面上,一旦 C ∞ ∗ C_\infty^* C∞∗辨认, 那么射影失真可以矫正到相差一个相似变换。