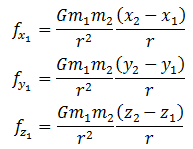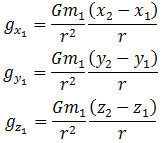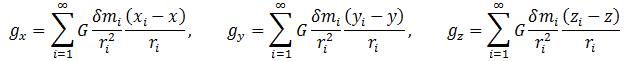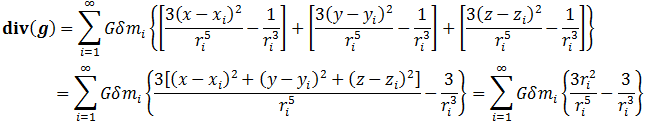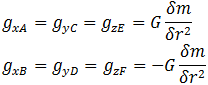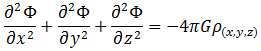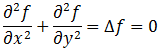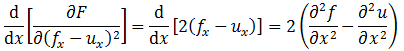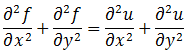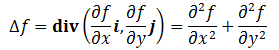从泊松方程到泊松融合（Poisson Matting）

引言

数学无疑是现代数字图像处理技术的一个重要基石，一些效果显著的同时也非常popular的图像处理技术中大量地借鉴和利用了经典数学理论中的一些著名的成果。尽管这些经典数学理论在其原有场景中的意义与其在图像处理技术中的应用二者之间的关系并没有那么obvious！泊松方程（Poisson Equation）在泊松图像编辑（Poisson Image Editing）以及泊松融合（Poisson Matting）中的应用就是一个典型的例子。

西莫恩·德尼·泊松（Siméon-Denis Poisson）是十九世纪法国著名数学家，曾经师从拉普拉斯和拉格朗日两位大师学习数学，数学中许多重要的概念（例如泊松分布、泊松积分、泊松方程 … …） 都以他的名字命名。 

自然科学与工程技术中种种运动发展过程与平衡现象各自遵守一定的规律。这些规律的定量表述一般地呈现为关于含有未知函数及其导数的方程。我们将只含有未知多元函数及其偏导数的方程，称之为偏微分方程（PDE）。椭圆方程是工程技术应用中所涉及的偏微分方程里最为普遍的一种形式。根据椭圆方程的具体形式又可以将其分为以下三种形式，即拉普拉斯方程、泊松方程和亥姆霍兹方程。更多偏微分方程的知识，你可以参考由厦门大学谭忠教授主讲的中国大学MOOC公开课^[1]。这里，我们重点关注的是泊松方程（二维情况下）：

因为关于泊松方程之于图像处理的应用，已经有多篇重要论文发表于国际定义学术会议之上，例如文献[2]、[3]和[4]。但是由于很多图像方面的初学者对于偏微分方程比较陌生，导致在面对泊松融合或泊松图像编辑方面的话题时仍然感觉难度较大。

事实上，所有的偏微分方程都不是无中生有的，而是从现实物理现象中抽象出来的数学表达。要深刻理解图像处理中泊松方程的应用，一方面我们应该从经典物理问题中导出泊松方程为什么是上面给出的那种形式（或者说它的物理意义到底是什么），另外一方面我们还要建立一种从经典物理（或者纯数学的）泊松方程到其之于图像处理中应用的桥梁。微软亚洲研究院前院长沈向洋博士（他同时也是ACM fellow 和IEEE fellow）的一份讲稿[5]很好地解决了上述两个问题。本文相当于是对上述文献的一种解读，如果你感觉自己可以非常轻松地读懂沈博士的演示文稿，大可不必费时间在本文上。

泊松方程的推导

经典物理中，引力场和电场都可以导出泊松方程（沈博士的PPT中都有提及），我们将从前者（即引力场）角度来推导泊松方程。牛顿的万有引力定律指出，任意两个质点有通过连心线方向上的力相互吸引。该引力大小与它们质量的乘积成正比与它们距离的平方成反比，即

其中，G=6.67×10^-11 N⋅m²⋅kg^-2是万有引力常数，m₁和m₂分别是两个物体的质量，r是两个物体之间的距离。

在三维空间中，可以用向量将上述万有引力定律改写为如下形式

这里的f_x1，f_y1和f_z1分别是作用于物体m₁上的引力向量f₁在x、y和z三个方向上的分量。两个物体在空间中的坐标分别为(x₁,y₁,z₁)和(x₂,y₂,z₂)。
根据牛顿第二运动定律，F=ma，可知物体m₁感受到的重力加速度向量g₁在x、y和z三个方向上的分量g_x1，g_y1和g_z1分别为

单位质量的重力势能Φ，单位是焦耳/千克，代表一个给定部位每个单位质量的势能的总和，与局部质量和周围质量的相互作用有关。对于Φ的另一个解释是用来将一个单位的质量从一个地点移至无穷远（与其他质量无相互作用）所需要的工作量的总和。因为这个工作量总是为正数，所以势能总和与重力势能在无穷远处为最大。相对重力势能（相比无穷远处的势能变化）则总是为负数。

单位质量的重力势能在空间坐标系的局部导数等同于相应的重力加速度向量的分量，即

上式中等号右边的负号反映了重力势能的增加与局部重力引力的方向相反，即只有与局部重力势能相反方向的力才能增加重力势能。
做功是指能量由一种形式转化为另一种的形式的过程。当一个外力作用在物体上时，功的大小就定义为作用在物体位移方向上的力与物体位移的乘积。进而有

其中dΦ_x，dΦ_y和dΦ_z是每个单位质量中由于相应坐标的微小变化(dx,dy,dz)引起的重力势能的增加。

根据牛顿万有引力定律，一个连续介质中某个给定点的由于周围物体的引力而感受到的重力加速度g=(g_x, g_y, g_z )是由每个小物体δm_i导致的加速度累加而成的（积分），即

其中，

x_i、y_i和z_i分别是第i个物质元素的坐标，而r_i是这个元素和给定点之间的距离。

根据拉普拉斯算子的定义，可得

再根据前面已经得到的公式，可以得出

而根据散度公式，同样可以得到加速度场的散度表达式为

即

将g_x、g_y和g_z的表达式的表达式带入，可得

注意r_i也是关于x、y和z的函数，于是根据两个函数商的求导法则，以及复合函数求导法则可得

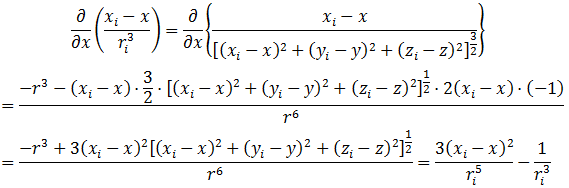
于是有

注意这里的微分是针对给定点的坐标x、y和z完成的，而不是取决于那些于x、y和z无关的周围的质量(x_i, y_i, z_i)。对于所有r_i≠0的情况，上述方程的值显然为0。这意味着一个给定点的重力加速度的散度与周围质量无关，并且必须来自于它自身。
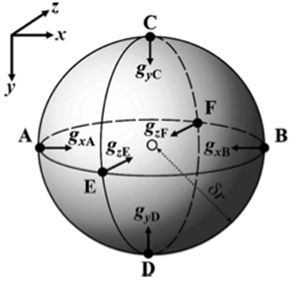
现在将积分的体积缩小至质量为δm，半径为δr的小球体，如下图所示。这个小球体的加速度的散度可以由图中A、B、C、D、E和F六个点之差近似获得

也即

这里的g_xA~g_zF是球体表面不同点的相应的加速度向量的分量。因为小球体中的物质是均一的，所以球体内部的密度被认为是个常数。因此，这六个点的向量均指向球体中心，并且可以由通用的球体引力公式得到

结合万有引力定律，考虑到体积为V=4πδr³/3的球体中的平均密度为ρ=δm/V=3δm/4πδr³，在δr趋近于零的条件下，可以得到泊松方程

应该注意到我们的推导是被简化的，并且用了球体表面的引力加速度的标准描述。高斯定理的基本原理也显示了不仅仅是一个球形，任意形状的局部物质都会得到相同的泊松公式。在一个连续媒介中，密度的分布与此媒介中重力场紧密相关。根据前面的推导，泊松方程就可用以表述此种关系。也就是说，泊松方程描述了一个自主受力的连续体中的重力势能的空间变化

其中，ρ_(x,y,z)是空间密度函数。

图像的泊松编辑

前面推导出了引力加速度场中的泊松公式，各物理量的关系下图所示，下面将这其中的概念平行地转移到数字图像中。理解其中的对应关系是非常有意义的。这部分的讨论综合运用了许多数学知识，除了场论中的哈密尔顿算子和拉普拉斯算子以外，变分法基本方程在这部分的理论推导中也占据着非常重要的位置。

对于一组数字信号而言，它的能量在时域上主要是指它的振幅。而这种振幅对应到图像中，其实就是指各像素的灰度值。所以一幅图像的势能对应的就是原图像自身。对势能求梯度，可以得到相应的场。在图像处理中，可以利用哈密尔顿算子计算原图像的梯度结果，所以这里的场对应的就是图像梯度（注意这里有一个负号）。同理，利用拉普拉斯算子处理原图像，相应得到的就是密度图像。这些概念的对应关系如下图所示。注意到此图中的梯度图像有两张，这是因为可以对原图从水平和垂直两个方向计算梯度。

泊松方程之于图像处理的一个重要应用就是进行图像合成。图像合成是图像处理的一个基本问题，其通过将源图像中一个物体或者一个区域嵌入到目标图像生成一个新的图像。在对图像进行合成的过程中，为了使合成后的图像更自然，合成边界应当保持无缝。但如果原图像和目标图像有着明显不同的纹理特征，则直接合成后的图像会存在明显的边界。针对此问题，法国学者帕特里克·佩雷斯（Patrick Pérez）等提出了一种利用构造泊松方程求解像素最优值的方法，在保留了源图像梯度信息的同时，可以很好的融合源图像与目标图像的背景。该方法根据用户指定的边界条件求解一个泊松方程，实现了梯度域上的连续，从而达到边界处的无缝融合。

泊松图像编辑的主要思想是，根据原图像的梯度信息以及目标图像的边界信息，利用插值的方法重新构建出和成区域内的图像像素。如图上所示，其中u表示原图像中被合成的部分，V是u的梯度场，S是合并后的图像，Ω是合并后目标图像中被覆盖的区域，∂Ω是其边界。设合并后图像在Ω内的像素值由 f 表示，在外的像素值由 f*表示。
注意到图像合并的要求是使合并后的图像看上去尽量的平滑，没有明显的边界。所以，Ω内的梯度值应当尽可能的小。因此，f 的值可以由下式确定

面对上述积分型极值问题，显然需要使用变分法。在所讨论的问题中，被积函数为

带入二维的欧拉-拉格朗日方程，则有

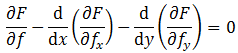
显然F的表达式中不含有f，所以∂F/∂f=0，另外还有

于是得到

另一方面，如果我们要求插入后的图像保持插入图像本身的纹理信息，但是在边界上看不到明显的处理痕迹，此种约束下的优化问题可以表示为

显然，为了使合并后的图像中的Ω区域尽量接近于u，这里利用u的梯度场V作为求解式的引导场。合并后图像在Ω内的像素值f的梯度与u的梯度越接近，就表示原始纹理保持得越好。此时被积函数为

再次应用欧拉-拉格朗日方程，其中

于是得到

再回忆一下之前介绍的散度知识。散度是个标量，对于一个向量场 F=P(x,y)i+Q(x,y)j，它的散度记为div F（或∇∙F），并且有

并可以从散度的角度来定义拉普拉斯算子，此时拉普拉斯算子定义为梯度的散度，即

所以对于二维空间， f 是关于x和y函数，则∆f为

所以原式可以写成下列泊松方程的形式

再回过头看之前的图示，可见上式的物理意义是非常明晰的，即

这也就是泊松图像编辑（Poisson Image Editing）^[2] 和泊松图像融合（Poisson Matting）^[3] 的共同的数学基础。请注意，这一部分内容主要在文献【2】中被首次提出，而在文献【3】中提出的Poisson Matting涉及到求解alpha值的问题，但其本质仍然是上面我们所分析和介绍的这部分内容，理解上述原理对于正确解读文献【3】至关重要。

 

参考文献

【1】  厦门大学偏微分方程公开课（谭忠教授主讲） 
【2】 P. Pérez, M. Gangnet, and A. Blake, Poisson Image Editing. SIGGRAPH 2003. 
【3】 J. Sun, J. Jia, C. K. Tang, H. Y. Shum, Poisson Matting. SIGGRAPH 2004. 
【4】 Kun Zhou, et al., Poisson Mesh Editing. SIGGRAPH 2004. 
【5】  https://wenku.baidu.com/view/a15366ec0975f46527d3e1c3.html