TensorFlow笔记:激活函数
tf.nn.sigmid()函数
函数表达式
f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1
函数图像
函数性质
对其求导可得到 f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f'(x) = f(x)(1 - f(x)) f′(x)=f(x)(1−f(x))
sigmoid函数取值范围在 (0, 1) 区间内,常用于输出层进行二分类
sigmoid函数之前使用很广泛,但因为sigmoid函数的特点,也存在一些缺点
- 在输入点远离零点时,其梯度就会变得很小,在反向传播中容易出现梯度消散
- 函数的输出得到的值永远为正,均值非零,这在前向传播中算是一种缺陷
tf.nn.tanh()函数
函数表达式
f ( x ) = e x − e − x e x + e − x = 1 − e − 2 x 1 + e − 2 x f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} = \frac{1 - e^{-2x}}{1 + e^{-2x}} f(x)=ex+e−xex−e−x=1+e−2x1−e−2x
函数图像
函数性质
对其求导可得到 f ′ ( x ) = 1 − ( f ( x ) ) 2 f'(x) = 1 - (f(x))^{2} f′(x)=1−(f(x))2
tanh又称为双曲正切函数,函数取值范围在 (0, 1) 区间内,可以看做对sigmoid函数做了拉伸和平移,解决了sigmoid均值不为零的特点
tf.nn.relu()函数
函数表达式
f ( x ) = m a x ( 0 , x ) f(x) = max(0, x) f(x)=max(0,x)
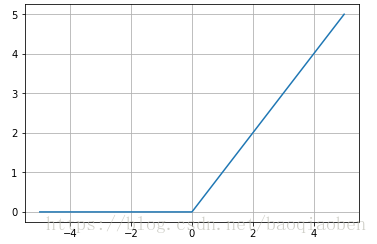
函数图像
函数性质
relu函数对线性函数小于零的部分进行了修正,其优点有梯度计算方便,并且在输入为正时不会产生梯度消散
但是当输入小于零时,对应的神经元输出为零,及不被激活的状态,并且该节点的梯度也随即变为零,造成神经元死掉( die )
因此在使用relu作为激活函数时,learning_rate 的设置很重要,通常不能太大
tf.nn.leaky_relu()函数
函数表达式
f ( x ) = { α x x < 0 x x ≥ 0 f(x) = \begin{cases} \alpha x & x < 0 \\ x & x \geq 0 \\ \end{cases} f(x)={αxxx<0x≥0
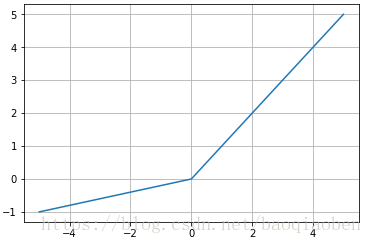
函数图像
函数性质
leaky_relu是对relu函数小于零的部分进行了修正,为其提供了一个较小的导数 α
对于其中的 α 参数,通常是通过先验知识人工赋予一个值。但是如果将其作为一个参数进行训练,则得到了另一个激活函数prelu,此处就不介绍了。