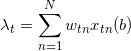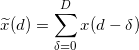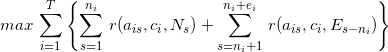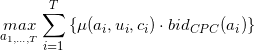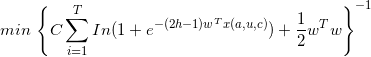计算广告——读书笔记（二）
目录
一、计算广告技术概述
1. 个性化系统框架
2. 各类广告系统优化目标
3. 计算广告系统框架
3.1 广告投放引擎
3.2 数据公路高速
3.3 离线数据处理
3.4 在线数据处理
4. 计算广告系统主要技术
5. 用开源工具搭建计算广告系统
二、基础知识准备
1. 信息检索（Information Retrieval，IR）
1.1 倒排索引
1.2 向量空间模型
2 最优化方法
2.1 拉格郎日法与凸优解
2.2 下降单纯形法
2.3 梯度下降法
2.4 拟牛顿法
2.5 Trust-Region方法
3. 统计机器学习
3.1 最大熵与指数族分布
3.2 混合模型和EM算法
3.3 贝叶斯学习
4. 统计模型分布式计算优化框架
三、合约广告核心技术
1. 广告排期系统
2. 担保式投送系统
2.1 流量预测
2.2 频次控制
3 在线分配
3.1 在线分配问题
3.2 在线分配问题举例
3.3 极限性能研究
3.4 使用优化算法
四、受众定向核心技术
1. 受众定向技术分类
2. 上下文定向
2.1 半在线抓取系统
2.2 文本主题挖掘
3. 行为定向
3.1 行为定向建模问题
3.2 行为定向特征生成
3.3 行为定向决策过程
3.4 行为定向的评测
4. 人口属性预测
五、竞价广告核心技术
1. 竞价广告计价算法
2. 搜索广告系统
2.1 查询扩展
2.2 广告放置
3. 广告网络
4. 广告检索
4.1 布尔表达式
4.2 相关性检索
5. 点击率预测
5.1 点击率预测模型
5.2 优化算法
5.3 点击率模型的校正
5.4 点击率模型的特征
5.5 点击率模型评测
5.6 智能频次控制
6. 探索与利用
6.1 UCB方法
6.2 考虑上下文的bandit
在计算广告——读书笔记（一）中，主要从产品角度介绍，而本篇从技术角度，继续介绍广告业务。
一、计算广告技术概述
1. 个性化系统框架
一般个性化系统由四部分组成：用于实时响应请求，完成决策的在线投放（online serving）引擎，离线的分布式计算（distributed computing）数据处理平台，用于在线实时反馈的流计算（stream computing）平台，链接和运转以上三部分数据流的数据告诉公路（data highway）。
各个个性化系统由于其数据来源、产品形态、优化目标不同，细节上也会呈现不同。以个性化推荐、计算广告和搜索系统为例，如下。
| 搜索 | 搜索广告 | 展示广告 | 个性化推荐 | |
| 主要准则 | 相关性 | 利润 | 用户兴趣 | |
| 其他目标 | 垂直领域决定 | 质量、安全性 | 多样性、新鲜度 | |
| 索引规模 | 十亿级 | 百万级、千万级 | 百万级 | 百万级、亿级 |
| 个性化 | 较少个性化需求 | 亿级规模用户的个性化 | ||
| 检索信号 | 较明确 | 较分散 | ||
2. 各类广告系统优化目标
广告优化的目的是提高广告产品的利润：
在广告系统中，每次展示的 r 是由在线的投放引擎来决策的，而离线数据处理平台和流计算平台所做的都是为了准备
这三个变量或其组合的一些特征。主要广告产品优化目标分解：
| 广告投放 | 产品( ) |
投入( ) |
约束 | |
点击率( ) |
点击价值() |
|||
| GD | 常数 | 常数 | 合约的展示量要求 | |
| ADN |  |
 |
 |
无 |
| ADX | |
|
带宽、服务成本 | |
| DSP | |
 |
 |
预算限制 |
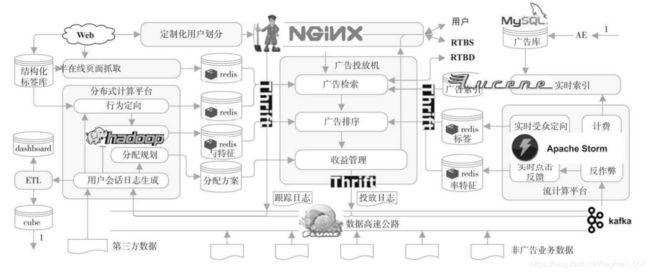
3. 计算广告系统框架
广告系统的建立应该是循序渐进的，对一个刚起步的广告产品，有广告投放机和相应的日志系统，实现简单的定向投放逻辑，就可以开始使用。随着对广告效果深入优化的需求，需要建立起完整的广告排序和用户行为反馈模型；而当中小广告主大量增加时，就需要实现广告的倒排索引和相应的检索功能。
3.1 广告投放引擎
广告系统的投放引擎采用类搜索的架构，即检索加排序的两阶段决策过程。
广告投放机器（ad server）
接受广告前端 Web 服务器发来的请求，完成广告投放决策并返回最后页面片段的主逻辑。广告投放机的主要任务是与其他各个功能模块打交道，并将它们串联起来完成在线广告投放决策。最重要的指标是每秒查询数（Query per Second，QPS）以及广告决策的延迟（latency）。
广告检索（ad retrieval）
在线时根据用户标签（user attributes）与页面标签（page attributes）从广告索引（ad index）中查找符合条件的广告候选。
广告排序（ad ranking）
是在线高效地计算广告的 eCPM，并进行排序的模块。eCPM 的计算主要依赖于点击率估计，这需要用到离线计算得到的 CTR 模型和特征（CTR Model&Features），有时还会用到流计算得到的实时点击率特征（real-time features）。在需要估计点击价值的广告产品（如按效果结算的 DSP）中，还需要一个点击价值估计的模型。
收益管理（yield management）
在各种广告系统中将局部广告排序的结果进一步调整，以全局收益最优为目的做调整的功能，如 GD 系统中的在线分配、DSP 中的出价策略等。
广告请求接口
定制化用户划分（customized audience segmentation）
由于广告是媒体替广告主完成用户接触，那么有时需要根据广告主的逻辑来划分用户群，这部分也是具有鲜明广告特色的模块。
3.2 数据公路高速
3.3 离线数据处理
用户会话日志生成、行为定向、上下文定向、点击率建模、分配规划、商业智能、广告管理系统
3.4 在线数据处理
在线反作弊、计费、在线行为反馈、实时索引
4. 计算广告系统主要技术
特征提取、eCPM估计（点击率预估）、在线分配、强化学习（reinforement learning）、个性化推荐（效果类DSP重定向
5. 用开源工具搭建计算广告系统
nginx+zookeeper+lucene+thrift+flume+hadoop+redis+storm+spark
二、基础知识准备
1. 信息检索（Information Retrieval，IR）
为了达到面向大量中小广告主时良好的扩展性能，计算广告采用的是类搜索的技术框架，即检索加排序两端决策过程。
1.1 倒排索引
倒排索引（inverted index）是现代搜索引擎的核心技术之一，其核心目的是将从大量文档中查找包含某些词的文档集合这一任务用O（1）和O（log n）的时间复杂度表示，其中n为索引中的文档数目。
case有如下几篇文档
D0=“谷歌地图之父跳槽 Facebook”
D1=“谷歌地图之父加盟 Facebook”
D2=“谷歌地图创始人拉斯离开谷歌加盟 Facebook”
D3=“谷歌地图创始人跳槽 Facebook 与 Wave 项目取消有关”
D4=“谷歌地图创始人拉斯加盟社交网站 Facebook”
这些文档中包含的关键词（term）有：{谷歌，地图，之父，跳槽，Facebook，加盟，创始人，拉斯，离开，与，Wave，项目，取消，有关，社交，网站}。首先，去掉“与”这样的没有实际表意作用的停止词（stop word），我们对每一个词建立一个链表，表中的每个元素都是包含该词的某篇文档的标识。于是，与上面的文档集对应的倒排索引，也就是所有关键词的倒排链集合可以表示如下：
谷歌→{D1，D2，D3，D4，D5}，地图→{D1，D2，D3，D4，D5}，之父→{D1，D2，D4，D5}，
跳槽→{D1，D4}，Facebook→{D1，D2，D3，D4，D5}，创始人→{D3}，
加盟→{D2，D3，D5}，拉斯→{D3，D5}，离开→{D3}，Wave→{D4}，
取消→{D4}，项目→{D4}，有关→{D4}，社交→{D4}，网站→{D4}。
倒排索引类结构派生于hash map，其中key为term，引入模板参数来繁华数据类型，value是倒排链，由索引条目组成的链表，索引条目两个域（文档ID和辅助变量，用于表示目前关键词在文档的TD-IDF）。
倒排索引最基本的两项操作：一是向索引中加入新文档，二是给定一个由关键词组成的查询时，返回对应的文档集合。工程难点在于：如何设计精简的数据结构以节省对内存的使用以及如何实时将新的文档加入倒排索引中。
1.2 向量空间模型
倒排索引技术是大规模信息检索的基石，那么向量空间模型（Vector SpaceModel， VSM）则是信息检索中最基础且最重要的文档相似度度量方法之一。VSM 的核心有两点：文档的表示方法和相似度计算方法。
我们对每个文档采用词袋（Bag of Words，BoW）假设，即用各个关键词在文档中的强度组成的矢量来表示该文档：
其中
一般采用词表中第 m 个词在 d 中对应的 TF-IDF（Term Frequency-InverseDocumentFrequency，词频–倒数文档频率）值，这是一种信息检索中最常见的词强度度量，可以分解为两个量的乘积：一个量是词频（Term Frequency，TF），即某文档中该词出现的次数；另一个量是倒数文档频率（Inverse Document Frequency，IDF），即该词在所有文档中出现的频繁程度的倒数。IDF 的引入是考虑到那些广泛出现在各个文档中的常用词对主题的鉴别力并不强，因而需要降低其权重。
采用 BoW 的文档表示方法，在计算两个文档的相似度时，一般是用其对应矢量的余弦距离：
余弦距离的最显著好处是当两个矢量在尺度上没有归一化时，仍然可以得到比较稳健的结果。
2 最优化方法
最优化讨论的是在给定某个确定的目标函数以及该函数自变量的一些约束条件，求解该函数的最大或最小值的问题。这样的问题可以表示为下面的一般形式：
f(x)是一个关于自变量 x 的目标函数，而 g(x)和h(x)为 x 的矢量函数，对应着一组不等式和等式约束条件，其中
表示矢量 g（x）的每一个元素都小于或等于 0。
2.1 拉格郎日法与凸优解
在实际工程中，带约束优化非常常见，有关带约束优化最重要的方法就是拉格朗日法。引入一个拉格朗日对偶函数（Lagrange dual function）或简称对偶函数：
![L\left ( \lambda ,\upsilon \right )=inf[f(x)+\lambda ^{T}g(x)+\upsilon ^{T}h(x)]](http://img.e-com-net.com/image/info8/25b8eef5159d4b7ba219a922188978fb.gif){kind=small}
引入的矢量变量
和
称为拉格朗日乘子，对偶函数是一个关于拉格朗日乘子的函数。对应地，有下面的拉格朗日对偶问题（Lagrange dual problem）：
当原目标函数和所有的约束函数都可导时，强对偶问题最重要的性质是使得KKT（Karush-Kuhn-Tucker）条件成立的点可以同时满足原问题和对偶问题最优化的要求。
2.2 下降单纯形法
在有些问题中，f 不可导或者工程上求导代价极大这种情形下，假设函数值是连续的，那就是采用不断试探的方法，在给定多维初始空间上，假设区间内有唯一最小值，按照黄金分割的方法不断缩小区间得到最小值。
2.3 梯度下降法
当f比较容易求导时，基于梯度下降法是首要选择。假设有D维空间自变量
，那么函数f(x)在x点梯度可以写成：
梯度的几何意义是 f 在 x 点函数值上升最快的方向，因此它是一个与 x 维数相等的矢量。利用梯度的优化方法概念上就是每次都沿着梯度的相反方向按某步长前进一小步，这样的方法称为梯度下降法（gradient descent），其更新公式为：
控制着沿梯度负方向下降的速度，称为学习率（learning rate）。
梯度下降法每次迭代都要用到训练集所有数据，在数据规模较大时，这种方法迭代计算效率低。随机梯度下降（Stochastic Gradient Descent，SGD）的方法每一次迭代并不是精确地计算梯度，而是基于随机选取的一个样例来计算梯度。
从计算角度来看，SGD 并不容易并行实现，为了实现其并行计算，产生了一系列并行 SGD 算法和相应的机器学习框架，如 Parallelized SGD等。
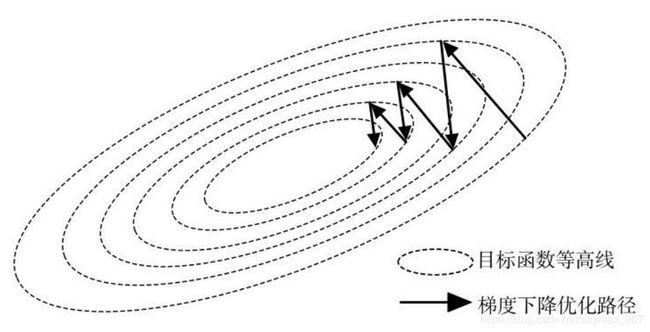
2.4 拟牛顿法
在实际的工程问题中，简单地采用批处理模式的梯度下降法有时会遇到一个麻烦：当函数值对各个自变量归一化不够好时，优化过程会陷入 Zig-Zag 折线更新的困境，如下图所示。在自变量维数很高时，这一问题尤为严重。
引入二阶导数信息，以迅速探索到函数值的谷底。f（x）的二阶导数是一个 D×D 的矩阵，其定义为：
这是一个 D×D 的矩阵，我们称之为赫斯矩阵（Hessian matrix）。同时利用梯度和二阶导数做优化，相当于在当前点处进行二阶的泰勒展开，并找到此二次曲面的极小值点，这样的方法称为牛顿法，其更新公式为：
![x\leftarrow x+\epsilon[\bigtriangledown^{2}f\left ( x \right )]^{-1} \bigtriangledown f(x)](http://img.e-com-net.com/image/info8/e9936ef308cd4e16bb589c26a04be01c.gif){kind=small}
2.5 Trust-Region方法
梯度下降法、牛顿法和拟牛顿法都属于线搜索方法，搜索策略可以概括为“先方向，后步长”。Trust-Region 法采用的是一种不
同的搜索策略：每次迭代时，将搜索范围限制在
的一个置信域内，然后同时决定下次迭代的方向和步长；如果当前置信域内找不到可行解，则缩小置信域范围。在每个迭代中，我们要求自变量的差
满足
。为了单次迭代求解的效率，用函数在 附近的泰勒展开
来近似原来的目标函数
。具体说来，每次迭代需要解下面形式子问题：
通过解得的 s 就可以同时获得本次迭代的方向和步长。
为了实现 Trust-Region 优化策略，还需要确定置信半径
的选取。一般来说，可以通过比较模型函数和目标函数的下降量来指导置信半径的选择：
如果 ，说明目标函数值没有改进；若模型函数较真实地逼近了目标函数，我们期望
的值接近于 1；如果的值较小，说明在当前置信域内，模型函数和目标函数差别较大，需要缩小当前的置信域；如果的值较大，可以在下次迭代时适当伸长收敛半径。
3. 统计机器学习
从机器学习的方法可以分为统计方法和非统计方法。非统计的方法种类很多，并且往往最后都归结于一个具体的优化问题，可以通过深入掌握优化理论和算法，比较有效地把握各种非统计类方法。而统计类机器学习方法，虽然也用到最优化方法，但是还有一些在概率框架下系统性的思路。
3.1 最大熵与指数族分布
最大熵（Maximum Entropy，ME）原理：当在某些约束条件下选择统计模型时，需要尽可能选择满足这些条件的模型中不确定性最大的那个。在最大熵的准则下，估计一个概率的优化问题可以表示成：
![s.t. \, E_{p}[f_{d}(x)]=E_{\widetilde{p}}[f_{d}(x)],\, d=1,2,...,D](http://img.e-com-net.com/image/info8/1ca82bf7270244b4b1066a49a36f94d7.gif){kind=small}
其中，
为概率分布
的熵，
为一组特征函数。
3.2 混合模型和EM算法
由于指数族分布是单模态的，因而不适用于分布比较复杂的数据建模。为了解决这个问题，同时又能充分利用到指数族分布的一些方便的性质，工程领域产生了采用多个指数族分布叠加的部分来建模的实用方法，即混合模型（mixture model）。
3.3 贝叶斯学习
模型参数估计方法都是在最大似然准则下进行的。最大似然准则是把模型的参数看成固定的，然后找到使得训练数据上似然值最大的参数，这是一种参数点估计（point estimation）的方法。
在贝叶斯体系下，模型参数
不再被认为是固定不变的量，而是服从一定分布的随机变量。在没有数据支持的情况下，我们对其有一个假设性的分布
，这称为先验分布（prior），而在观测到数据集 
以后，根据数据集上表现出来的似然值（likelihood）
，可以得到调整后的后验分布
。先验分布、后验分布和似然值之间的变换关系如下：
在最大似然体系中，参数估计是根据似然值最大化得到的点估计，而预测过程就利用估计出来的参数计算似然值 
即可。在贝叶斯体系下，参数的点估计为其后验分布所代替，也就意味着参数在估计结果中具有不确定性，于是，在预测过程中，需要用积分的方式将参数的不同可能性都加以考虑，这是两者非常本质的区别。还有一种常见的参数估计方法，即最大后验概率（Maximum A Posterior，MAP）方法，它本质上仍然是点估计方法，只不过同样引入了先验部分对参数作规范化，因此，其参数估计形式上是对贝叶斯后验概率求极值，而预测过程则与最大似然情形一样。
| 模型估计方法 | 参数估计 | 预测 |
| 最大似然方法 |  |
 |
| 贝叶斯方法 | |
 |
| 最大后验概率方法 |  |
 |
4. 统计模型分布式计算优化框架
mapreduce/spark
三、合约广告核心技术
合约广告的关键特征是广告投放的价格和量由双方协商约定。
1. 广告排期系统
按 CPT 结算的广告位合约，媒体一般采用广告排期系统来管理和执行。广告排期系统与我们后面要讨论的各种广告系统都不同，因为它并不是一个个性化系统，也不太需要服务器端的动态决策。
2. 担保式投送系统
与展示量合约对应的广告系统称为担保式投送（Guaranteed Delivery，GD）系统 。
这一系统的核心技术是在线分配的算法，除此之外，还有流量预测和频次控制两项重要技术。
2.1 流量预测
给定一组受众标签组合以及一个 eCPM 的阈值，估算在将来某个时间段内符合这些受众标签组合的条件、并且市场价在该 eCPM 阈值以下的广告展示量。
流量预测一般的方法其实并不是预测，而是根据历史数据的统计来拟合未来的流量。
工程上的主要挑战在于，给定的受众标签组合可能性非常多，不可能将所有这些组合都预先做好统计。可行的思路是将其视为一个反向检索的问题：在一般的广告检索问题中，索引的文档是广告 a，而查询是（u，c）上的标签；而在流量预测问题中，索引的文档由广告 a 变成了每次展示，而文档的内容即是这次展示上的（u，c）上的标签，而查询由（u，c）上的标签变成了广告设置的受众条件。
主要有以下几个步骤：
（1）准备文档。将历史流量中，（u，c）上的所有标签的展示合并为一个供给节点 i，并统计其总流量 si以及这部分流量上 eCPM 的直方图
。这样的每个供给节点作为流量预测反向索引的一篇文档。
（2）建立索引。对上一步生成的每个供给节点建立倒排索引，文档的 terms 即为此供给节点（u，c）上的所有标签。同时，在索引的正排表部分记录 
和 。
（3）查询结果。对一条输入的广告 a，将其限定的标签条件作为查询，得到所有符合条件的供给节点的集合。
（4）估算流量。遍历上一步得到的每个供给节点，对于某个供给节点 i，首先计算其与该广告 a 的 eCPM 即
，然后根据相应的 eCPM 直方图计算 a 能获得的流量。这样，就可以估算出 a 在出价 
情形下近似能获得的流量。
2.2 频次控制
频次，指的是某个用户在一段时间内看到某个或某组广告的曝光次数。
传统广告三打理论（three hit theory）。在互联网广告中，随着某个用户看到同一个创意频次的上升，点击率呈下降的趋势这一点是可以被验证的。
广告主有时会要求根据频次控制（frequency capping）某个用户接触到某创意的次数，以达到提高性价比的目的。
备注：在 CPC 结算的竞价广告中，可以将频次作为 CTR 预估的特征之一，从而隐式地对广告的重复展示进行控制。
频次控制有客户端和服务端两种解决方案，客户端解决方案把某个用户对某个广告创意的频次记录在cookie中，简单易行但扩展性不好；服务端是在后台专门设置用于频次记录和更新缓存，存在高并发读写要求。
3 在线分配
3.1 在线分配问题
供给与需求二部图
在线分配问题有两个主要的挑战：一是要在量的约束下优化效果；二是要实时对每一次展示作出决策。，一般将此问题简化为一个二部图（bipartite graph）匹配的问题。代表广告库存的供给节点（集合记为I，其中某个节点代表的是所有标签都相同的流量库存）和代表广告合约的需求节点（集合记为 A）。
如果某个供给节点的受众标签能够满足某个需求节点的要求，就在相应的两个节点间建立一条连接边。我们把这个二部图记为G=（I∪A，E ），其中 E 为 I 与 A 之间边的集合。任务就是求解由 i∈I 到 a∈A 的分配比例，使得满足供给方和需求方的约束的同时，某个与广告效果相关的目标函数达到最优。
这样的二部图结构实际上假设了在同样一组供给节点和需求节点之间发生的广告展示，其目标函数或回报 r 是没有差别的。r 由
（a，u，c）组合的函数变成了供给节点 i 和需求节点 a 的函数，将其记为 
，目标函数表示为如下的形式：
为供给节点 i 的总供给量，而
中的每个元素表示 分配给合约 a的比例，这就是在线分配问题求解的变量。
需求约束与供给约束
在线分配问题的第一个约束条件是分配给某广告合约 a 的收益要至少等于其约定的量
，这个约束称为需求约束（demand constraint）:
其中
为将供给节点 i 连接到需求节点 a 的单位流量惩罚。
在线分配问题的另一个约束条件是每个供给节点被分配出去的量不能多于其总流量，这个约束称为供给约束（supply constraint）：
问题框架
根据上面讨论，引入供给约束与需求约束，得到下面的在线分配优化问题框架表示：
3.2 在线分配问题举例
在线分配技术并不仅仅适用于 GD 问题，其他典型的问题还有 AdWords 问题、展示广告问题、最大代表性分配（Maximal Representative Allocation，MRA）问题以及广告交易平台中的询价优化问题等。
GD问题
在 GD 合约的情形下，由于按 CPM 售卖广告在所有合约都满足时，如果不考虑合约 a未完成的惩罚，收益是一定的常数。那么 GD 的优化问题可以写成：
AdWords 问题
AdWords 问题，也被称为有预算约束的出价（budgeted bidder）问题，讨论的是在CPC 结算的竞价广告环境下，给定各个广告主的预算，整体化市场营收的问题。其对应的在线分配问题体现为如下的形式：
把这里的供给节点 i 具体想象成搜索广告中的一个关键词。于是，代表的是将关键词 i 的一次点击分配给广告 a 的期望收益，即广告 a 对关键词 i 的出价；为关键词 i 的总点击量；而 
为关键词 i 分配给广告 a 的流量比例。AdWords 问题的优化目标是整个市场的收入最大化；而需求约束的含义是每个广告主的花费应该小于该广告主的预算。
3.3 极限性能研究
极限性能研究的指标主要是某一在线分配策略的有效性。
所谓有效性可以描述如下：如果能够完全确知所有的流量分布情况，那么可以根据全局的信息求得一个分配的最优解；但是由于分配是在线执行，最优解并不一定能达到，如果某种在线分配策略在最差情形下能够达到上述最优解目标函数的†倍，那么我们就说这一分配方案是†-competitive 的。显然，这里的†是一个[0，1]内的数，也就是该分配方案有效性的度量。
根据最优化拉格朗日算符可以表达为：
不进行预测，把每次展示当作一个供给节点，则有
，于是上式的对偶问题为：
![\small [x_{ia},\beta _{a},a_{i}\geqslant 0]](http://img.e-com-net.com/image/info8/711ae55756cd496cb313917bc1d4f3f1.gif){kind=small}
原问题的每个约束条件对应着一个对偶变量，在线分配的一种优化方案有如下的几个步骤：
- 初始化每个需求约束的对偶变量
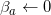
- 当一次展示 i 到达时，令
取得最大值的广告合约 a（即分配给收益最大的合约，如果该值对所有的广告都为负，则所有合约都不需要分配） - 令
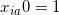，如果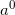
已经被分配了
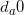次展示，令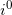 
为其中最小的，并将
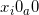设置为 0 - 在对偶问题中，令
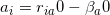，并通过一定的更新规则来更新
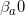。不同的更新规则对应了不同的分配算法，也相应地会导致不同的分配性能
展示分配给最难满足的一个合约：是第 4 步如何更新，有如下几种典型策略：
| 策略 | 描述 | 有效性 |
| 贪心 |  是分配给a的前 个高权重展示中最低的权重，也即a接受一个新的展示需要抛弃的权重 |
1/2-competitive |
| 平均加权 | 是分配给a的前个高权重展示的权重的算术平均，如果分配给a的展示少于个，是这些展示总权重与的比 |
1/2-competitive |
| 指数加权 | 是分配给a的前个高权重展示的权重的指数加权，即设 则：![\small \beta _{a}=d_{a}\left \{ [(1+d_{a}^{-1})^{d_{a}}] \right \}\sum_{j=1}^{d_{a}}r_{j}(1+d_{a}^{-1})^{j-1}](http://img.e-com-net.com/image/info8/29f58cf81d8043e6ba0062ae8892aa7c.gif) |
(1-1/e)-competitive |
可以对应于将一个新的展示替换原有已分配给 a 的展示时，被替换掉的收益部分。
3.4 使用优化算法
假定未来一段时间内需要投放的合约是已知的，如果广告流量的分布在各个循环周期内是近似一致的，那么在线分配的问题就可以在流量预测的指导下进行，这是大多数在线分配实用工程方法的基本出发点。
直接求解的原始分配方案
假定流量的分布是平稳的，我们会利用历史流量数据来拟合未来流量
，把在线分配转化成离线问题。
基于对偶算法的紧凑分配方案
为了分配方案的紧凑性，可否只保留需求约束对应的对偶变量，通过数学变换恢复出供给约束的对偶变量和分配率 x。
综合分配方案 SHALE
采用原始对偶方法迭代进行求解，每次迭代的过程中改善对偶解。
启发式的分配方案 HWM
高水位（High Water Mark，HWM）算法不仅有 紧凑分配、无状态的特性，效果上也能近似最优。
四、受众定向核心技术
1. 受众定向技术分类
从技术框架来看，受众定向标签可以分为用户标签t(u)、上下文标签t(c)和广告主定制标签t(a,u)三种类型。
地域定向、频道定向和上下文定向属于 t（c）的定向方式；人口属性定向、行为定向属于 t（u）的定向方式；而重定向和新客推荐（look-alike）则是 t（a，u）的定向方式。
2. 上下文定向
地域定向、频道/URL 定向、操作系统定向等；另外一类则是根据上下文页面的一些特征标签，如关键词、主题、分类等进行定向，重点讨论这样的上下文定向技术：用规则将页面归类到一些频道或主题分类、提取关键词、主题模型语义映射。
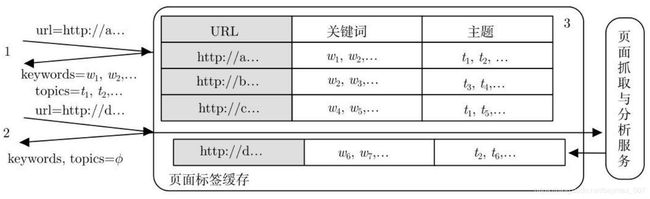
2.1 半在线抓取系统
这一系统的设计关键是不作任何离线抓取，而在在线服务产生实际需求后才尽快抓取。
2.2 文本主题挖掘
文本主题模型有两大类：
- 预先定义好主题的集合，用监督学习的方法将文档映射到这一集合的元素上；
- 不预先定义主题集合，而是控制主题的总个数或聚类程度，用非监督学习的方法自动学习出主题集合以及文档到这些主题的映射函数；
假设有一个由M个词组成的词表以及一组文档
，采用 BoW 表示，文档
表示为
的形式，其中 
为词表中第m个词
在中对应的词频或 TF-IDF 值。显然，一般情况下，矩阵
是非常稀疏的。假设这一文档集合主题模型对应着
这一组主题，我们的目的就是对每个文档得到其在这些主题上的强度
。
LSA模型
文本主题模型最初的解决思路是对上面文档和词组成的矩阵 X 进行奇异值分解（Singular Value Decomposition，SVD），找到这一矩阵的主要模式，这一方法称为潜在语义分析（Latent Semantic Analysis，LSA）。LSA 的分解过程可以表示如下：
其中 K 为矩阵 X 的秩， 为 X 的 K 个奇异值。左侧的矩阵就是将潜在语义空间中的主题映射到某个文档的变换矩阵，而右侧的矩阵则是主题映射到某个文档词表中某个词的变换矩阵。最多可以得到的主题数目等于矩阵 X 的秩 K，不过一般情况下，都会选择一个远小于 K 的主题数目用来建模，如下：
PLSI 模型和 GaP 模型
概率潜在语义索引（Probabilistic Latent Semantic Indexing，PLSI）方法是通过对文档生成的过程进行概率建模来进行主题分析。这一模型下文档生成过程可以表述为：
- 根据每个文档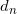生成对应的一个主题 z；
- 给定主题，对应一个词的多项式分布
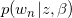，据此生成一个词
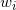；其中的参数
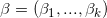，而
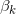即为当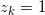
时对应的多项式分布参数；
PLSI 的图模型如下。
对应上面的生成过程，文档集X的生成似然值可以表达为：
其中
为多项式分布 
，显然，这也是一个混合模型的形式，如果
和
也都采用多项式分布形式，就是 PLSI 模型。PLSI 是概率化了的 LSA模型，可以将和的参数分别对应于 LSA 中的两个变换矩阵。
PLSI 模型用多项式分布来描述主题分布和主题中的词分布，而如果采用γ 泊松过程来建模，即假设每个主题生成的概率用独立的 
分布来描述，而主题中某词的产生服从泊松分布，就构成了泊松（GaP）模型。
GaP 与 PLSI 相比，由于没有将每个文档中各个主题变量的强度进行归一化，因此对内容相似的长文本和短文本的概率描述是不同的，而泊松词产生概率也更加适合离散到达事件的描述，因而 GaP 模型在主题建模上有一定的合理性。
LDA模型
在文档信息不足或者噪声较大时能够利用贝叶斯的框架对结果进行有效的平滑，产生了潜在狄利克雷分配（Latent Dirichlet Allocation，LDA）方法。在 LDA 方法中，我们视 PLSI模型的参数为随机变量，对于某一篇文档，其生成过程可以描述如下：
根据一个泊松分布选择文档的长度 M；
根据
的先验分布
生成；
对每个文档中的词
，根据
分布选择一个主题 z；给定主题，对应一个词的多项式分布
，据此生成一个词；
相当于PLSI 的贝叶斯版本。如果采用经验贝叶斯的方法来确定超参数α，那么此时原来的参数ω就变成了隐变量，优化的参数除了α，还包括参数β，优化的目标函数可以写成：
有监督主题模型
无监督的主题模型技术上发展比较充分，但结合广告的业务来看，其得到的主题有时会存在混淆、不易解释等问题。当标签直接用于售卖时，它们往往是预先定义好的。因此，有监督的主题模型对于这种场景更加适用。结合广告定向的场景，可以关注两种有监督主题模型：
有监督的 LDA（supervised LDA，sLDA），这是在某种标签监督下进行主题挖掘的通用模型，适用于标签为各种分布的情形。当标签为离散值时，就对应于根据某种分类进行主题挖掘。
层次化的有监督的 LDA（Hierarchically Supervised LDA，HSLDA）。在此模型中，标注的类型是一个 Hierarchy 上的层次标签，这非常契合于广告中的需求。
3. 行为定向
根据某用户一段时期内的各种网络行为，将该用户映射到某个定向标签上。
3.1 行为定向建模问题
行为定向问题的目标是找出在某个类型的广告上 eCPM 相对较高的人群。如果假设在该类型的广告上点击价值近似一致，那么问题就转化为找出在该类型广告上点击率较高的人群。
点击行为是离散到达的随机变量，对其数量最自然的概率描述是泊松分布。泊松分布的形式如下：
其中 h 为某个用户在某个定向类别广告上的点击量，t 代表某个受众标签，而
为相应的控制点击行为到达频繁性的参数。行为定向模型要做的就是把用户的行为与频繁性参数联系起来。如果利用线性模型联系用户行为和，则有：
这里的
即为标签 t 对应的行为定向模型需要优化的参数，n 表示不同的行为类型，如搜索、网页浏览、购买等。此处将原始行为 b 先经过特征选择函数
，再将结果作为特征用在模型中。
这是工程上一种非常典型的建模思路：当面对一个多自变量的回归问题时，可以先根据目标值的特性选择合适的指数族分布来描述，并用线性模型将多个自变量和指数族分布的参数联系起来。这样做，可以利用线性模型更新简单和可解释性强的特点，同时又对目标变量的类型有较强的适应性。这种建模方法称为广义线性模型（Generalized Linear Model，GLM）。
3.2 行为定向特征生成
行为定向特征生成有两点需要讨论：一是特征选择函数
的确定，一是对应模型的训练集的组织和生成方式。
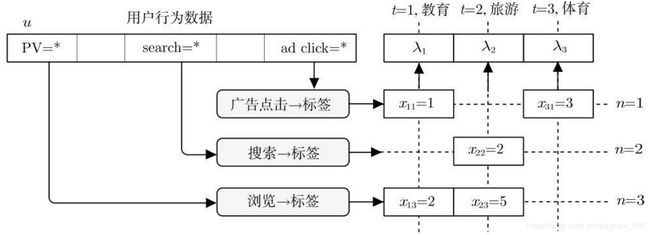
最常用的特征选择函数是将一段时间内的原始用户行为映射到确定的标签体系上，同时计算出各行为在对应标签上的累积强度作为模型的特征输入。
如何将行为累计控制在一段时间以内，工程上有两种常用的方法，分别是滑动窗口法和时间衰减法，如下所示。
滑动窗口法计算公式：
其中，
代表累积特征以区别于单时间片特征
。
时间衰减法计算公式：
从工程角度看，我们更推荐使用第二种方案。
行为定向的训练过程实际上就是调整各个标签类别上各种特征权重的过程。影响训练结果和效率的因素主要有两个：
- 训练集的长度；
- 时间片的大小；
训练集的样本数目正比于训练集长度且反比于时间片长度。当用户数目较多、训练集长度较长，而时间片又较短时，总的训练样本数目是非常大的。
3.3 行为定向决策过程
行为定向计算过程比训练过程的数据准备要简单，因为不再需要准备目标值，只需要按照滑动窗口法或者时间衰减法得到累积特征 再根据加权求和得到得分
。由于这一计算过程也是线性的，当特征累积采用时间衰减法时，得分也可以通过昨天的得分衰减后累积上今天得分的方式得到，即：
在线上存储各用户的定向标签得分的缓存中，在每个新的时间周期，在缓存中得分乘以
进行衰减，再将上一个时间周期收集到的原始行为加权求和后累加上去即可。
3.4 行为定向的评测
行为定向可以通过 reach/CTR 曲线来进行半定量的评测。在正常情况下，较小的人群规模应该较为精准，也即对该类型广告的 CTR 较高；而随着人群规模的扩大，该 CTR 也会逐渐走低。我们把标签接触到的人群规模称为 reach，而这一 reach 和 CTR
构成的曲线是评价该标签上的定向是否合理、以及效果如何的重要依据。
工程中需要注意的是，生成 reach/CTR 曲线的过程需要仅仅访问一遍数据就能完成。因此，在前面受众定向的过程中，需要保留的是每个用户在各个标签上的得分值，而不是最后二元的判断结果。
4. 人口属性预测
在定向广告中，规模化获取人口属性比较困难，往往还是需要数据驱动的模型，以用户行为为基础自动预测其他人口属性。
五、竞价广告核心技术
在竞价广告中，大量中小广告主的检索规模使得计算的效率要求很高，如何根据广告的业务要求设计更高效的索引和检索技术是竞价广告系统要解决的关键问题。
另外，竞价广告系统还需要对给定（a，u，c）组合上的 eCPM 做尽可能准确的估计，由于大量中小广告主的参与，广告系统对 eCPM 的估计往往面临样本不足的情形。
结合广告业务的特点设计有效的特征，让点击率模型快速捕捉用户兴趣的动态信号是提高点击率预测效果的关键。
在搜索广告中，竞价标的即关键词的粒度很细。因此，查询扩展问题至关重要。
搜索广告的北区广告条数在策略上存在非常大个性化调整空间。
1. 竞价广告计价算法
对于一个 CPC 结算的竞价广告系统，需要先得到广告候选集合，并计算每个候选的点击率，这对应了竞价广告两个最关键的计算问题：广告检索和广告排序，这也是本章要讨论的重点技术问题。
竞价广告中根据 eCPM 对广告进行排序，按照点击和转化两个发生在不同阶段的行为，eCPM 可以分解成点击率和点击价值的乘积，eCPM 的估计主要就是点击率预测和点击价值估计两个任务：
点击率µ是广告三个行为主体的函数，而点击价值则是用户 u 和广告商 a 的函数。在CPC 计算的竞价广告中，点击价值是广告主的出价，不需要估计。
2. 搜索广告系统
搜索广告的优化目标，可以用下式表示：
对每次展示的各个候选，根据查询估计其点击率µ，并乘以广告主出的点击单价得到 eCPM，再按此排序即可。搜索广告的检索过程一般都不考虑用户u的影响，而上下文信息 c，即查询，又是实时通过用户输入获得，因而离线受众定向的过程基本可以被省略。
2.1 查询扩展
搜索广告中查询的重要性极高，粒度又非常细，如何根据广告主需求对关键词进行合理的拓展对于需求方和供给方来说都有很大意义。需求方需要通过扩展关键词获得更多流量；供给方则需要借此来变现更多流量和提高竞价的激烈程度。
基于推荐的方法
利用搜索日志把用户一个会话（session）内的查询（query）视为目的相同的一组活动，可以在{session，query}矩阵上通过推荐技术产生相关的关键词。
给定一组用户会话
和一组关键词
，可以产生一个对应的交互强度矩阵
。如果其中某个用户搜索过某个关键词，则矩阵相应的元素就置为一个相应的交互值，比如该用户在一段时间内搜索过该词的次数。类比根据群体用户的选择关联性进行推荐的问题（协同过滤，CollaborativeFlittering，CF）问题。
基于主题模型的方法
除了利用搜索的日志数据，也可以利用一般的文档数据进行查询扩展。这类方法实质上就是利用文档主题模型对某个查询拓展出主题相似的其他查询。
在主题模型的描述下，每个词 wn都可以对应于一个文本主题组成的矢量
。于是，也可以用两个词对应的主题矢量来计算它们相似度。主要考虑的是语意上的相关性，而非用户意图上的相关性，因此效果会差一些。
基于历史效果的方法
对搜索广告而言，还有一类查询扩展方法很重要，那就是利用广告本身的历史 eCPM数据来挖掘变现效果较好的相关查询。某些关键词对某些特定广告主的 eCPM 较高，eCPM 来指导查询扩展，往往能够成为前两种方法非常重要的补充手段。
2.2 广告放置
考虑到用户体验，需要对北区广告的数量进行限制，是一个典型的带约束优化的问题：约束是系统在一段时间内整体的北区广告条数，而优化的目标则是搜索广告系统的整体营收。可以表述为：
其中 
和
分别表示第 i 次展示的北区和东区广告条数。在 eCPM 的表达 r 中，多了一个表示位置的参数。例如，
表示北区的第 s 个位置，
表示东区的第 s 个位置。C 为北区的平均广告条数上限。
这个问题形式上不是可导的，而且要调整的参数也不太多，可以采用最优化方法中介绍的下降单纯形法求解。
搜索广告虽然不宜进行深入的个性化，但在广告放置问题上存在着很大的个性化空间。对不同的用户动态调整北区的条目数可以使得在北区平均广告数目相同的约束下，整体系统的营收有显著的提高。对于北区的一个广告展示，改成下面的形式：
这里的
和
分别表示用户
对北区广告的平均点击率和所有用户对北区广告的平均点击率。在计算点击率的过程中需要对北区不同位置的点击做归一化，并且需要做平滑。
3. 广告网络
广告网络是除了搜索广告以外最重要的非实时竞价类广告产品。由于没有了明确的用户意图以及展示位置的固定性，像查询扩展、广告放置等问题在广告网络中并不存在。可以用下式表达：
由于广告网络的成本是分成或包断媒体资源；而收入部分是比较典型的根据“a given user in a given context”，求“suitable ad”的过程，即根据给定的用户和上下文求合适的广告的过程。
准实时的计费和点击反作弊功能是必不可少的；另外，将用户行为尽快反馈到广告决策中对于点击率预估和受众定向的效果提升也非常关键。
短视行为反馈与流计算场景：实时反作弊、实时计费、短时用户标签、短时动态特征。
4. 广告检索
大量中小广告主参与的竞价广告市场中，复杂的定向条件对检索技术提出了新的要求。倒排索引是搜索引擎的关键技术，而广告的检索上也采用这样的框架。倒排索引技术在广告检索中遇到了两个新问题：
- 广告的定向条件组合可以看成是一个由与或关系连接的布尔表达式，这样的文档显然与搜索引擎面对的 BoW 文档不太一样，这里存在着有针对性的检索性能优化空间；
- 在上下文关键词或和用户标签比较丰富时，广告检索中的查询可能相当长，甚至会由上百个关键词组成，这种情况下的检索也与搜索引擎中主要由 1～ 4 个关键词组成的查询有很大区别；
4.1 布尔表达式
广告检索与普通搜索引擎检索的第一个不同是布尔表达式的检索问题。用布尔表达式表示广告的定向人群，并且写成析取范式（Disjunctive NormalForm，DNF）的形式。
class Assignment {
public:
int attribute; // 标签类型
bool belong; //属于还是不属于
int value; //指定的标签取值
}
// 一个或多个Assigment的交
typedef vector Conjunction;
// 一个或多个Conjunction的并
typedef vector DNF; 4.2 相关性检索
竞价广告与搜索的检索问题还有一点不同，有时，竞价广告系统需要处理很多个标签组成的查询。
在长查询的检索情形下，我们实际上希望的是查询与广告候选间的相似程度尽可能高，但任何一个关键词是否出现在文档中其实都不关键。这样以查询和文档间的相似程度为目标的检索问题称为相关性检索。
解决相关性检索的基本思路是在检索阶段就引入某种评价函数，并以此函数的评价结果决定返回哪些候选。当选用线性评价函数（变量为各标签或关键词）且各权重为正时，是可以构造出这样的快速检索算法的。假设线性评价函数的形式如下式所示：
其中
和
分别表示广告文档 a 和上下文特征 c 上不为零的特征集合，比如查询中的关键词，而
表示 t 这一特征在 a 广告上的贡献值。
如果不考虑余弦距离中的归一化分母，可以用这一线性函数在检索阶段做近似的预评估。这种情况下，
即为关键词 t 在上下文中的 TF-IDF，而即为t在某广告 a 中的 TF-IDF。
5. 点击率预测
广告点击率预测的目的是广告排序，更适合被建模成回归问题而不是排序问题。
5.1 点击率预测模型
把点击事件 h 看成一个二元取值的随机变量，那么其取值为真（h=1）的概率就是点击率。因此，点击事件的分布可以写成以点击率 µ为参数的二项分布（binomialdistribution）：
点击率预测模型的作用是在（a，u，c）组合与点击的概率
之间建立函数关系，这可以表示成对
的概率建模问题，可以很自然地想到的基础模型是逻辑回归（Logistic Regression，LR）：
其中 x 表示（a，u，c）组合上的特征矢量，即前面介绍过的受众定向的输出及其派生的其他特征；w 为各特征的加权系数，也就是此模型需要优化的参数；
这一线性函数的输出经过逻辑 S 型 Sigmoid 函数
映射到（0，1）区间内，其中（2h−1）是为了将 {0，1} 的点击变量变换到集合 {−1，1} 上。
实践中，由于 LR 模型使用的特征较多，并且有相当多的特征在训练集中出现的次数并不多，为了避免过拟合，还需要在最大似然估计时加入正则化项。如果采用 L2-norm，则此优化问题可以表达成：
5.2 优化算法
对于 LR 模型，我们通常采用最大似然估计来求解加权系数 w。
L-BFGS
拟牛顿法在点击率预测这样的特征维度很高的优化问题中，赫斯矩阵的尺寸过大，根本无法在内存中存放。解决这一问题的思路是仅仅保留最近几次更新的一些状态矢量，然后利用这些状态矢量和当前的梯度，直接计算出更新方向，这种方法称为有限内存 BFGS（Limited-memoryBFGS，L-BFGS）。
Trust-Region 法
对于这样高维的问题，可以采用共轭梯度法（conjugate gradient method）来求解Trust-Region 的子问题。
5.3 点击率模型的校正
点击率预测问题有一个数据上的挑战，就是正例和负例样本严重不均衡，特别是在展示广告点击率只有千分之几的情况下。
点击率模型可能存在偏差的原因如下图所示。假设分别用两个高斯分布来描述 h=0和 h=1 情形下的特征分布。由于 h=1 时的数据量远远小于 h=0时的数据量，对前者的方差低估就会更严重，前者的分布（右侧的高斯分布）会变得更窄一些，也就意味着更多的样本被分到了 h=0 这个类中，或者说意味着点击率将会被系统性地低估一些。
5.4 点击率模型的特征
点击率预测问题的主要挑战在于如何使模型能捕捉高度动态的市场信号，以达到更准确预测的目的。这一挑战可以用在线的模型学习算法，或者用快速更新的动态特征来解决。将重点放在第二种思路，因为其工程扩展上更方便一些。
静态特征
静态特征都是取值为 0 或 1 的特征。
动态特征
采用这个组合历史上一段时期的点击率作为其特征取值。可以这样理解：
最终预测的是某个特定（a，u，c）上的点击率，而某个组合特征 t（a，u，c）上的点击率可以认为是关于最终目标的一个弱决策器。通过对这些对应特征组合的弱决策器的融合，可以更容易地预测该（a，u，c）上的点击率。
位置偏差与CoEC
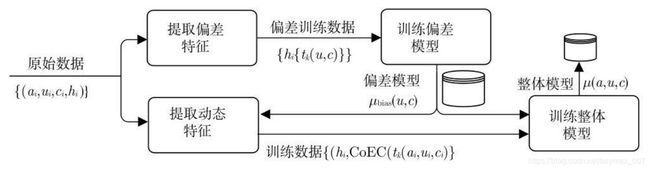
一些非定向因素对点击率有比较大的影响，主要的有广告位位置、广告位尺寸、广告位类型（如门户首页、频道首页、内容页、客户端）、创意类型（如图片、Flash、富媒体）、操作系统、浏览器、日期和时间等。所有这些因素，都与广告决策没有关系，但是对点击率的影响要远远超过定向技术带来的影响。
如何去除位置等因素的影响呢？工程上一种合理的办法是将某广告位相当长一段时期内的平均点击数作为其关注程度的近似评估，我们把这一指标称为期望点击（expected click，EC）。
只用那些偏差因素作为特征，训练一个点击率模型，这个模型称为偏差模型（bias model）。这里的偏差因素指的是那些与广告决策无关的特征，这些特征一般来说与广告 a 无关。偏差模型可以概念性地表示为：
偏差模型需要用比一般点击率模型更长时间的数据来训练，这样做的目的是希望消除某段时期广告质量带来的影响。
得到了偏差模型以后，可以定义下面的归一化的点击率指标：
这一指标是点击与期望点击的比值，因此称为 CoEC（Click on Expected Click）。由于在分母上考虑了位置以及其他因素的偏差对点击率的影响，这一指标可以更准确地表征某部分流量上广告投放的实际点击率水平，也比较适用于点击反馈这样的动态特征。
- 采用动态特征和偏差模型的工程方案，点击率预测模型训练的流程分三步完成：
- 用较长一段时间的训练数据，只提取偏差特征并训练偏差模型；
- 利用得到的偏差模型计算所需维度组合上的 CoEC 作为动态特征；
- 用所有非偏差的动态特征训练整体点击率模型，其中用偏差模型的输出作为点击率的先验；
点击反馈的平滑
用 CTR 或 CoEC 这样的点击反馈作为动态特征，大量的长尾组合特征对于准确地预测点击率有很大帮助。但是要利用好这些长尾组合特征，还需要解决一个问题，就是在统计不足的维度组合上如何稳健地统计 CTR 或 CoEC。
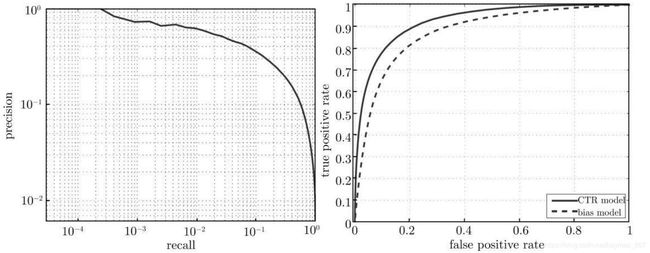
5.5 点击率模型评测
点 击 率 模 型 预 测 的 是 点 击 事 件 出 现 的 概 率 ， 因 此 可 以 采 用 准 确 率 / 召 回 率（Precision/Recall，PR）曲线或接收机操作特性（Receive Operating Characteristic，ROC）曲线来评测。
点击率模型是一个对点击事件进行预测的模型，因此，对任何一个样本实例，存在下面四种情况：
- 点击行为被预测为点击行为，其数目计为
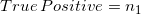； - 点击行为被预测为非点击行为，其数目计为
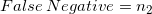； - 非点击行为被预测为点击行为，其数目计为
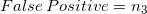； - 非点击行为被预测为非点击行为，其数目计为
；
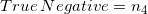通过取不同的阈值，就可以得到一条Precision/Recall 曲线或者是 True Positive Rate/False Positive Rate 的曲线，前者即为
PR 曲线，而后者就是 ROC 曲线。
PR 曲线呈下降的趋势，不过这并没有理论上的保证，实际数据上局部呈上升趋势的 PR 曲线也很常见。对广告而言，应该更加关注 PR 曲线的头部，因为尾部是 Recall 比较高，也就是很多广告候选都被考虑时的情形，而实际的投放环境中，只选择排名最好的一个或几个候选。
ROC 曲线呈上升的趋势，不过这一点同样没有理论上的保证。与 PR 曲线不同，ROC 曲线下的面积有明确的物理意义，它在一定程度上表征了对 h=0 和 h=1 事件估计值排序的正确性。我们把 ROC 曲线下的面积称为曲线下面积（Area Under Curve，AUC），这是评价点击率模型时常用的量化指标。
5.6 智能频次控制
在广告网络情形下，由于广告主的创意可能出现在各种媒体的各种位置上，不同位置的有效展示有相当大的差别。因此，简单设定一个展示数目上的频次来控制用户的接触次数是不太合理的。
EC 从某种程度上更接近于有效展示数目，可以采用 EC 上的累积计数代替频次来控制用户接触次数。
6. 探索与利用
对某种类型的（a，u，c）组合，如果没有相关历史数据的支持，很难对其合理地估计点击率。由于线上我们总是使用统计上最优的策略来投放广告，那些非最优的组合出现机会很少，因而对这部分的估计也就不准确。无法对特征空间均匀采样构造训练集，是互联网问题区别于其他机器学习问题的重要特点。
采用相对随机的策略采样那些效果未知的特征空间，这称为探索（exploration）过程；再根据探索和正常决策的总体流量更有效地预测点击率，这称为利用（exploitation）过程。这样整体策略称为探索与利用，即 E&E。
类比问题——多臂老虎机（Multi-Arm Bandit，MAB）：玩家面对老虎机上 A 个有不同期望收益的手柄，需要用尽可能少的筹码探索出收益最高的那个手柄，然后利用这个结果去获取回报。
6.1 UCB方法
MAB 问题经典的思路是置信上界（Upper Confidence Bound，UCB）方法。此方法在每次投放时不是简单地选择经验上最优的广告，而且考虑到经验估计的不确定性，进而选择估计值有可能达到的上界最大的那个广告。
UCB 的过程主要分成两个步骤：
- 首先根据过去的观测值，利用某种概率模型计算出每个 a 的期望回报的 UCB；
- 选择 UCB 最大的 a；
6.2 考虑上下文的bandit
对于需要探索的空间过大的问题，工程上比较常用的思路是将此空间参数化，在一个维数较低的连续空间中进行探索。这样的 E&E 问题可以称为考虑上下文的 bandit（contextual bandit）问题。
考虑上下文的 bandit 的问题，代表性的思路有 LinUCB 方法。