2017国庆郑州集训游记Day3
字符串 Hash
···字符串 Hash:一种从字符串到整数的映射
···通过这样的映射,把比较两字符串是否相同转化为两整数是否相同
····若比较发现两字符串hash值相等,我们认为两字符串很大可能是相同的
····另一方面,若 hash 值不等,则两字符串一定不同
····比较字符串 O(L),比较整数 O(1)
BKDR-Hash
··竞赛中常用的 hash 策略
··把字符串视为一个 base 进制的大整数,对某个质数 P 取模得到 hash 值
··sum_i = (sum_{i-1} *base + str_i) mod P
··base 可以取 31、131、13131 等,需要满足 base > |字符集|
··P 取 long long 范围内一个质数,注意溢出问题
··使用 unsigned long long 自然溢出可以视为对 2^64 取模
(电脑自动取最低的64位 即为自动取模)
··但是可能被卡(对任意base)
··害怕 Hash 被卡的同学,也可以选择双 hash(常数翻倍
常用技巧
····给定字符串 S,预处理出它的前缀 Hash 函数;同时计算好 mod P 意义下 base 的幂次表
····sum[i] = (sum[i - 1] * base + str[i]) % P
····pw[i] = (pw[i - 1] * base) % P
····基础应用:
··提取一段子串的 hash 值
··合并两个串的 hash 值
··O(\log n) 计算两个子串的 lcp 和字典序大小
想提取【l,r】的哈希值:
【l,r】=s(r)-s(i-1)*10^(l+r-1)
eg:
企鹅QQ
给定 N 个长度均为 L 的串
问有多少对字符串满足:恰好有一位对应不同
N <= 30000, L <= 200
解:枚举删掉每一个位置,用 Hash 来进行答案统计
Trie 树
又称字母树,可以用来维护字符串集合
优化思想是,利用字符串的公共前缀来减少查询时间,最大限度地减少无意义的比较
结构:有根树,每条边上存有一个字符
从根到每个叶子的路径上经过的字符写下来,对应了一个字符串
无敌伪代码:
namespace Trie
{
struct node
{
int ch[26];
//other info
}t[Max_M];
int Root,pookCur;
void inti()
{
Root=1;
poolCur=2;
}
inline int newnode()
{
int o=poolCur++;
memset(&t[o],0,sizeof(node));
return poolCur++;
}
int insert(char s[],int n)//s[0..n-1]
{
int o=Root;
for(int )
}
}
支持的操作:插入、查找、删除
例 1
给定 2 * N 个字符串,你需要将它们配对起来
两个字符串 x、y 配对的得分是它们的 lcp 长度
最大化得分
N <= 10^5,字符串总长 <= 2 * 10^6
解:建出 trie 树,两个串的 LCP 即为它们的 LCA 的深度
使用贪心算法,按照树的 DFS 序列配对
(树的DFS序列如图)
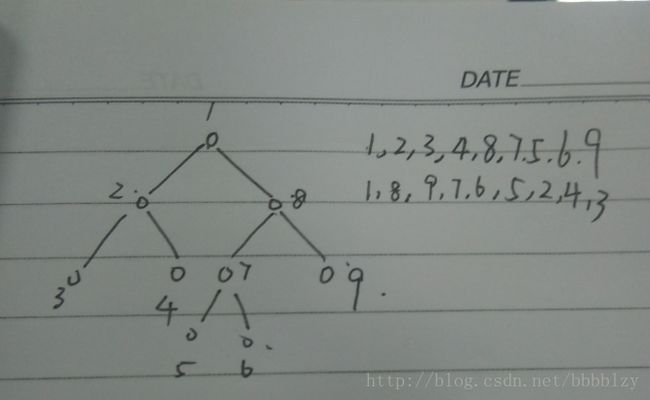
例 2
给定一棵有根树,每条边有权值 w_i
求树上的一条简单路径,使得路径经过的边权异或和最大
N <= 2 * 10^5, w_i <= 10^9
解:
记录 dis[a] 表示 a 到根的链的异或和
考虑 x、y 之间的链的异或和,设 LCA 为 z
= (dis[x] ^ dis[z]) ^ (dis[y] ^ dis[z]) = dis[x] ^ dis[y]
不难发现与 z 无关!
于是问题转化为,给定 N 个数,选出两个使得异或和最大
解 cont’d:
考虑枚举两个数之一 x,我们想在其它数中找到一个与 x 的异或和最大
从高到低考虑每一位,尽可能让更高位为 1
不难发现可以使用 Trie 树!
复杂度 O(N * 32)
并查集
维护 N 个集合,初始时第 i 个集合为 { i }
支持两个操作:
把两个集合合并起来
查询两个元素是否在同一集合
N <= 10^6
原理:
对每个集合,建立一个有根树的结构
令树的根为整个集合的“代表”
想知道两个元素是否在同一集合,只需比较它们的代表
合并时,将一棵树接到另一棵下边即可
优化策略
路径压缩 按秩合并(把小的并到大的里面去)
可以证明,使用这两种优化的并查集复杂度为 O(α(n)) 绝大多数情况这个值不大于 5,可以认为是线性的
应用
最小生成树的 Kruskal 算法
Tarjan’s off-line LCA Algorithm
带权:
在一些应用中,可以在每个点上额外维护一些信息,表示“它与父亲”之间的关系
进而尝试推算集合中任意两个元素之间的关系
例:
某市有两个帮派,有 N 个人,每个人属于两个帮派之一。
给定 M 个事件:
1 x y,表示告诉你 x 和 y 属于同一帮派
2 x y,表示告诉你 x 和 y 不属于同一帮派
3 x y,表示请你推理 x 和 y 之间的关系
N <= 5 * 10^5, M <= 10^6
解:
给每个人额外维护一个标记 rel[x] 表示 x 和 x 的父亲的关系
由 rel[x] 和 rel[fa[x]] 可以推算 x 和 fa[fa[x]] 的关系。。。以此类推可以推算 x 和 Root[x] 的关系
于是任意两个人只要在同一连通块,就能推算他们的关系
问题:这个并查集如何使用路径压缩优化呢?
只按秩合并
只按秩合并的并查集,可以在合并的时候一定程度上保留元素合并在一起的 “过程”
看一个经典例题
例
给定 N 个点,支持 M 个操作:
1 x y,在 x 和 y 之间连边
2 x y,询问 x 和 y 是否连通,如果是,那它们最早在哪一次操作之后连通的
N <= 2 * 10^5, M <= 5 * 10^5
解:
@货车运输
离线的时候可以建树倍增 blabla。。。
强制在线呢?
只按秩合并,link(x, y, tim) 时,我们在 Root[x] 和 Root[y] 之间连一条边权为 tim 的边
询问 (x, y) 时,找到 x 和 y 之间边权最大的边即可
这种算法的复杂度是容易证明 O(\log N) 的正确性?
优先队列
支持这样几种操作的数据结构:
插入一个优先级为 key 的元素
询问优先级最高的元素
删除优先级最高的 / 任意一个元素
升高一个元素的优先级值
优先队列一般使用堆来实现
最经典的堆即为大名鼎鼎的二叉堆
二叉堆
二叉堆是一个完全二叉树结构,并且它具有堆性质:
每个点的优先级高于它的两个孩子(如果有)
可以用一个数字来存储二叉堆,避免指针:
1 是根结点
对于 x,它的左右孩子分别是 2x 和 2x+1
容易验证 N 个点的二叉堆,它用到的数组即为 1 ~ N
给定一个大小为 N 的数组,我们可以 O(N) 的建堆(How?
调整
随着操作的进行,二叉堆的“堆性质”可能会遭到破坏,为此我们定义两种调整操作,来维护二叉堆的堆性质保持不变
向上调整:
当一个点的优先级升高时,我们需要向上调整
比较它和它的父亲的优先级,它的优先级高就与父亲交换位置并递归进行
向下调整:
当一个点的优先级降低时,我们需要向下调整
比较它和它左右儿子中优先级较高的那个,它的优先级低就与儿子交换并递归下去
容易验证两种操作的复杂度均为 O(\log N)
操作
插入:插入一个叶子,然后向上调整
询问:返回 a[1]
删除根:令 a[1] = a[N],然后向下调整
左偏树
也是一种优秀的堆
并且是支持合并的(可并堆)
比较简单,容易实现
但是我们不讲
应用
Dijkstra 算法和 Prim 算法的优化
哈夫曼编码
一些奇怪的应用
例 1
给定数轴上 N 个点,你需要选出 2 * K 个,把它们配对起来
把两个点配对起来的花费是它们坐标之差的绝对值
最小化花费
N <= 3 * 10^5
解:
一定是取相邻两点配对
问题可以转化为,选出 K 个相邻点对
进一步转化为,有 N - 1 个线段,选出 K 个,且相邻的不同时选
用堆进行贪心
给贪心一个“修正”的余地:
选了 p[i],把 p[i - 1] + p[i + 1] - p[i] 入堆
例 2
炒股,一共有 2 * N 天,每天有一个买入和卖出价
刚开始时你有 0 支股和充分多的钱
每天要选择买或者卖一支股票(股票数时刻不为负
最后一天结束你要清仓
虽然你有充分多的钱,你还是想知道自己最多能在这些天赚到多少钱
N <= 2 * 10^5
解:转化成括号序列问题?
线段树入门
线段树是一种二叉搜索树,一般可以用来维护序列的子区间
结构
对一个长度为 n 的序列建线段树,根结点即表示 [1, n]
对于一个表示 [l, r] 的节点:
若 l = r,则它是叶子
否则,令 m = (l + r) / 2,它有左右两个孩子,分别记为:[l, m] 和 [m + 1, r]
不难验证,这样一个线段树中有 2N - 1 个节点,并且树的深度是 O(\log N) 级别
原理
线段树的优化思想:
根据问题的要求,用每个节点维护它对应的子区间中、可以高效合并的相关信息
在动态的序列问题中,对于修改操作没有动过的部分。我们可以考虑把这些地方的求解的结果保存并复用,从而达到优化程序效率、降低复杂度的目的。
例 1
给定一个长度为 N 的序列,支持:
修改一个位置的值
查询一个子区间的元素和
解:
线段树每个节点维护对应子区间的和
区间覆盖:
对于一个区间 [l, r],我们可以将其分解为线段树上 O(\log N) 个节点的并;
这里的分解是指,我们选取的区间并起来恰好为 [l, r]。且选择的区间不会相互重叠
修改操作中,为了维护线段树性质,需要修改总共 O(\log N) 个节点
查询操作,将区间拆为 O(\log N) 个区间的并,从而优化查询的复杂度
总时间复杂度 O(\log N)
树状数组
一种支持单点修改和查询前缀和的数据结构
复杂度为 O(\log N),但是常数很小
原理
定义 lowbit(x),表示将 x 写成二进制后,只保留二进制下最低一个 1 对应的整数
例:lowbit(1001100) = 100, lowbit(1000) = 1000
十进制:lowbit(76)=4, lowbit(8) = 8
对一个数组 a[],我们构造数组 c[],其中
c[i] = sum (. a[i - lowbit(i) + 1 … i] )
巧妙的事情来了:
我们查询 a[] 的前缀和只需要访问 c 中 log N 个节点
修改 a[] 中任意一个元素的值,只需要同时修改 c 中的 log N 个节点
于是可以在 O(\log N) 的时间内支持单点修改、前缀和查询
