自然语言处理(NLP)-基于概率最大化的中文分词算法(Java实现)
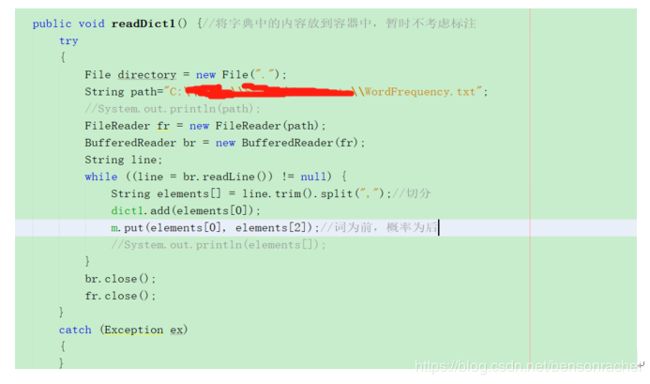
摘要:平台使用Netbeans搭载JDK1.8环境编程。实现基于概率最大化的中文分词算法并集成于一个窗体平台(如下图)。字典使用WordFrequency.txt;
理论描述:
最大概率法分词是在最大匹配分词算法上的改进。在某些语句切分时,按最大长度切分词语可能并不是最优切分。而不按最优长度切分词语,则同一语句会出现多种切分结果。计算每种切分结果的概率,选取概率最高的切分作为最优分词切分。基于动态规划的最大概率法的核心思想是:对于任意一个语句,首先按语句中词组的出现顺序列出所有在语料库中出现过的词组;将上述词组集中的每一个词作为一个顶点,加上开始与结束顶点,按构成语句的顺序组织成有向图;再为有向图中每两个直接相连的顶点间的路径赋上权值,如A→B,则AB间的路径权值为B的费用(若B为结束顶点,则权值为0);此时原问题就转化成了单源最短路径问题,通过动态规划解出最优解即可。利用字与字间、词与词间的同现频率作为分词的依据,不一定需要建立好的词典。需要大规模的训练文本用来训练模型参数。
优缺点:不受应用领域的限制;但训练文本的选择将影响分词结果。
算法描述:
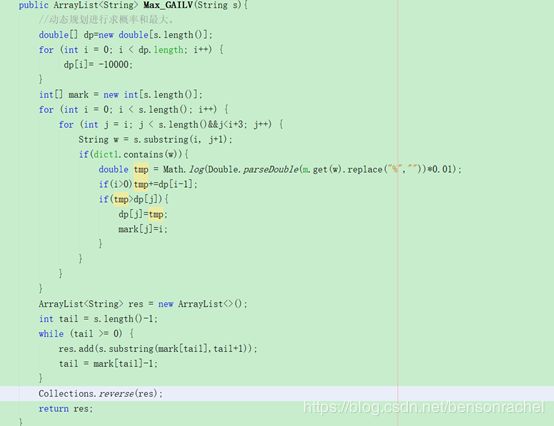
从统计思想的角度来看,分词问题的输入是一个字串C=C1,C2,……,Cn,输出是一个词串S=W1,W2,……,Wm,其中m<=n。对于一个特定的字符串C,会有多个切分方案S对应,分词的任务就是在这些S中找出概率最大的一个切分方案,也就是对输入字符串切分出最有可能的词序列。
① 对一个待分词的子串S,按照从左到右的顺序取出全部候选词w1,w2,…,wi,…,wn;
②到词典中查出每个候选词的概率值 P(wi),并记录每个候选词的全部左邻词;
③按照公式 1 计算每个候选词的累计概率,同时比较得到每个候选词的最佳左邻词;
④如果当前词 wn 是字串 S 的尾词,且累计概率 P(wn)最大,则 wn 就是 S 的终点词;
⑤从 wn 开始,按照从右到左顺序,依次将每个词的最佳左邻词输出,即 S 的分词结果。
关于计算切分概率
- W:所有可能的切分组合
- S:待切分语句
最佳切分:
argmaxwP(W|S=s)
切分概率:
p(w|s)=p(w)p(s|w)p(s)
因为始终是同一语句,p(s) 未曾改变, p(s|w) 始终为1. 仅需计算 p(w).
在词表中需记录每个词语的词频,计算每个独立词语出现的联合概率.
使用一元语法(不考虑词语上下文关系)则.
p(wn1)=p(w1,w2,⋯,wn)=p(w1)p(w2)⋯p(wn)=∏n1p(wn)
在实践中一般用对数求和替代求积,原因是词语概率一般会很小,多
次连乘后可能造成溢出.
logp(w)=∑n1logp(wn)
只需要比较大小,所以最后计算结果无需再做一次 log
通过上述公式就可以把“最大”问题化为“最小”问题,“乘积”问题化为
“求和”问题进行求解了。
详例描述:
例如对于输入字符串C"有意见分歧",有S1和S2两种切分可能。
S1:有/ 意见/ 分歧/
S2:有意/ 见/ 分歧/
计算条件概率P(S1|C)和P(S2|C),然后采用概率大的值对应的切分方
其中P(C)是字符串在语料库中出现的概率,只是一个用来归一化的固
定值。从词串恢复到汉字串的概率只有唯一的一种方式,所以
P(C|S)=1。因此,比较P(S1|C)和P(S2|C)的大小变成比较P(S1)和P(S2)
的大小。
①对“有意见分歧”,从左到右进行一遍扫描,得到全部候选词:“有”,
“有意”,“意见”,“见”,“分歧”;
②对每个候选词,记录下它的概率值,并将累计概率赋初值为 0;
③顺次计算各个候选词的累计概率值,同时记录每个候选词的最佳左
邻词;
P’(有) =P(有),
P’(有意) = P(有意) ,
P’(意见) = P’(有) * P(意见) ,(“意见”的最佳左邻词为“有” )
P’(见) = P’(有意) * P(见) , (“见”的最佳左邻词为“有意” )
P’(意见) >P’(见)
“分歧”是尾词,“意见”是“分歧”的最佳左邻词,分词过程结束,输出结
果:有/ 意见/ 分歧/
截图:
总结:
- 主要思想:上下文中,相邻的字同时出现的次数越多,就越可能构成一个词。因此字与字相邻出现的概率或频率能较好的反映词的可信度。2.
- 算法缺点
①最大概率分词法不能解决所有的交集型歧义问题:“这事的确定不下来”:
W1=这/ 事/ 的确/ 定/ 不/ 下来/
W2=这/ 事/ 的/ 确定/ 不/ 下来/
P(W1)
②无法解决组合型歧义问题:“做完作业才能看电视”
W1=做/ 完/ 作业/ 才能/ 看/ 电视/
W2=做/ 完/ 作业/ 才/ 能/ 看/ 电视/