图像铅笔画算法

关于铅笔画算法

---

图像铅笔画算法，属于一直是非真实感绘制领域(Non-Photorealistic Rendering,NPR)中很热门的一个课题，但是计算机也很难模拟出像人一样真实的画质，这也显得CG师们的重要性。本文是基于香港中文大学Cewu Lu等人所做的工作《Combining Sketch and Tone for Pencil Drawing Production》，描述计算机生成铅笔画的艺术。本人才疏学浅，描述如有错误，还望指点。

算法概述

作者基于对日常生活中的人手绘铅笔画的观察，可以分为两个步骤，第一步勾勒出物体的大致轮廓；第二步是对物体进行色调渲染，即用铅笔反复轻轻的划。

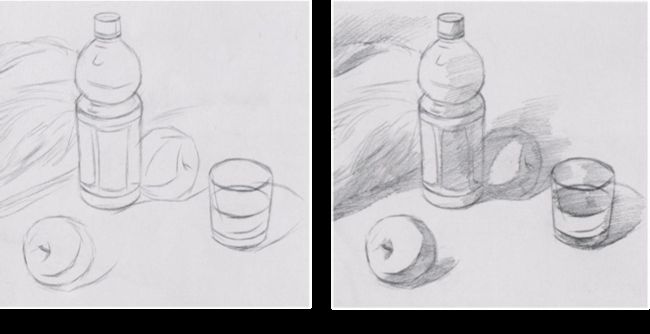
也就是说铅笔画是由结构（Structure）和色调（Tone）组成。

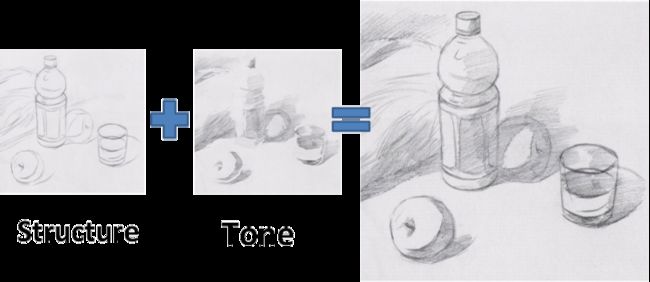
算法步骤如下

1. 产生笔画结构（Stroke Structure Generation ）
2. 色调渲染（Tone Rendering）
3. 笔画结构图与色调渲染图融合得到最终图像

框架图

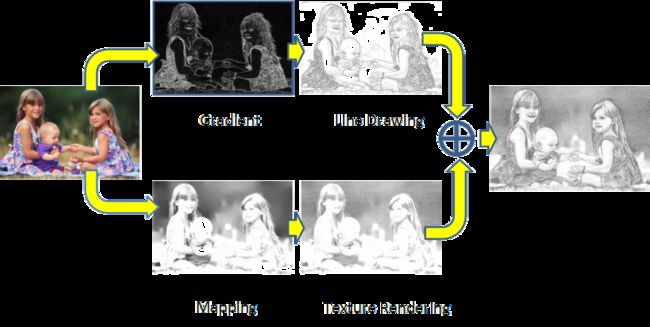
详细步骤

笔画结构的产生

通过对图像求其梯度得到，得到轮廓。

G=((∂ x I) 2 +(∂ y I) 2 ) 12  (1) 

然后检测轮廓中每一点的方向，公式（2），沿着该方向进行扩展（3）。这里，作者是对得到的梯度图G进行8个方向的卷积，响应最大的卷积的方向为视为该点的方向。

C i (p)={G(p)0 ifargmax i {ψ i ⊗G}(p)=iotherwise  (2) 

得到每个点的方向后，再对梯度图进行8个方向的卷积，将8个方向的响应叠加在一起，可得到图像的笔画结构

S=∑ i=1 8 ψ i ⊗C i (3) 

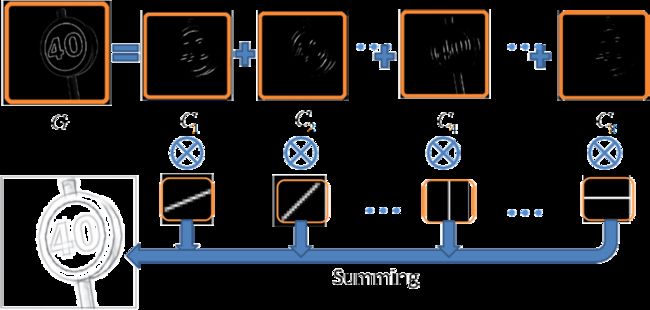
色调渲染

人手绘的铅笔画的直方图往往如下

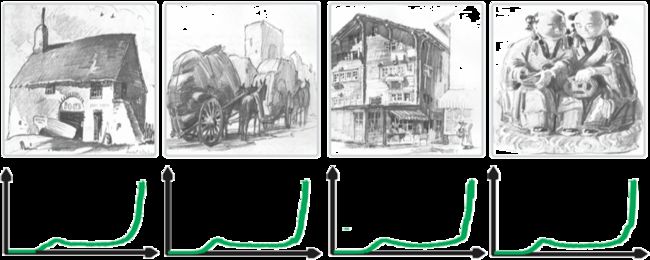
作者解释道，这是因为铅笔画有高光(bright layer)，中间调(mid-tone)，阴影(dark layer)三部分组成，如下图所示。

分别用 拉布拉斯分布，均匀分布，高斯分布函数来模拟。其表达式如下

P 1 (v)=⎧ ⎩ ⎨ 1σ b  e −1−vσ b   0 ifv≤1otherwise  （4） 

P 2 (v)=⎧ ⎩ ⎨ 1u b −u a  0 ifu a ≤v≤u b otherwise  （5） 

P 3 (v)=12πσ d  − − − −  √  e −(v−μ d ) 2 2σ 2 d   （6） 

然后再对这3个函数调节不同的权重，用最大似然估计权重的值。

P(v)=1Z [ω 1 P 1 (v)+ω 2 P 2 (v)+ω 3 P 3 (v)]（7） 

最后一步就是纹理渲染，即模拟人反复用铅笔描的过程。

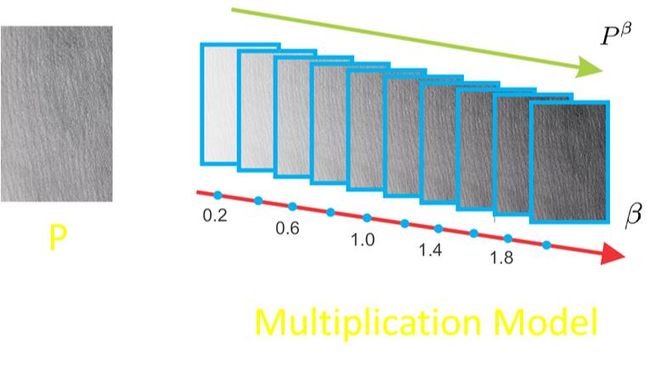
这一步看起来比较抽象，但也简单，就是一个gamma矫正的过程，gamma值越高图像越黑，如图所示。
gamma矫正的示例代码：

I = imread('texture.jpg');
I = rgb2gray(I);
I02 = ((double(I)/255).^0.2);
I04 = ((double(I)/255).^0.4);
I06 = ((double(I)/255).^0.6);
I08 = ((double(I)/255).^0.8);
I12 = ((double(I)/255).^1.2);
I14 = ((double(I)/255).^1.4);
I16 = ((double(I)/255).^1.6);
I18 = ((double(I)/255).^1.8);
I20 = ((double(I)/255).^2.0);

这里未知的就是区域渲染次数 β  ，或者说深度。

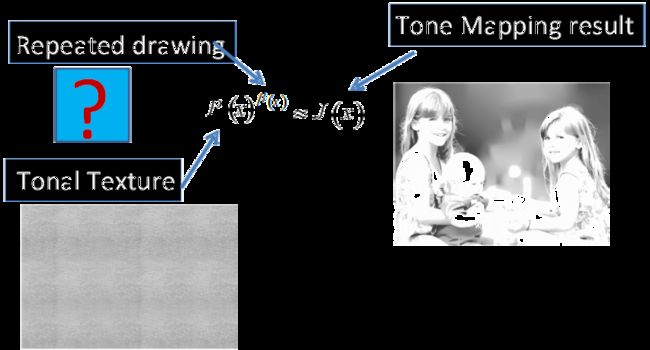
这可以由一个最优化问题解决。

β ∗ =argmin β {∥β∘log(P)−log(J)∥ 2 2 +λ∥∇β∥ 2 2 }（8） 

我们可令 ∥∇β∥ 2 2 =∥D x β∥ 2 2 +∥ ∥ D y β∥ ∥  2 2   ，其中 D x   ， D y   代表水平和竖直方向上的梯度算子，那么该最优化 β  满足下列条件

(β∘log(P)−log(J)) T ∘log(P)+λ(β T D x  T D x +β T D y  T D y )=0 

进一步，两边取转置

(β∘log(P)∘log(P)−log(J)∘log(P))+λ(D x  T D x +D y  T D y )β=0 

由此可解的

[λ(D x  T D x +D y  T D y )+log(P) T log(P)]⋅β=log(P) T log(J) 

转换形式

[diag(log(P)∘log(P))+λ(D x  T D x +D y  T D y )]β=log(J)∘log(P) 

由于 [diag(log(P)∘log(P))+λ(D x  T D x +D y  T D y )]  对称正定，该大规模方程组，可以使用共轭梯度法（CG）求解 β  。

• 纹理图 P
  

• 色调图 J
  

  

• β  图层
  

  

• 纹理渲染图层
  

  
  至此，该算法讲解已算完结了。更多内容可以看原始论文。

代码

• 产生笔画结构代码

function S = GenStroke(im, ks, dirNum)
% ==============================================
%   Compute the Stroke Structure 'S'
%   S = GenStroke(im, ks, dirNum) caculates the direction angle of pixels in  
%  "im", with kernel size "ks", and number of directions "dirNum".
%  
%   Paras:
%   @im        : input image ranging value from 0 to 1.
%   @ks        : kernel size.
%   @dirNum    : number of directions.
%
%           
%   Example
%   ==========
%   im = im2double(imread('npar12_pencil2.bmp'));
%   Iruv = rgb2ycbcr(im);
%   S= GenStroke(Iruv(:,:,1),ks,dirNum);
%   figure, imshow(S)
%
%
%   ==========
%   The code is created based on the method described in
%   "Combining Sketch and Tone for Pencil Drawing Production" Cewu Lu, Li Xu, Jiaya Jia 
%   International Symposium on Non-Photorealistic Animation and Rendering (NPAR 2012), June, 2012

%  image gradients
    [H, W, sc] = size(im);
    if sc == 3
        im = rgb2gray(im);
    end
    imX = [abs(im(:,1:(end-1)) - im(:,2:end)),zeros(H,1)];
    imY = [abs(im(1:(end-1),:) - im(2:end,:));zeros(1,W)];  
    imEdge = imX + imY;

% convolution kernel with horizontal direction 
    kerRef = zeros(ks*2+1);
    kerRef(ks+1,:) = 1;

% classification 
    response = zeros(H,W,dirNum);
    for n = 1 : dirNum
        ker = imrotate(kerRef, (n-1)*180/dirNum, 'bilinear', 'crop');
        response(:,:,n) = conv2(imEdge, ker, 'same');
    end

    [~ , index] = max(response,[], 3); 

 % create the sketch
    C = zeros(H, W, dirNum);
    for n=1:dirNum
        C(:,:,n) = imEdge .* (index == n);
    end

    Spn = zeros(H, W, dirNum);
    for n=1:dirNum
        ker = imrotate(kerRef, (n-1)*180/dirNum, 'bilinear', 'crop');
        Spn(:,:,n) = conv2(C(:,:,n), ker, 'same');
    end

    Sp = sum(Spn, 3);
    Sp = (Sp - min(Sp(:))) / (max(Sp(:)) - min(Sp(:)));
    S = 1 - Sp;

• 纹理传输代码

 function T = texturetransfer(P,J)
 % ==============================================
%   Texture Rendering
%   T = texturetransfer(P,J) pencil texture transfer from P to 
J 
%  
%   Paras:
%   @P        : tonal texture value from 0 to 1.
%   @J        : pencil tone image value for 0 to 1. 
%
%           
%   Example
%   ==========
%   P = im2double(rgb2gray(imread('TonalTexture.jpg')));
%   J = im2double(rgb2gray(imread('PencilTone.jpg'))); 
%   T = texturetransfer(P,J);
%   figure,imshow(T); title('T');


lambda =0.2;

[r,c,~] = size(P);
k = r*c;

% Transform to log domain
logP = log(P + eps);
logP = logP(:);
logJ = log(J + eps);
logJ = logJ(:);

dx = ones(k,1);
dx = dx(:);

dy = ones(k,1);
dy = dy(:);

B(:,1) = dx;
B(:,2) = dy;
d = [-r,-1];
A = spdiags(B,d,k,k);

e = padarray(dx, r,'post'); e = e(r+1:end);
w = padarray(dx, r,'pre');  w = w(1:end-r);
s = padarray(dy, 1,'post'); s = s(2:end);
n = padarray(dy, 1,'pre');  n = n(1:end-1);

D = -(e+w+s+n);
A = lambda*(A + A' + spdiags(D,0,k,k)) + spdiags(logP.*logP,0,k,k);
b = logJ.*logP;

%Solve 
beta = pcg(A,b,1e-6,60);
beta = reshape(beta,r,c);
beta = (beta - min(beta(:))) / (max(beta(:)) - min(beta(:))) * 4;
figure,imshow(beta./max(beta(:)));
T = (P).^beta;

注: 这里我给出的只是第一步产生笔画结构的代码，和纹理渲染部分代码，只有色调映射部分未给。若对此算法感兴趣，可以参考作者论文。另外作者主页上有部分代码，可以下载

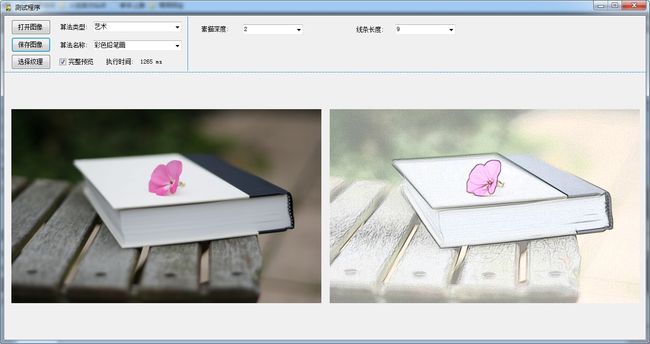
效果

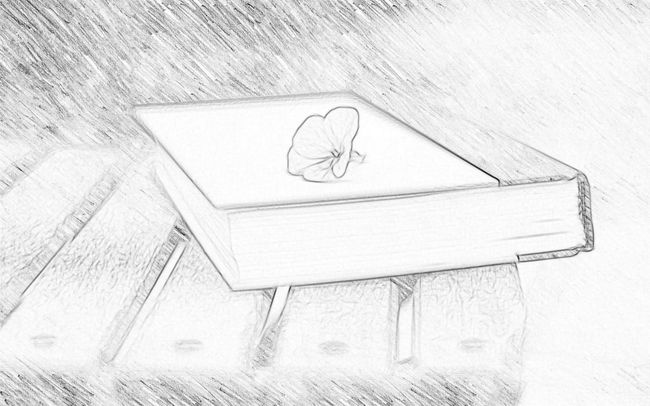
图片来源互联网，侵权则删。

致谢

在此感谢采石工（QQ544617183）指正公式求解过程中几处不正确。
附上采石工的推导证明

软件下载地址（可执行程序exe）

感兴趣的朋友可以点此下载，尝试效果。

更多阅读

http://www.cnblogs.com/Imageshop/p/4285566.html
http://www.cse.cuhk.edu.hk/~leojia/projects/pencilsketch/pencil_drawing.htm

转载请保留以下信息

作者	日期	联系方式
风吹夏天	2015年5月2日	wincoder#qq.com