folly SparseByteSet详解

Folly SparseByteSet详解

缘起

       如果对stl的bitset有所了解的话，那么SparseByteSet是比bitset的性能更强的一个替代物。这里首先简要回顾一下bitset的功能。bitset可以认为是一个bool的静态数组，stl也有一个bool的动态数组版本，即元素类型特化为bool的vector，他们都用一个bit来存储每个bool类型，这样子1个byte的空间可以存储8个bool类型，从而大大提升空间效率。但是，bitset想C/C++的原生数组一样，空间是在初始化的时候预先分配好的，不能在后续动态扩展。

      SparseByteSet和bitset一样也是一个静态的bool数组。但是它针对特殊场景，进行了性能优化，首先程序对空间不敏感；其次程序应用的场景只有插入和查询操作，没有更新和删除操作；再次主要在栈上使用这个bool数组。那么为什么叫SparseByteSet呢，Sparse是“稀疏的”意思，透露出它是用稀疏byte数组的方式来存储bool值。

      针对上面描述的两个场景，SparseByteSet设计得是如此简单，简单到除了构造函数，只有两个方法，add和contains，没有任何多余的地方，非常轻量级。

 

原理分析

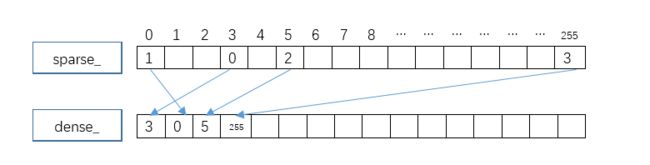
     SparseByteSet包含三个成员变量，size_, sparse_, dense_。size_用来保存当前保存了多少个值为true的bool值；sparse_是一个256byte的数组，其自身的每个元素的索引位置表示我们保存的值为true的bool值的索引位置，其对应的元素值则作为指向dense_中的元素位置的索引，它保存的值可以是不连续的，也就是说它是稀疏数组；dense_也是一个256byte的数组，SparseByteSet中保存的元素在这里是连续存储的，size_之外的元素不管是什么值都是为空的，也就是说这个是稠密数组。

    上图是依次设置了序号为0、3、5、255 之后的SparseByteSet中的内存状态。

 

     现在来推演一下contains的实现原理，即给定元素的位置，要判断这个元素是否被设置为true了：

     假设输入的这个元素位置为idx，那么首先从sparse_中获取索引位置为idx元素的值，譬如，idx=5，那么上图中sparse_[5] = 2。

     然后根据获取的sparse_[idx]和size_进行比较，如果前者大于等于size_，那么这个idx对应的元素肯定是没有被添加进来的；如果前者小于size_，那么要比较以sparse_[idx]为索引的dense_中的元素的值是否为idx来进一步确认是否这个idx对应的元素是被真正添加进来的元素。至此就完成了整个contains的过程。

 

    下面再来推荐add的实现原理：

    假设要添加一个idx为6的值为true 的bool元素。

    首先，需要通过contains来判断这个idx的元素是否已经存在了，如果已经存在了，则直接返回添加成功。

    如果元素不存在，那么将sparse_[idx]设置为size_（因为size_为索引的dense_位置最靠前的一个空位），也就是说在dense_上分配一个新的元素位置。

     然后将dense_[size_]设置为idx。

     最后将size_ 加 1。

 

 

      添加idx为6的值为true的bool元素完成后的内存状态如下：

 

疑问

为什么要如此费劲地创建sparse_和dense_两个数组，不是一个数组就可以完成所需要的功能了么？

答：    没错，但是前提条件是在构造SparseByteSet的时候要对存储bool元素的数组进行初始化。如果元素没有初始化，仅仅靠一个数组是无法完成既要实现O(1)复杂度的插入，又要在实现O(1)复杂度的查找的。

       如前所述，SparseByteSet的应用场景是用在短平快的栈空间里面的，通过代码可以看到，它的构造函数只是初始化了size_变量，对于sparse_和dense_两个数组是没有进行初始化的。对于短平快的应用场景，几百字节的memset的CPU消耗其实是非常客观的。

       但是不进行数组的初始化，那么必然带来这两个数组的值是不确定的副作用，不能假设这两个数组中的所有元素初始化值为0了，或者任何其他值。

       同样，SparseByteSet在析构的时候也很方便，没有任何需要额外回收处理的东西，函数直接从栈里面返回（CPU通过调整栈指针）就直接把空间回收了。可以说确实是名副其实的短平快。

      而sparse_和dense_两个数组的设计安排，加上size_变量，就解决了元素值未初始化带来的不确定性问题。

     当SparseByteSet为空的时候，来分析一下contains函数的判断过程：

     sparse_[idx]可以为任意值，假设为n， 那么n必然>=size，所以返回未找到。

     当SparseByteSet不为空的时候，来分析一下containes函数的判断过程：

     假设idx这个元素没有保存，那么sparse_[idx]可以为任意值，假设为n，当然如果n>=size_，那么显然可以返回未找到；如果这个任意值n

     这样子，SparseByteSet就完美解决了数组未初始化带来的不确定性问题。

 

为什么用byte保存一个bool值，而不像bitset一样按bit存储的一个byte里面，这样子不是让费空间么？

答： 其实，这个主要还是基于性能的考虑。要定位到一个byte中的某个bit，然后判断某个bit是否被置为了，至少包含以下几个步骤：

1. 根据索引位置整除8，定位到应该从那个byte取值；
2. 根据所有位置取8的模，得到byte中的bit位置；
3. 根据bit的位置，获取对应的掩码；
4. 根据掩码，和这个byte进行与操作，如果不等于0，则对应位置值为true，否则为0。

而SparseByteSet则简单得多很多了。只要进行两次访存操作加上两次判断就可以了，非常简单。以代码为证：

  inline bool contains(uint8_t i) const {

    return sparse_[i] < size_ && dense_[sparse_[i]] == i;

  }