【Keras】DNN神经网络模型

DNN(Deep Neural Network)神经网络模型又叫全连接神经网络，是基本的深度学习框架。与RNN循环神经网络、CNN卷积神经网络的区别就是DNN特指全连接的神经元结构，并不包含卷积单元或是时间上的关联。

1、梳理一下DNN的发展历程

神经网络技术起源于上世纪五、六十年代，当时叫感知机（perceptron），拥有输入层、输出层和一个隐含层。输入的特征向量通过隐含层变换达到输出层，在输出层得到分类结果。但是，Rosenblatt的单层感知机有一个严重得不能再严重的问题，即它对稍复杂一些的函数都无能为力（比如最为典型的“异或”操作）。

计算公式：

常见响应函数(非线性函数)
logistic/sigmoid function：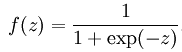
tanh function：
step/binary function：
rectifier function：
analytic function：rectifier function的平滑近似：

随着数学的发展，这个缺点直到上世纪八十年代才被Rumelhart、Williams、Hinton、LeCun等人发明的多层感知机（multilayer perceptron）克服。多层感知机，顾名思义，就是有多个隐含层的感知机。

图：上下层神经元全部相连的神经网络——多层感知机

多层感知机可以摆脱早期离散传输函数的束缚，使用sigmoid或tanh等连续函数模拟神经元对激励的响应，在训练算法上则使用Werbos发明的反向传播BP算法，这就是我们现在所说的神经网络NN。多层感知机解决了之前无法模拟异或逻辑的缺陷，同时更多的层数也让网络更能够刻画现实世界中的复杂情形。多层感知机给我们带来的启示是，神经网络的层数直接决定了它对现实的刻画能力——利用每层更少的神经元拟合更加复杂的函数。但是随着神经网络层数的加深，优化函数越来越容易陷入局部最优解，并且这个“陷阱”越来越偏离真正的全局最优。利用有限数据训练的深层网络，性能还不如较浅层网络。同时，另一个不可忽略的问题是随着网络层数增加，“梯度消失”现象更加严重。具体来说，我们常常使用sigmoid作为神经元的输入输出函数。对于幅度为1的信号，在BP反向传播梯度时，每传递一层，梯度衰减为原来的0.25。层数一多，梯度指数衰减后低层基本上接受不到有效的训练信号。

2006年，Hinton利用预训练方法缓解了局部最优解问题，将隐含层推动到了7层，神经网络真正意义上有了“深度”，由此揭开了深度学习的热潮。这里的“深度”并没有固定的定义——在语音识别中4层网络就能够被认为是“较深的”，而在图像识别中20层以上的网络屡见不鲜。为了克服梯度消失，ReLU、maxout等传输函数代替了sigmoid，形成了如今DNN的基本形式。单从结构上来说，全连接的DNN和图1的多层感知机是没有任何区别的。

DNN在使用过程中也存在一些弱点，全连接DNN的结构里下层神经元和所有上层神经元都能够形成连接，带来的潜在问题是参数数量的膨胀。假设输入的是一幅像素为1K*1K的图像，隐含层有1M个节点，光这一层就有10^12个权重需要训练，这不仅容易过拟合，而且极容易陷入局部最优。另外，图像中有固有的局部模式（比如轮廓、边界，人的眼睛、鼻子、嘴等）可以利用，显然应该将图像处理中的概念和神经网络技术相结合。

2、进一步梳理DNN的构造进行理解

首先是神经元的运算逻辑，一定是线性内核和非线性激活相结合，所以神经元的算法是非线性的。因此DNN神经元的计算内核为X*W+b，以softmax函数（二元分类中使用Sigmoid函数）为非线性核的构造方式。同理，RNN的核采用RNN运算内核，CNN采用卷积运算内核。

逻辑分类可以视为一层DNN神经网络，计算内核为X*W+b，以softmax函数（二元分类中使用Sigmoid函数）为非线性核的构造方式。像逻辑分类这种，线性运算单元设计为权重相乘的，并且层与层之间的神经元全部相连的神经网络就是全连接神经网络，即DNN。

进一步增加隐层，，容纳更多的神经元，来增强模型的能力。比起浅层模型在特征工程和模型工程的各种尝试，神经网络通过更多的神经元直接增强模型的能力。

#由于不能链接到官方的已经处理好的数据，所以这里通过tensorflow导入mnist数据
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
#from _future_ import print_function
import numpy as np
#from keras.dataseets import mnist
from keras.models import Sequential
from keras.layers import Dense
from keras.utils import np_utils

batch_size = 128 #梯度下降一个批（batch）的数据量
nb_classes =10 #类别
nb_epoch =10 #梯度下降epoch循环训练次数，每次循环包含全部的样本
image_size = 28*28 #输入图片的大小，由于是灰度图片，因此只有一个颜色通道

#加载数据
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
x_train,y_train= mnist.train.images, mnist.train.labels
#print(x_train.shape,y_train.shape) #(55000, 784) (55000, 10)
x_test,y_test= mnist.test.images, mnist.test.labels
#print(x_test.shape,y_test.shape) #(10000, 784) (10000, 10)
#如果y_train\y_test不是one_hot编码，需要进行转换
'''
#例如将[2,3,...]编码成[[0,0,1,,,],[0,0,0,1,,,]]
#导入编码模块
from keras.utils import np_utils
y_train  = np_utils.to_categorical(y_train,nb_classes)
y_test = np_utils.to_categorical(y_test,nb_classes)
'''
#创建模型，逻辑分类相当于一层全链接的神经网络（Dense是Keras中定义的DNN模型）
model = Sequential([Dense(128,input_shape=(image_size,),activation= 'relu'),Dense(10,input_shape=(128,),activation= 'softmax')])

model.compile(optimizer = 'rmsprop',loss = 'categorical_crossentropy',metrics= ['accuracy'])
model.fit(x_train,y_train,batch_size = batch_size,nb_epoch = nb_epoch,verbose = 1,validation_data = (x_test,y_test))
#score分数包含两部分，一部分是val_loss,一部分是val_acc。取score[1]来进行模型的得分评价
score = model.evaluate(x_test,y_test,verbose = 0)
print('Accuracy:{}'.format(score[1]))

注意，这里添加的隐层中，激活函数是activation= ‘relu’,ReLu函数是一个非线性函数，如图：

这个模型对比Sigmoid系主要变化有三点：①单侧抑制 ②相对宽阔的兴奋边界 ③稀疏激活性（重点，可以看到红框里前端状态完全没有激活）

同年，Charles Dugas等人在做正数回归预测论文中偶然使用了Softplus函数，Softplus函数是Logistic-Sigmoid函数原函数：Softplus(x)=log(1+ex)。按照论文的说法，一开始想要使用一个指数函数（天然正数）作为激活函数来回归，但是到后期梯度实在太大，难以训练，于是加了一个log来减缓上升趋势。加了1是为了保证非负性。同年，Charles Dugas等人在NIPS会议论文中又调侃了一句，Softplus可以看作是强制非负校正函数max(0,x)平滑版本。偶然的是，同是2001年，ML领域的Softplus/Rectifier激活函数与神经科学领域的提出脑神经元激活频率函数有神似的地方，这促成了新的激活函数的研究。

**整个含隐层的DNN的算法流程就是：
X ——W1*X1+b1 ——Relu——W2*X2+b2 ——softmax——y**

值得注意的是，如果选择ReLu激活函数的话，调参数时需要注意设定的学习速率，不要让过多的神经元处于ReLu函数左边额死亡状态。