SVM算法学习

SVM算法原理

SVM算法是专门用来处理线性不可分的分类问题的，当然它也可以用来处理回归问题。它用来处理这类问题的方式一般是将数据投射到更高维的空间中，其中用得最普遍的两种升维方法分别是多项式内核(Polynomial kernel)和径向基内核(RBF)。

SVM的核函数区别

下面用一个酒的分类来说明几个核函数之间的区别：

from sklearn.datasets import load_wine
from sklearn import svm
import matplotlib.pyplot as plt
import numpy as np
#画图函数
def make_meshgrid(x,y,h=.02):
    x_min,x_max = x.min()-1,x.max()+1
    y_min,y_max = y.min()-1,y.max()+1
    xx,yy = np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h))
    return xx,yy
#绘制等高线
def plot_contours(ax,clf,xx,yy,**params):
    Z = clf.predict(np.c_[xx.ravel(),yy.ravel()])
    Z = Z.reshape(xx.shape)
    out = ax.contourf(xx,yy,Z,**params)
    return out
#使用酒数据集
wine = load_wine()
#选取数据集的前两个特征
X = wine.data[:,:2]
y = wine.target

C = 1.0 #正则化参数
models = (svm.SVC(kernel='linear',C=C),
         svm.LinearSVC(C=C),
         svm.SVC(kernel='rbf',gamma=0.7,C=C),
         svm.SVC(kernel='poly',degree=3,C=C))
models = (clf.fit(X,y) for clf in models)
#设置图题
titles = ('SVC with linear kernel',
         'LinearSVC (linear kernel)',
         'SVC with RBF kernel',
         'SVC with polynomial (degree 3) kernel')
#设定子图形
fig,sub = plt.subplots(2,2)
plt.subplots_adjust(wspace=0.4,hspace=0.4)
#作图
X0,X1 = X[:,0],X[:,1]
xx,yy = make_meshgrid(X0,X1)
for clf,title,ax in zip(models,titles,sub.flatten()):
    plot_contours(ax,clf,xx,yy,cmap=plt.cm.plasma,alpha=0.8)
    ax.scatter(X0,X1,c=y,cmap=plt.cm.plasma,s=20,edgecolor='k')
    ax.set_xlim(xx.min(),xx.max())
    ax.set_ylim(yy.min(),yy.max())
    ax.set_xlabel('Feature 0')
    ax.set_ylabel('Feature 1')
    ax.set_xticks(())
    ax.set_yticks(())
    ax.set_title(title)
plt.show()

运行结果如下：

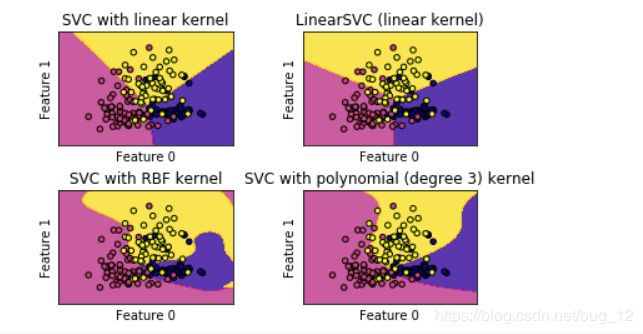
从图中我们可以看到线性内核的SVC与linearSVC得到的结果非常近似，只有一点点差别，这个差别在于L2，L1范数上。它们的决定边界都是线性的，在更高维上自然就是想交的超平面。而RBF内核的SVC和Polynomial内核的SVC分类器的决定边界则不是线性的，是弹性的。其中起决定性作用的是gamma,C和degree。

SVM回归分析-波士顿房价

SVM同样可以用于回归分析，下面用一个例子来说明：
首先在进行房价回归分析之前，我们首先要选择核函数。

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.svm import SVR
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
boston = load_boston()
scaler = StandardScaler()
#划分训练集、测试集
X,y = boston.data,boston.target
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.2,random_state=8)
#预处理
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)

#分别测试Linear,rbf看谁表现好
for kernel in ['linear','rbf']:
    svr = SVR(kernel=kernel)
    svr.fit(X_train_scaled,y_train)
    print(kernel,'核函数模型训练集得分: {:.2f}'.format(svr.score(X_train_scaled,y_train)))
    print(kernel,'核函数模型测试集得分: {:.2f}'.format(svr.score(X_test_scaled,y_test)))

运行结果如下：

但是由于RBF还可以通过调整C和gamma两个参数来提高模型得分，所以最后我们选择的核函数是RBF。下面通过调整C和gamma来得到较高的模型得分。

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.svm import SVR
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
boston = load_boston()
scaler = StandardScaler()
#划分训练集、测试集
X,y = boston.data,boston.target
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.2,random_state=8)
#预处理
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
#训练模型
svr = SVR(kernel='rbf',C=60,gamma=0.2)
svr.fit(X_train_scaled,y_train)
print(kernel,'核函数模型训练集得分: {:.2f}'.format(svr.score(X_train_scaled,y_train)))
print(kernel,'核函数模型测试集得分: {:.2f}'.format(svr.score(X_test_scaled,y_test)))

运行结果如下：

这是一个相当不错的结果了，通过C和gamma两个参数的调节，rbf的训练集得分和测试集得分都在百分之90以上。

总结

SVM算法是一个相当强大的算法，对于各种不同类型的数据集都有不错的效果。在应对低维和高维的数据集上表现都很不错。但是在样本数量巨大时，SVM算法就会十分耗费内存和时间。并且SVM对于数据预处理和参数调节的要求十分的高，这也算是它的缺点之一。但是，总的来说，SVM算法还是相当强大的。