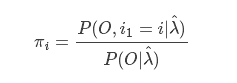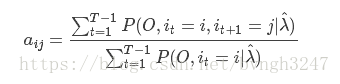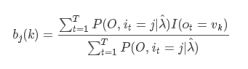语音识别算法原理文档整理(五)
HMM算法
隐马尔可夫模型的参数一般称为其三要素,包括初始状态概率,转移概率和观测概率。
三个主流算法:
概率计算问题即模型评价问题——前向算法和后向算法
学习问题即参数估计问题——Baum-Welch算法
预测问题即解码问题——Viterbi算法
前向算法与后向算法
首先引入前向变量αt(i):在时间t时刻,HMM输出序列为O1O2…OT,在第t时刻位于状态si的概率。

前向算法
step1 初始化:α1(i) = πi*bi(O1), 1≤i≤N
step2 归纳计算:
![]()
step3 终结:
P(O|μ)= ![]()
先介绍后向变量βt(i):给定模型μ=(A,B,π),并且在时刻t,状态为si的前提下,输出序列为Ot+1Ot+2…OT的概率,即
后向算法
step1 初始化:βt (i)=1, 1≤i≤N
step2 归纳计算:

1≤t≤T-1, 1≤i≤Ns
step3 求终结和:
P(O|μ)= 
参考网址:http://www.cnblogs.com/sjjsxl/p/6285629.html
Baum-Welch算法
Baum-Welch算法就是EM算法在隐马尔科夫模型学习中的具体体现。
隐马尔可夫模型事实上是一个含有隐变量的概率模型
P(O|λ)=∑IP(O|I,λ)P(I|λ)
1.确定完全数据的对数似然函数
所有观测数据写成O=(o1,o2,…,oT),所有隐数据写成I=(i1,i2,…,iT),完全数据是(O,I)=(o1,o2,…,oT,i1,i2,…,iT)。完全数据的对数似然函数是logP(O,I|λ)。
2.EM算法的E步:求Q函数Q(λ,λ^)
![]()
函数Q(λ,λ^)可以写成:
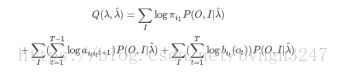
3.EM算法的M步:极大化Q函数Q(λ,λ^)求模型参数A,B,π ,求导得
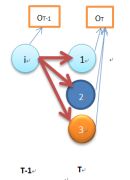
物体意义解释如下图所示:
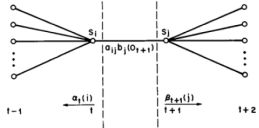
在给定模型λ和观测O,在时刻t处于状态qi且在时刻t+1处于状态qj的概率。aij分子上的式子我们给出了具体的求解公式,除了t和t+1时刻,累加其他所有时刻的隐含状态(节点),主要原因在于对节点图的计算就是对∑IP(O,I|λ^)的计算过程。
参考网址:http://blog.csdn.net/u014688145/article/details/53046765?locationNum=7&fps=1