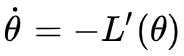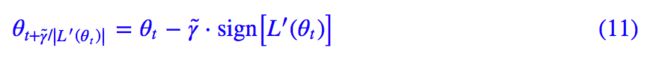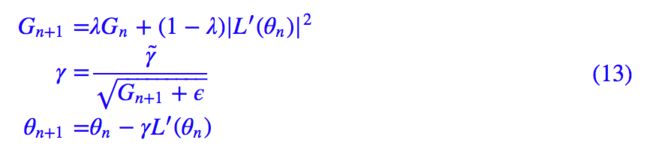从动力学角度看优化算法：自适应学习率算法

作者丨苏剑林

单位丨广州火焰信息科技有限公司

研究方向丨NLP，神经网络

个人主页丨kexue.fm

在从动力学角度看优化算法SGD：一些小启示一文中，我们提出 SGD 优化算法跟常微分方程（ODE）的数值解法其实是对应的，由此还可以很自然地分析 SGD 算法的收敛性质、动量加速的原理等等内容。

在这篇文章中，我们继续沿着这个思路，去理解优化算法中的自适应学习率算法。

RMSprop

首先，我们看一个非常经典的自适应学习率优化算法：RMSprop。RMSprop 虽然不是最早提出的自适应学习率的优化算法，但是它却是相当实用的一种，它是诸如 Adam 这样更综合的算法的基石，通过它我们可以观察自适应学习率的优化算法是怎么做的。

算法概览

一般的梯度下降是这样的：

很明显，这里的 γ 是一个超参数，便是学习率，它可能需要在不同阶段做不同的调整。而 RMSprop 则是：

算法分析

对比朴素的 SGD，可以发现 RMSprop 在对 θ 的更新中，将原来是标量的学习率 γ，换成了一个向量。

如果把这个向量也看成是学习率，那么 RMSprop 就是找到了一个方案，能够给参数的每个分量分配不同的学习率。

这个学习率的调节，是通过因子来实现的，而则是梯度平方的滑动平均。本质上来说，“滑动平均”平均只是让训练过程更加平稳一些，它不是起到调节作用的原因，起作用的主要部分是“梯度”，也就是说，可以用梯度大小来调节学习率。

自适应学习率

为什么用梯度大小可以来调节学习率呢？其实这个思想非常朴素。

极小值点和ODE

话不多说，简单起见，我们先从一个一维例子出发：假设我们要求 L(θ) 的一个极小值点，那么我们引入一个虚拟的时间参数 t，转化为 ODE：

不难判断，L(θ) 的一个极小值点就是这个方程的稳定的不动点，我们从任意的 θ0 出发，数值求解这个 ODE，可以期望它最终会收敛于这个不动点，从而也就得到了一个极小值点。

最简单的欧拉解法，就是用去近似，从而得到：

也就是：

这就是梯度下降法了，θt+γ 相当于 θn+1，而 θt 相当于 θn，也就是每步前进 γ 那么多。

变学习率思想

问题是，γ 选多少为好呢？当然，从“用去近似”这个角度来看，当然是 γ 越小越精确，但是 γ 越小，需要的迭代次数就越多，也就是说计算量就越大，所以越小越好是很理想，但是不现实。

所以，最恰当的方案是：每一步够用就好。可是我们怎么知道够用了没有？

因为我们是用去近似的，那么就必须分析近似程度：根据泰勒级数，我们有：

在我们这里有，那么我们有：

可以期望，当 γ 比较小的时候，误差项，也就是说，在一定条件下，γ∣L′(θt)∣ 本身就是误差项的度量，如果我们将 γ∣L′(θt)∣  控制在一定的范围内，那么误差也被控制住了。即：

其中 γ̃ 是一个常数，甚至只需要简单地 γ∣L′(θt)∣=γ̃（暂时忽略 L′(θt)=0 的可能性，先观察整体的核心思想），也就是：

这样我们就通过梯度来调节了学习率。

滑动平均处理

读者可能会诟病，把 γ=γ̃/∣L′(θt)∣ 代入原来的迭代结果，不就是：

整个梯度你只用了它的符号信息，这是不是太浪费了？过于平凡：也就是不管梯度大小如何，每次迭代 θ 都只是移动固定的长度。

注意，从解 ODE 的角度看，其实这并没有毛病，因为 ODE 的解是一条轨迹 (t,θ(t))，上面这样处理，虽然 θ 变得平凡了，但是 t 却变得不平凡了，也就是相当于 t,θ 的地位交换了，因此还是合理的。

只不过，如果关心的是优化问题，也就是求 L(θ) 的极小值点的话，那么上式确实有点平凡了，因为如果每次迭代 θ 都只是移动固定的长度，那就有点像网格搜索了，太低效。

所以，为了改善这种不平凡的情况，又为了保留用梯度调节学习率的特征，我们可以把梯度平均一下，结果就是：

这个 λ 是一个接近于 1 但是小于 1 的常数，这样的话 Gt 在一定范围内就比较稳定，同时在一定程度上保留了梯度 L′(θt) 本身的特性，所以用它来调节学习率算是一个比较“机智”的做法。为了避免 t+γ̃,t+γ 引起记号上的不适应，统一用 n,n+1 来表示下标，得到：

这就是开头说的 RMSprop 算法了。

高维情形分析

上面的讨论都是一维的情况，如果是多维情况，那怎么推广呢？ 

也许读者觉得很简单：把标量换成向量不就行了么？并没有这么简单，因为 (13) 推广到高维，至少有两种合理的选择：

或：

前者用梯度的总模长来累积，最终保持了学习率的标量性；后者将梯度的每个分量分别累积，这种情况下调节后的学习率就变成了一个向量，相当于给每个参数都分配不同的学习率。要是从严格理论分析的角度来，其实第一种做法更加严密，但是从实验效果来看，却是第二种更为有效。

我们平时所说的 RMSprop 算法，都是指后者 (15)。但是有很多喜欢纯 SGD 炼丹的朋友会诟病这种向量化的学习率实际上改变了梯度的方向，导致梯度不准，最终效果不够好。所以不喜欢向量化学习率的读者，不妨试验一下前者。

结论汇总

本文再次从 ODE 的角度分析了优化算法，这次是从误差控制的角度给出了一种自适应学习率算法（RMSprop）的理解。至于我们更常用的 Adam，则是 RMSprop 与动量加速的结合，这里就不赘述了。

将优化问题视为一个常微分方程的求解问题，这其实就是将优化问题变成了一个动力学问题，这样可以让我们从比较物理的视角去理解优化算法（哪怕只是直观而不严密的理解），甚至可以把一些 ODE 的理论结果拿过来用，后面笔者会试图再举一些这样的例子。

点击以下标题查看作者其他文章： 

• 变分自编码器VAE：原来是这么一回事 | 附开源代码

• 再谈变分自编码器VAE：从贝叶斯观点出发

• 变分自编码器VAE：这样做为什么能成？

• 从变分编码、信息瓶颈到正态分布：论遗忘的重要性
  

• 深度学习中的互信息：无监督提取特征

• 全新视角：用变分推断统一理解生成模型

• 细水长flow之NICE：流模型的基本概念与实现

• 细水长flow之f-VAEs：Glow与VAEs的联姻

• 深度学习中的Lipschitz约束：泛化与生成模型
  

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？ 答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

投稿邮箱：

• 投稿邮箱：[email protected] 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。

▽ 点击 | 阅读原文 | 查看作者博客