评估图像质量评价算法性能的几个常用的标准

The ‘good-ness’ of any algorithm is gauged by measuring the correlation of algorithmic scores with subjective (differential) mean opinion scores (DMOS/MOS) on a large dataset spanning different distortion.

正如以上所说对于一种图像质量评价算法性能好坏的评估就是看在具有不同失真的大数据集上观察者的主观评分和算法评分的相关度。如果它们的相关度较高，则说明该质量评价算法的性能较好，否则反之。

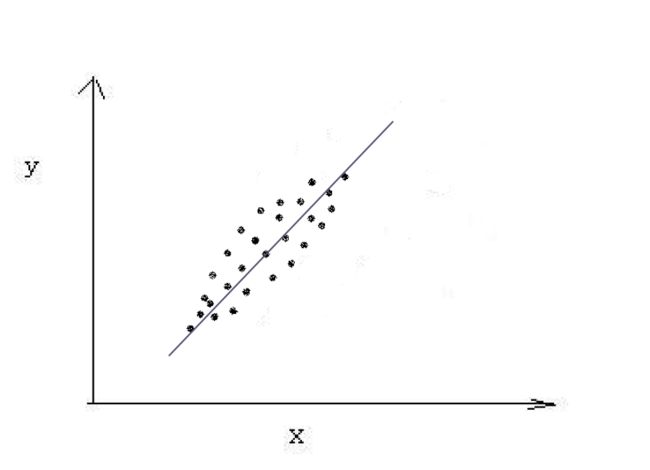
那么什么是相关呢？简单的说就是当一个或几个相互联系的变量取一定数值时，与之相对应的另一个变量的值虽然不确定，但它仍然按某种规律在一定范围内变化，变量间的这种关系，被称为相关关系。相关关系可以用相关系数来评价，其绝对值越高表明其越相关，否则反之。相关系数的取值一般在-1到1之间。可以回想一下我们学过的概率论与数理统计中的相关系数，当两个随机变量的相关系数的绝对值为1时，可以将一个随机变量表示为另一个随机变量的一元线性函数，这时变量的相关度最高。例如Y=a*X+b。但是当其相关系数的绝对值小于1时，就不会有这么明确的函数关系。此时的相关度较小。下图是两个变量相关的示例，图中的每一点是变量X，Y的一对取值。可以看出这两个变量近似于线性相关，其相关系数接近于1。

现在用到的评价参数主要有四个。它们分别是SROCC,KROCC,PLCC和rMSE。下面分别对它们进行具体介绍。因为现在由于做图像质量评价的需要，我只是大概了解一下它们所表达的含义以及它们的计算方法，可能不像统计学中那么的专业。

1. SROCC

SROCC的全称是the Spearman rank-order correlation coefficient，又简称为Spearman’s rho。下面我先例举一个具体的例子，然后对其进行具体介绍。

假设现在有10个学生的数学(X)和英语(Y)成绩，现在我们要来判断X和Y的相关性。

num	X	Y	Rank(X)	Rank(Y)	d	d2
1	56	66	9	4	5	25
2	75	70	3	2	1	1
3	45	40	10	10	0	0
4	71	60	4	7	-3	9
5	62	65	6	5	1	1
6	64	56	5	9	-4	16
7	58	59	8	8	0	0
8	80	77	1	1	0	0
9	76	67	2	3	-1	1
10	61	63	7	6	1	1

如上表所示，X列表示某个学生的数学成绩，Y列表示其对应的英语成绩。然后分别对数学成绩和英语成绩进行等级划分，分数最高的划分为1，最低的划分为10，其它的以此分别划分为2到9之间的一个整数。划分后如Rank(X)列和Rank(Y)列所示。然后对得到的每一个同学的数学成绩等级减去英语成绩等级得到数据列d，然后对d平方得到d的平方数据列。在这个过程中如果某几个同学的某一门成绩相同，例如张三和李四的数学成绩都是70，假设它们被划分的等级分别为3和4，反之亦然，则需要先对等级划分进行平均，这里等级平均后是3.5，然后把它们的等级划分都定为3.5。下面我们就可以来计算它们的SROCC了。

公式一：

srocc=1−6∑ni=1d2in(n2−1)

公式二：

srocc=∑ni=1(ui−u¯)(vi−v¯)∑ni=1(ui−u¯)2∑ni=1(vi−v¯)−−−−−−−−−−−−−−−−−−−−−−√

对于以上两个公式，当某个特定的数据集合(如数学成绩)中有相等的值时使用公式二，否则使用公式一。其中n为采集的数据样本中数据对的个数，上例中n为10。其中 u¯ 和 v¯ 分别为某个特定的数据集合在完成等级划分之后的等级平均值，比如上例中数学成绩的等级平均。 ui 和 vi 分别对相应数据对的等级划分。

我们从以上例子可以看出srocc主要评价的是两组数据的等级相关性。也就是对于两个变量的一些数据对(如上例所示)，数据对的意思是当一个变量取一个值时观察到另一个变量取到的值，当对每个变量的数据进行等级划分后，我们可以得到每个变量的等级序列，如上例中的Rank(X)和Rank(Y),若两个变量的srocc越高则表明它们的等级相关性较高(比如对于上例中任意的i，若 Rank(xi) = Rank(yi) ,则表明它们的等级相关非常高，srocc=1)，否则反之。

2.KROCC

KROCC的全称是the Kendall rank-order correlation coefficient，又简称为Kendall’s tau。和srocc一样这里我也是通过例子计算来解释它。在这里我还是用srocc中的那个例子。

在这里我先讲一些基本的概念。假设我们现在需要评价两个变量X和Y的相关性， (x1,y1) , (x2,y2) ,……., (xn,yn) 是变量X和Y的一些数据对， (xi,yi) 可以看做是上面例子中第i个学生的数学成绩和英语成绩组成的数据对。现在我们从这n个数据对中任意选两个数据对 (xi,yi) 和 (xj,yj) 形成 [(xi,yi),(xj,yj)] ，其中i!=j且 [(xi,yi),(xj,yj)] 和 [(xj,yj),(xi,yi)] ，这样的对子一种有 N=n(n+1)2 种。对于任意的 [(xi,yi),(xj,yj)] ，若 xi>xj 且 yi>yj 或者 xi<xj 且 yi<yj 则称呼这样的对子是concordant，它们的个数记为P。 xi>xj 且 yi<yj 或者 xi<xj 且 yi>yj 则称呼这样的对子discordant，它们的个数记为Q。若 xi=xj 且 yi>yj 或者 xi=xj 且 yi<yj ，这样的对子个数记为 X0 。若 xi>xj 且 yi=yj 或者 xi<xj 且 yi=yj ，这样的对子个数记为 Y0 。若 xi=xj 且 yi=yj ，这样的对子的个数记为 (XY)0 。因此N=P+Q+ X0 + Y0 + (XY)0 。

有了这些概念之后我们就可以来计算krocc了，下面就是其公式。

krocc=P−Q(P+Q+X0)(P+Q+Y0)−−−−−−−−−−−−−−−−−−−−−√

从这里的概念的解释我们可以了解到，krocc也是评价两个变量的等级相关的，这里就不再累述了。

3.PLCC

PLCC的全称是Pearson product-moment correlation coefficient。因为它相对比较简单，所以我这里直接给出它的公式：

plcc=COV(X,Y)δXδY

对概率论和数理统计还比较熟悉的同学可以知道这就是我们学过的线性相关系数，若我们把X和Y看做两个随机变量，则分母是随机变量X和Y的协方差，分子是它们的标准差的乘积。plcc就是来评价两组数据的线性相关关系的。若其绝对值越接近于1，则其之间的关系就越可以用一个线性直线方程来表示。多余的我就不再累述了。

4.rMSE

rMSE的全称是root mean square error。其实他就是MSE(均方误差)的平方根。如果拿我举得的那个例子来说的话，那它的计算公式是：

rMSE=∑ni=1(xi−yi)2n−−−−−−−−−−−−−√

其中 (xi,yi) 是对应的数学成绩和英语成绩的数据对。直面理解rMSE就是数据错误平方均值的平方根。这里只是一种离散情况的简单解释，更复杂的情况读者可以参阅我参考资料中的解释和其它方面的资料。当然其值应该越小越好，这样它的错误就小啊！而上面的三个系数对于一种质量评价算法来说应该越大越好，这样的话预测值就和主观评价值越接近，这样的质量评价算法肯定好啊！

最后再说几句，srocc，krocc和plcc在matlab中可以直接利用函数corr计算。但是在计算plcc和rMSE的时候需要先将要比较的两组数据或者两个变量的数据(这个我也只是大概了解一下，想详细了解的同学要自己查资料了)进行一下非线性回归分析或拟合之类的操作然后再去算。matlab中可以用nlinfit这个函数。
参考资料：
1:https://statistics.laerd.com/statistical-guides/spearmans-rank-order-correlation-statistical-guide.php

2:http://www.epixanalytics.com/modelassist/AtRisk/Model_Assist.htm#Probability_theory_and_statistics/The_basics/Probability_theorems/Useful_concepts/Rank_Order_Correlation_Coefficient.htm

3:http://blog.csdn.net/wsywl/article/details/5859751

4:https://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient

5:http://blog.csdn.net/wsywl/article/details/5889419

6:https://onlinecourses.science.psu.edu/stat509/node/158

7:https://en.wikipedia.org/wiki/Kendall_rank_correlation_coefficient

8:http://blog.csdn.net/wsywl/article/details/5727327

9:https://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient

10:https://en.wikipedia.org/wiki/Mean_squared_error

11:https://en.wikipedia.org/wiki/Root-mean-square_deviation