从K-Means到Capsule
整体上来看,Capsule算法的细节不是很复杂,对照着它的流程把Capsule用框架实现它基本是没问题的。所以,困难的问题是理解Capsule究竟做了什么,以及为什么要这样做,尤其是Dynamic Routing那几步。
为什么我要反复对Capsule进行分析?这并非单纯的“炒冷饭”,而是为了得到对Capsule原理的理解。众所周知,Capsule给人的感觉就是“有太多人为约定的内容”,没有一种“虽然我不懂,但我相信应该就是这样”的直观感受。我希望尽可能将Capsule的来龙去脉思考清楚,使我们能觉得Capsule是一个自然、流畅的模型,甚至对它举一反三。
在《揭开迷雾,来一顿美味的Capsule盛宴》中,笔者先分析了动态路由的结果,然后指出输出是输入的某种聚类,这个“从结果到原因”的过程多多少少有些望文生义的猜测成分;这次则反过来,直接确认输出是输入的聚类,然后反推动态路由应该是怎样的,其中含糊的成分大大减少。两篇文章之间有一定的互补作用。
Capsule框架 ↺
与其说Capsule是一个具体的模型,倒不如说Capsule是一个建模的框架,而框架内每个步骤的内容,是可以自己灵活替换的,而Hinton所发表的论文,只是一个使用案例。
这是一个怎样的框架呢?
特征表达 ↺
Capsule模型中,每个特征都是用一个向量(即Capsule,胶囊)来表示的。
当然,对于关注新闻的读者来说,这已经不是什么新消息。可能读者会有疑问:用向量来表示特征有什么稀奇的,本来神经网络的特征输入不就是一个向量吗?原来神经网络(MLP)的每一层输入是一个向量x∈Rnx∈Rn,然后输出是y=Activation(Wx+b)∈Rky=Activation(Wx+b)∈Rk,我们就将xx的每一个分量都看成一个特征,那么每个特征都是标量了。而所谓的特征向量化后,那么每一层的输入变成了x∈Rn×dxx∈Rn×dx,然后输出是y=Routing(x)∈Rk×dyy=Routing(x)∈Rk×dy,这时候的输入xx也看成是nn个特征,但每个特征都是一个dxdx维向量;输出yy则看成是kk个特征,每个特征是一个dydy维向量。换一个角度看,其实就是说MLP每一层的输入输出由单个的向量变成了向量的集合(矩阵)。
或者我们可以将它换一个名称,叫做“特征的分布式表示”。也许有读者看到了“分布式表示”,会想起NLP中的词向量。没错,词向量一开始确实叫做“分布式表示”(Distributed Representation),而笔者看到Capsule的这一特点,第一反应也就是词向量。我们可以用词向量代替one hot来表示一个词,这样表达的信息就更为丰富了,而且所有的词都位于同一向量空间,方便后续处理。
此外,事实上图像中早也有这样的例子,众所周知彩色图像一般有RGB三个通道,每个通道256个选择,所以一共可以表达2563=167772162563=16777216种颜色(约1700万),为什么不直接用1700万个数字来分别表示这1700种颜色,而要分开3组,每组256个数字呢?这其实也是一种分布式表示,这样可以更好地表达色彩的多样性(比如红色的相近颜色是什么色?也许有人说橙色,也有人说紫色,也有可能是粉红,单一一个数字难以表达多种的相似性,而分组后则可以。)。更进一步说,我们在对图像不断进行卷积操作时,所得结果的通道维度,其实就是图像特征的一种分布式表示了。
特征组合 ↺
Capsule的第二个特点,是通过聚类来组合特征。
组合与表达 ↺
通过将底层特征组合为上层的特征,是跟我们的认知规律是相符的。在NLP中,我们有“字-->词-->句-->段”的层层组合;在图像中,我们也有“点-->线-->面-->体”的层层组合。面对新事物(上层特征),我们总会将它分解为我们熟悉的一些事物(底层特征),然后脑海里将这些事物映射到这个新事物(特征组合)。
对于我们来说,这个分解和组合的过程,不一定有什么目的,而只是为了用我们自己的方式去理解这个新事物(在大脑中形成良好的特征表达)。这也就能理解Hinton诟病深度学习、发展Capsule的原因之一了,因为他觉得现在深度学习的模型针对性太强(比如MNIST分类模型就只能做单个数字的识别,多个数字的识别就要重新构建数据集、重新设计并训练模型),而事实上,我们的根本目的并不是单纯地做任务,而是通过任务形成良好的、普适的特征表达,这样才有可能形成真正的人工智能。
特征间聚类 ↺
那么,怎么完成这个组合的过程呢?试想一下,两个字为什么能成为一个词,是因为这两个字经常“扎堆”出现,而且这个“堆”只有它们俩。这就告诉我们,特征的聚合是因为它们有聚类倾向,所以Capsule把聚类算法融入到模型中。
要注意,我们以前所说的聚类,都是指样本间的聚类,比如将MNIST的图片自动聚类成10个类别,或者将Word2Vec训练而来的词向量聚类成若干类,聚类的对象就是一个样本(输入)。而Capsule则设想将输入本身表示为若干个特征向量,然后对这些向量进行聚类(特征间的聚类),得到若干中心向量,接着再对这些中心向量聚类,层层递进,从而完成层层抽象的过程。这是一种特征间的聚类。
现在问题就来了。既然是聚类,是按照什么方法来聚类的呢?然后又是怎么根据这个聚类方法来导出那个神奇的Dynamic Routing的呢?后面我们会从K-Means出发来寻根问底,现在让我们先把主要思路讲完。
特征显著性 ↺
通过特征的组合可以得到上层特征,那如何对比特征的强弱程度呢?Capsule的答案是:模长。这就好比在茫茫向量如何找出“突出”的那个?只需要看看谁更高就行了。因此通过特征向量的模长来衡量它自己的“突出程度”,显然也是比较自然的选择。此外,一个有界的度量也是我们希望的,因此我们对特征向量做一个压缩:
压缩的方案并不唯一,这里就不展开了。 不过我在实验过程中,发现将1替换为0.5能提升性能。
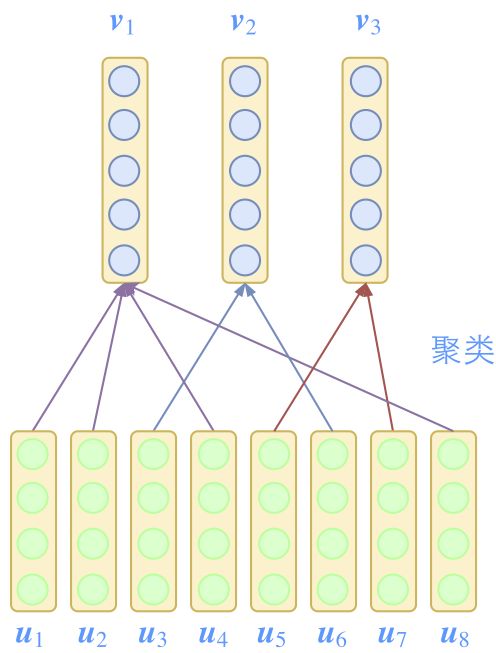
为了突出模长的这一含义,也需要在设计模型的时候有所配合。如图,尽管v1v1所代表的类所包含的特征向量u1,u2,u4,u8u1,u2,u4,u8的模长均比较小,但因为成员多(“小弟多”),因此v1v1的模长也能占优(“势力大”)。这说明,一个类要突出,跟类内向量的数目、每个类内向量本身的模长都有关联。后面我们也会看到Capsule是如何体现这一点的。
K-Means新探 ↺
既然本文不断强调Capsule是通过聚类来抽象特征的,那么就有必要来细谈一下聚类算法了。Capsule所使用的聚类算法,其实是K-Means的变种。聚类算法有很多,理论上每种聚类算法都是可能的,然而要将聚类算法嵌入到Capsule中,还需要费上一点周折。
聚类目标 ↺
K-Means聚类本质上是一种“中心聚类方法”——聚类就是找类别中心。为了定义中心,我们就需要一个相近程度的度量,常用的是欧氏距离,但这并不是唯一的选择。所以这里我们干脆在一个更加一般的框架下介绍K-Means:K-Means希望把已有的数据u1,u2,…,unu1,u2,…,un无监督地划分为kk类,聚类的方法是找出kk个聚类中心v1,v2,…,vkv1,v2,…,vk,使得类内间隔最小:
这里 dd 代表了相近程度的度量,所以这个式子的意思很简单,就是说每个 uiui 只属于跟它最相近的那一类,然后将所有类内距离加起来,最小化这个类内距离:
注:显然,聚类的结果依赖于 dd的具体形式,这其实就告诉我们:无监督学习和有监督学习的差别,在于我们跟模型“交流”的方法不同。有监督学习中,我们通过标注数据向模型传达我们的意愿;在无监督学习中,我们则通过设计适当的度量 dd来完成这个过程。
求解过程 ↺
怎么去最小化LL来求出各个中心呢?如果读者不希望细细了解推导过程,可以跳过这一节,直接看下一节。
因为LL中有minmin这个操作,所以直接求它的梯度会有困难(不是不能求,而是在临界点附近不好处理),事实上有很多类似的问题没能得到很好的解决,都是因为它们的loss中有minmin(日后有机会我们再谈这个事情。)。
然而,这里我们可以“软化”这个LL,使得它可以求导。因为我们有一个很漂亮的公式
注:如果取 K=1K=1,显然括号里边就是softmax的分母,这也就是softmax的由来了——它是“soft”加“max”——“软的最大值”。
而我们有
因此我们就得到
现在这个近似的loss在全局都光滑可导了。因此我们可以尝试求它的梯度
这里
我们已经指明了是对 jj 所在的维度来归一化。为了求出一个极小值,我们希望让 ∂L/∂vj=0∂L/∂vj=0 ,但得到的方程并不是简单可解的。因此,可以引入一个迭代过程,假设 v(r)jvj(r) 是 vjvj 的第 rr 次迭代的结果,那么我们可以让
如果可以从上述方程解出 v(r+1)jvj(r+1) ,那么就可以从中得到一个迭代格式。
欧氏距离 ↺
现在就可以把我们选择的度量代入(8)(8)式进行计算了。我们可以看一个最基本的例子:d(ui,vj)=∥ui−vj∥2d(ui,vj)=‖ui−vj‖2,这时候就有
根据 (8)(8) 式得到 0=2∑i=1nc(r)ij(v(r+1)j−ui)0=2∑i=1ncij(r)(vj(r+1)−ui) ,从而我们可以解出
如果取 K→+∞K→+∞ ,那么 c(r)ijcij(r) 非0即1,所以上式就是说(读者可以自己把证明补充完整)
v(r+1)jvj(r+1)是距离 v(r)jvj(r)最近的那些 uiui的平均值。
这就得到了我们平时说的K-Means聚类算法。
内积相似度 ↺
欧氏距离并不适合用在Capsule中,这是因为欧氏距离得到的中心向量是类内的向量的平均,这样类内向量越多,也不会导致中心向量的模越长,这不满足我们前面说的“小弟越多,势力越大”的设计。
什么距离比较适合呢?在论文《Dynamic Routing Between Capsules》中有一段话:
The initial coupling coefficients are then iteratively refined by measuring the agreement between the current output vjvj of each capsule, jj, in the layer above and the prediction u^j|iu^j|i made by capsule ii.
The agreement is simply the scalar product aij=vj⋅u^j|iaij=vj⋅u^j|i ...
对应到本文,大概的意思是用内积⟨ui,vj⟩⟨ui,vj⟩作为相似度的度量,也就是说,d(ui,vj)=−⟨ui,vj⟩d(ui,vj)=−⟨ui,vj⟩。但仔细思考就会发现问题,因为这样的dd是无下界的!无下界的函数我们不能用来做loss,所以我一直被这里困惑着。直到有一天,我觉得可以将vjvj先归一化,然后再算内积,这样一来实际上是:
现在对于固定的 uiui ,不管 vjvj 怎么变, d(ui,vj)d(ui,vj) 就有下界了。所以这样的 dd 是可以用来作为loss的,代入 (8)(8) 式算,最终得到的结果(有一定难度,建议读者动手试试)是
也就是说 v(r+1)jvj(r+1) 和 ∑i=1nc(r)ijui∑i=1ncij(r)ui 的方向是一样的,但这不能说明它们两个是相等的。然而,这也意味着我们确实可以简单地取
如果取 K→+∞K→+∞ 的极限,那么就是说
v(r+1)jvj(r+1)是距离 v(r)jvj(r)最近的那些 uiui的和。
由于现在是求和,就可以体现出“小弟越多,势力越大”的特点了。(注意,这里和欧氏距离那都出现了“最近”,两个最近的含义并不一样,因为所选用的dd不一样。)
动态路由 ↺
经过漫长的准备,Dynamic Routing算法已经呼之欲出了。
按照第一部分,我们说Capsule中每一层是通过特征间聚类来完成特征的组合与抽象,聚类需要反复迭代,是一个隐式的过程。我们需要为每一层找到光滑的、显式的表达式
基本步骤 ↺
假设Capsule的输入特征分别为u1,u2,…,unu1,u2,…,un,然后下一层的特征向量就是v1,v2,…,vkv1,v2,…,vk,它就是前一层nn个向量聚为kk类的聚类中心,聚类的度量是前面的归一化内积,于是我们就可以写出迭代过程:
初始化 vj=v(0)jvj=vj(0)
迭代 rr次:
vj=vj/∥vj∥vj=vj/‖vj‖;
如果 j=argmaxj=1,…,k⟨ui,vj⟩j=argmaxj=1,…,k⟨ui,vj⟩,那么 cij=1cij=1,否则 cij=0cij=0;
vj=∑icijuivj=∑icijui;
返回 squash(vj)squash(vj)。
这个版本是容易理解,但由于存在argmaxargmax这个操作,我们用不了梯度下降,而梯度下降是目前求模型其他参数的唯一方法。为了解决这个问题,我们只好不取K→+∞K→+∞的极限,取一个常数K>0K>0,然后将算法变为
初始化 vj=v(0)jvj=vj(0)
迭代 rr次:
vj=vj/∥vj∥vj=vj/‖vj‖;
cij=softmaxj(⟨ui,Kvj⟩)cij=softmaxj(⟨ui,Kvj⟩);
vj=∑icijuivj=∑icijui;
返回 squash(vj)squash(vj)。
然而这样又新引入了一个参数KK,咋看上去KK太大了就梯度消失,KK太小了就不够准确,很难确定。不过后面我们将会看到,直接让K=1K=1即可,因为K=1K=1的解空间已经包含了任意KK的解。最终我们可以得到
初始化 vj=v(0)jvj=vj(0)
迭代 rr次:
vj=vj/∥vj∥vj=vj/‖vj‖;
cij=softmaxj(⟨ui,vj⟩)cij=softmaxj(⟨ui,vj⟩);
vj=∑icijuivj=∑icijui;
返回 squash(vj)squash(vj)。
有意思的是,最后导出的结果,不仅跟Hinton的原始论文《Dynamic Routing Between Capsules》有所出入,跟我前一篇介绍也有出入。其中,最明显的差别是在迭代过程中用vj/∥vj∥vj/‖vj‖替换了squash(vj)squash(vj),仅在最后输出时才进行squash。实验表明这有助于提升特征的表达能力,它在我的前一文的数字实验(单数字训练,双数字预测)中,能达到95%以上的准确率(原来是91%)。
三种症状 ↺
这样就完了?远远还没有。我们还要解决好几个问题。
1、如何做好类别初始化? 因为聚类结果跟初始化有关,而且好的初始化往往是聚类成功的一大半。现在我们要将聚类这个过程嵌入到模型中,作为模型的一部分,那么各个v(0)jvj(0)应该怎么选取呢?如果同一初始化,那么无法完成聚类过程;如果随机初始化,那又不能得到确定的聚类结果(就算类中心向量不变,但是类的顺序也可能变化)。
2、如何识别特征顺序? 我们知道,聚类的结果跟样本的顺序是无关的,也就是说,如果将输入向量的顺序打乱,聚类的结果还是一样的。对于样本间的聚类,这是一个优点;然而如果是特征间的聚类,那么就有可能不妥了,因为不同顺序的特征组合可能代表不同的含义(就好比词序不同,句子含义也会不同),如果都给出一样的结果,那么就丧失了特征的序信息了;
3、如何保证特征表达能力? 动态路由将上层Capsule作为底层Capsule的聚类结果,每个类可能包含多个特征向量,但如果仅仅用类中心向量整个类的整体特征(上层特征),会不会降低了上层Capsule的特征表达能力?
一个对策 ↺
有意思的是,以上三个问题都可以由同一个方法解决:加变换矩阵。
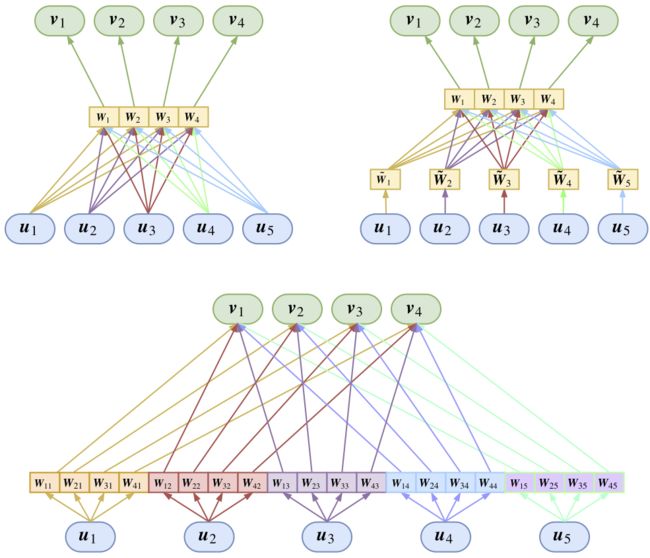
首先,为了模型的简洁性,我们将所有uiui的和平均分配到每个类中作为v(0)jvj(0)。那怎么分辨出各个不同的类呢?我们在输出到每个类之前,给每个类都配一个变换矩阵WjWj,用来分辨不同的类,这时候动态路由变成了:
初始化 vj=1k∑i=1nWjuivj=1k∑i=1nWjui
迭代 rr次:
vj=vj/∥vj∥vj=vj/‖vj‖;
cij=softmaxj(⟨Wjui,vj⟩)cij=softmaxj(⟨Wjui,vj⟩);
vj=∑icijWjuivj=∑icijWjui;
返回 squash(vj)squash(vj)。
这就是我前一篇介绍中所说的共享权重版的Capsule。细细斟酌就会发现,引入训练矩阵WjWj是个非常妙的招数,它不仅解决了聚类的初始化问题(同一初始化经过矩阵WjWj映射为不同初始化),而且通过WjWj可以改变uiui的维度,从而也就改变了聚类后的中心向量的维度,这样也就能保证中心向量的特征表达能力(可以升高或降低维度)。还有,以前我们做分类,是用一个向量做内积然后softmax的方式,也就是用一个向量代表一个类,现在则相当于用一个矩阵来代表一个类,当然也就可以表达更丰富的类信息。此外还有一个好处,那就是我们有⟨Wjui,Kvj⟩=⟨(KWj)ui,vj⟩⟨Wjui,Kvj⟩=⟨(KWj)ui,vj⟩,也就是说它相当于把前面的参数KK也包含了,从而我们可以放心设K=1K=1而不用担心准确性不够——如果有必要,模型会自己去调整WjWj达到调整KK的效果!
现在只剩下最后一个问题了:识别输入特征的顺序。跟识别每一个类一样,我们也可以给每个输入都配一个变换矩阵W~iW~i,用来分辨不同位置的输入,这样一来动态路由变为
初始化 vj=1k∑i=1nWjW~iuivj=1k∑i=1nWjW~iui
迭代 rr次:
vj=vj/∥vj∥vj=vj/‖vj‖;
cij=softmaxj(⟨WjW~iui,vj⟩)cij=softmaxj(⟨WjW~iui,vj⟩);
vj=∑icijWjW~iuivj=∑icijWjW~iui;
返回 squash(vj)squash(vj)。
如果觉得这样太累赘,那么可以把WjW~iWjW~i替换成一个整体矩阵WjiWji,也就是对每对指标(i,j)(i,j)都配上一个变换矩阵,这样的好处是整体更简单明了,缺点是矩阵数目从n+kn+k个变成了nknk个:
初始化 vj=1k∑i=1nWjiuivj=1k∑i=1nWjiui
迭代 rr次:
vj=vj/∥vj∥vj=vj/‖vj‖;
cij=softmaxj(⟨Wjiui,vj⟩)cij=softmaxj(⟨Wjiui,vj⟩);
vj=∑icijWjiuivj=∑icijWjiui;
返回 squash(vj)squash(vj)。
这便是全连接版的动态路由。然而并不是每次我们都要分辨不同位置的输入,对于变长的输入,我们就很难给每个位置的输入都分配一个变换矩阵,这时候共享版的动态路由就能派上用场了。总的来说,全连接版和共享版动态路由都有其用武之地。
结语 ↺
笔者通过这两篇“浩浩荡荡”(哆里哆嗦)的博文,来试图解读Hinton大力发展的Capsule模型,然而作者水平有限,其中不当之处,还请读者海涵。
个人认为,Capsule的确是新颖的、有前景的的研究内容。也许它不一定(但也是有可能的)是未来的发展方向,但细细品味它,仍足以让我们获益良多。
现在回顾文章开头的目标——企图让Capsule看起来更加自然一些,不知道读者现在的感受如何?个人感觉是,之前经过这样的解析,Capsule也不是那么超然物外,而是一个大胆的尝试——Hinton大胆地将聚类的迭代过程融入到神经网络中,因此诞生了Capsule。
那是不是说,可以考虑将其他比较直观的算法也融入到里边,从而造就其他有意思的玩意?让我们拭目以待。
转载到请包括本文地址:https://kexue.fm/archives/5112/