Java实现几种最短路径问题

前言

最短路径问题在现实处处可见，而且针对不同的情形都需要具体分析才会找到最好解法。

最短路径Floyd算法

一支部队急行军，要经过A,B,C,D据点，这四个据点之间有些之间有路到达，有些没有。为了最大的节约时间，部队指挥部需要知道任意两个据点之间的最短时间。以下是两两之间所花的时间(如下图所示):

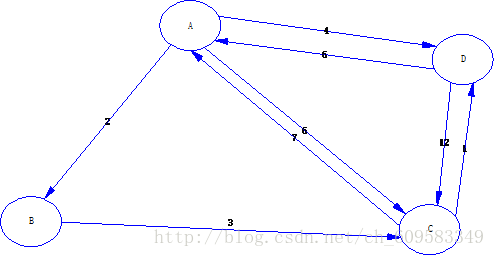
那么如何才能让两个据点之间花的时间变短？加入第三个据点即可。因此判断条件就出来了：
两个据点之间花费的时间如果比加入第三个据点的时间长，那么两个据点之间的最短时间即是加入第三个据点的时间之和。
这样Floyd算法的Java实现如下（核心代码就是上面的判断，边的权值全部提前赋值）：

public class Floyd {

      /**
     * @param graph 图的邻接矩阵
     * @param n 代表顶点的个数
     * @return
     */
    public int[][] floyd(int[][] graph,int n){
          int[][] edge = new int[n][n];
          for(int i=0;ifor(int j=0;jfor(int k=0;kfor(int i=0;ifor(int j=0;jif(edge[i][j]>edge[i][k]+edge[k][j])
                          edge[i][j]=edge[i][k]+edge[k][j];
                  }
              }
          }
          return edge;
      }
}

Floyd算法容易理解，并且可以算出任意两个点之间的最短距离。不难得出，Floyd算法的时间复杂度为O(n3)，空间复杂度为O(n2)，n为顶点的个数。

单源最短路径Dijkstra

还有一种常见的问题，也就是单源最短路径。求出1号顶点到其它顶点的最短距离：

类似Floyd算法，我们在核心代码里面直接就给出图的邻接矩阵，避免不必要的代码。
public class Dijiskra {

      public int[] dijsktra(int[][] edge){
      //得到顶点个数
          int vartex = edge.length;
         //标记
          int flag = 0;
        //记录某个顶点有没有访问到
          int[] mark = new int[vartex];
    //这里求的是从第一个顶点到其它顶点的最短距离
          mark[0]=1;
          int[] distance = new int[vartex];
    //最开始默认的都是边的值，这里传进来就得事先做好处理，比如两个顶点之间不可达，那么久应该赋值为一个很大的数
          for(int i=0;idistance[i]=edge[0][i];
          }
    //核心代码
          for(int i=1;iint min = Integer.MAX_VALUE;
              for(int j=0;jif(mark[j]==0&&distance[j]<min){
                        min=distance[j];
                        flag=j;
                    }
               }
              mark[flag]=1;
              for(int k=0;kif(distance[k]>distance[flag]+edge[flag][k]){
                      distance[k]=distance[flag]+edge[flag][k];
                  }
              }

          }
          return distance;
      }
}

该算法同样和顶点关系密切，其时间复杂度为O(n2)，空间复杂度也只需要存储图的邻接矩阵或者邻接链表即可。