查找--深入理解一致性哈希算法
注:本篇博客只是讲述了一致性哈希的思想,我们会在之后讲述分布式哈希表以及一致性哈希的一种实现(Chord算法)。
什么是一致性哈希算法?
引用自维基百科:
一致性哈希是一种特殊的哈希算法。在使用一致哈希算法后,哈希表槽位数(大小)的改变平均只需要对 K/n个关键字重新映射,其中K是关键字的数量,n是槽位数量。然而在传统的哈希表中,添加或删除一个槽位几乎需要对所有关键字进行重新映射。
总结:一致性哈希算法主要关注的是在分布式架构中,当节点数目发生变化的时候(增加/删除),怎样使再哈希的数据量最少。
一致性哈希的引出
在分布式系统中,节点的宕机、某个节点加入或者移出集群是常事。对于分布式存储而言,假设存储集群中有10台机器(node),如果采用传统Hash方式对数据分片(item)(即数据根据哈希函数映射到某台机器上存储),哈希函数应该是这样的:hash(item) % 10。根据上面的介绍,当node数发生变化(增加、移除)后,数据会被重新“打散”,导致大部分数据不能落到原来的节点上,从而导致大量数据需要迁移,而这种移动会造成网络的负载。
那么,一个亟待解决的问题就变成了:当node数发生变化时,如何保证尽量少引起迁移呢?即当增加或者删除节点时,对于大多数item,保证原来分配到的某个node,现在仍然应该分配到那个node,将数据迁移量降到最低。
一致性哈希的原理及优劣
传统的Hash算法将对应的key哈希到一个具有2^32次方(int)个桶的空间中,即0~(2^32)-1的数字空间中。现在我们可以将这些数字头尾相连,想象成一个闭合的环形。也就是将传统的线性哈希表构造成环形哈希表。
我们来看一下如何将数据映射到环形哈希表上:
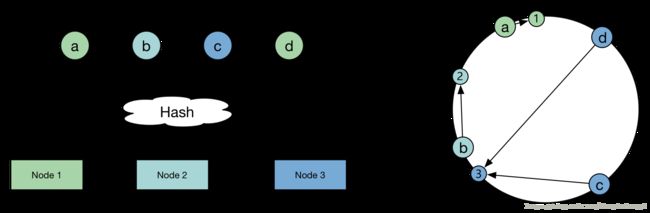
如上图,有三台机器(node),四个数据项(item),每台机器对应着一个n位的ID(采用机器的IP或者机器唯一的别名作为哈希函数的输入值),并且映射到环中,每个查询键,也是一个n位的ID,节点的ID和查询键对应着相同的映射空间。三台机器将整个环分割成了三部分,分别是(1,3),(3,2),(2,1)。
机器1负责存储落在(2,1)范围内的数据,机器2负责存储落在(3,2)范围内的数据…..
也就是说,对数据进行Hash时,数据的地址会落在环上的某个点上,数据就存储在该点的顺时针方向上的那台机器上。
这种数据存储的方式,相比于普通哈希方式,有明显的优势:当添加新机器或者删除机器时,不会影响到全部数据的存储,而只是影响到这台机器上所存储的数据(落在这台机器所负责的环上的数据)。
而这种思想,也就是一致性哈希。我们举个例子来感受一下使用一致性哈希的好处:
比如,机器1被移除了,那落在(2,1)范围内的数据全部需要由机器3来存储,也就只影响到落在(2,1)这个范围内的数据。同时,扩容也很方便,比如在(1,3)这段环上再添加一台机器4,只需要将3上的一部分数据拷贝到机器4上即可。
虽然一致性Hash算法解决了节点变化导致的数据迁移问题,但是,我们回过头来再看看数据分布的均匀性:
数据被传统的哈希算法“打散”后,是可以比较均匀分布的。但是引入一致性哈希算法后,为什么就不均匀呢?数据本身的哈希值并未发生变化,变化的是判断数据哈希后应该落到哪个节点的算法变了。
这三个节点Hash后,在环上分布不均匀,导致了每个节点实际占据环上的区间大小不一,数据随机映射到每个节点的概率就有较大差别,换个说法,也就是不能实现较好的负载均衡。
举个例子:机器1的配置很高,性能很好,而机器3的配置很低。但是,如上图,大部分数据由于某些特征都哈希到(1,3)这段环上,直接就导致了机器3的存储压力很大。
虚拟节点的引入
当我们将node进行哈希后,这些值并没有均匀地落在环上,因此,最终会导致,这些节点所管辖的范围并不均匀,最终导致了数据分布的不均匀。
为了解决一致性哈希的不足,从而引入了虚拟节点的概念。
引入虚拟节点,可以有效地防止物理节点(机器)映射到哈希环中出现不均匀的情况。比如上图中的机器1、2、3都映射在环的左半边上。
一般,虚拟节点会比物理节点多很多,并可均衡分布在环上,从而提高负载均衡的能力。
- 如果虚拟节点与物理机器映射得好,某一台物理机器宕机后,其上的数据可由其他若干台物理机器共同分担;
- 如果新添加一台机器,它可以对应多个不相邻环段上的虚拟节点,从而使得Hash的数据存储得更分散。
如何判定一致性哈希算法的好坏?
- 平衡性(Balance):平衡性是指哈希的结果能够尽可能分布到所有的缓冲(服务器节点)中去,这样可以使得所有的缓冲空间都得到利用,很多哈希算法都能够满足这一条件;
- 单调性(Monotonicity):单调性是指如果已经有一些内容通过哈希分派到了相应的缓冲中,又有新的缓冲加入到系统中,哈希的结果应能够保证原有已分配的内容可以被映射到原有的或者新的缓冲中去,而不会被映射到旧的缓冲集合中的其他缓冲区;
- 分散性(Spread):在分布式环境中,终端有可能看不到所有的缓冲,而是只能看到其中的一部分。当终端希望通过哈希过程将内容映射到缓冲上时,由于不同终端所见的缓冲范围有可能不同,从而导致哈希的结果不一致,最终的结果是相同的内容被不同的终端映射到不同的缓冲区中。这种情况显然是应该避免的,因为它导致相同内容被存储到不同缓冲中去,降低了系统存储的效率。分散性的定义就是上述情况发生的严重程度。好的哈希算法应能够尽量避免不一致的情况发生,也就是尽量降低分散性;
- 负载(Load):负载问题实际上是从另一个角度看待分散性问题。既然不同的终端可能将相同的内容映射到不同的缓冲区中,那么对于一个特定的缓冲区而言,也可能被不同的用户映射为不同的内容。与分散性一样,这种情况也是应当避免的,因此好的哈希算法应能够尽量降低缓冲的负荷。
注:对于第四点来说,好的一致性哈希算法,应该将同一用户的请求映射到相同的机器上,因为一个缓冲区始终处理同一个用户的请求是比较容易实现的(Cookie),如果将不同用户的不同请求映射到相同的缓冲区中,既有可能增大机器的负载,而且不容易实现。
总结
- 熟悉一致性哈希算法的特点及原理;
- 熟悉一致性哈希算法的优劣与改进(虚拟节点);
- 掌握为什么会出现一致性哈希算法;
- 了解一致性哈希算法的另一种改进(线性空间的引入)—详见一致性哈希算法的理解与实践。
参考阅读
分布式哈希算法
一致性哈希算法的理解与实践
一致性哈希算法学习及JAVA代码实现分析
每天进步一点点—五分钟理解一致性哈希算法(consistent hashing)