Minimum Edit Distance 算法原理及实现
Minimum Edit Distance(最小编辑距离)算法可以用于计算单词相似度、拼写错误检查,以及翻译中的双语对齐。
最小编辑距离指的是源字符串X变换为目标字符串Y需要的基本字符操作(增加,删除,替换)的代价之和。
如下图[1]中,源串intension到目标串execution最少需要删除1个字符,增加1个字符,替换3个字符

Levenshtein 距离定义了两种代价计算方式:
1)增加、删除、替换的代价均为1
2)增加、删除的代价为1,替换(等价于先删除再增加)的代价为2
我们使用第2)种代价计算方式,则删除intention->excution的最小编辑距离为1+1+2*3=8
最小编辑距离的计算实际上是个从起点(源串X)到目的地(目标串Y)的最短路径搜索问题,因此可以使用动态规划算法来解决。
用 D [ i , j ] D[i,j] D[i,j]表示源串中的前 i i i个字符 X [ 1 ⋯ i ] X[1\cdots i] X[1⋯i] 和目标串中的前 j j j个字符 Y [ 1 ⋯ j ] Y[1\cdots j] Y[1⋯j]的最小编辑距离,则:
D [ i , j ] = m i n { d e l _ c o s t ( X [ i ] ) + D [ i − 1 , j ] D [ i , j − 1 ] + a d d _ c o s t ( Y [ j ] ) D [ i − 1 , j − 1 ] + s u b _ c o s t ( X [ i ] , Y [ j ] ) D[i,j]=min \begin{cases} del\_cost(X[i])+D[i-1,j]\\ D[i,j-1]+add\_cost(Y[j]) \\ D[i-1,j-1]+sub\_cost(X[i],Y[j]) \end{cases} D[i,j]=min⎩⎪⎨⎪⎧del_cost(X[i])+D[i−1,j]D[i,j−1]+add_cost(Y[j])D[i−1,j−1]+sub_cost(X[i],Y[j])
其代码(下载)实现如下:
import numpy as np
def del_cost(source_i):
return 1
def add_cost(target_j):
return 1
def sub_cost(source_i, target_j):
if source_i == target_j:
return 0
return del_cost(source_i) + add_cost(target_j)
def min_edit_distance(source: str, target: str):
s_len = 0
t_len = 0
if source:
s_len = source.__len__()
if target:
t_len = target.__len__()
if 0 == s_len and 0 == t_len:
return 0
D = np.zeros((s_len+1, t_len+1))
D[0,0]=0
for i in range(1,s_len+1):
D[i,0]=del_cost(source[i-1])+D[i-1,0]
for j in range(1,t_len+1):
D[0,j]=D[0,j-1]+add_cost(target[j-1])
for i in range(1,s_len+1):
for j in range(1,t_len+1):
left = D[i,j-1] + add_cost(target[j-1])
up = del_cost(source[i-1]) + D[i-1,j]
left_up_corner= D[i-1,j-1]+ sub_cost(source[i-1],target[j-1])
D[i,j]=min(left,up,left_up_corner)
#print(D)
return D[s_len,t_len]
然后我们用它计算intention和execution的最小编辑距离
source = "intention"
target = "execution"
mde = min_edit_distance(source, target)
print(mde)
输出为8,可见其能正确计算两个字符串的最小编辑距离。
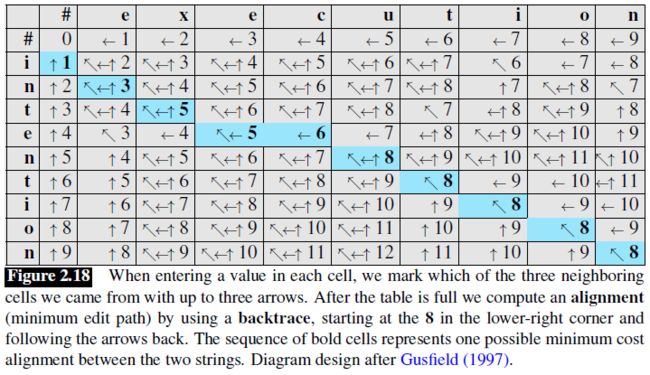
整个动态规划的过程实际就是填下图的这张表[1],源串为intention,目标串为execution,如果我们在填表的过程中记录了每个状态的回溯指针(图中的箭头),那么我们可以从最终状态沿着记录的回溯路径回溯,从而找到一种文本对齐的方法。
相同代价的路径可能不止一条,图中黑体数字表示了一种可能的路径。值得注意的是,如果路径上连续的两个状态在同一行,说明这是增加了一个字符,如果在同一列说明则是删除了一个字符,如果在对角上,说明是替换了一个字符(等价于先删再加,或者先加再删)。
参考文献:
[1] https://web.stanford.edu/~jurafsky/slp3/2.pdf