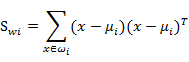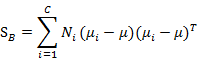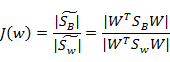LDA原理与fisherface实现

1.LDA数学原理

所谓分类器，一般是将输入空间X，根据需要划分的类别，将输入空间划分为一些互不相交的区域，这些区域的边界一般叫做决策面（decision boundaries）。预测函数的形式不同，会使得决策面或者光滑，或者粗糙。其中有一种比较特别的就是判别面是参数的线性函数的，称为线性决策面，形成的分类器就是线性分类器。

LDA属于线性分类器（linear classifier），K-分类的话有K个线性函数： Yk(X)=WkX+wk0 Y k ( X ) = W k X + w k 0

其中 Wk W k 称为权向量或者法向量， wk0 w k 0 称为阈值或者偏置。对任一X 而言，代入共K 个线性函数中去，存在一个 Yα>=Yi(1<=i<=k) Y α >= Y i ( 1 <= i <= k ) ，则说明X属于第 α α 类。

LDA分类的原则：不同类别之间的距离越远越好，同一类别间的元素越近越好。

二分类直线（投影函数）： y=WTx y = W T x

设类别i 的原始中心点（均值） μi：μi=1/n∑x∈Dix μ i ： μ i = 1 / n ∑ x ∈ D i x ，（D_i 表示数据类别i 的点）

则类别i 投影后的中心点为 μi^：μi^=WTμi μ i ^ ： μ i ^ = W T μ i ；

类别i 投影后，同一类别内点之间的分散程度(方差)： Si^=∑y∈YI(y−μi^)2 S i ^ = ∑ y ∈ Y I ( y − μ i ^ ) 2 ；

则总的类别点之间的方差函数为： Sw=∑ki=1Si S w = ∑ i = 1 k S i

不同类别间的分散程度(方差)： SB=∑ki=1ni(μi−μ)(μi−μ)T S B = ∑ i = 1 k n i ( μ i − μ ) ( μ i − μ ) T ；对于二分类来说， SB=|μ1^−μ2^|2 S B = | μ 1 ^ − μ 2 ^ | 2 ；

则目标优化函数可以写成： J(w)=|μ1^−μ2^|2Si^2+S2^2 J ( w ) = | μ 1 ^ − μ 2 ^ | 2 S i ^ 2 + S 2 ^ 2 ，目标函数最大时， w w 即为所要求的特征向量组成的投影矩阵。

Si^2=∑x∈Di(wTx−wTμi)2=∑x∈DiwT(x−μi)(x−μi)Tw=wTSww S i ^ 2 = ∑ x ∈ D i ( w T x − w T μ i ) 2 = ∑ x ∈ D i w T ( x − μ i ) ( x − μ i ) T w = w T S w w

同样的将 J(w) J ( w ) 分子化为：

|μ1^−μ2^|2=wT(μ1−μ2)(μ1−μ2)Tw=wTSBw | μ 1 ^ − μ 2 ^ | 2 = w T ( μ 1 − μ 2 ) ( μ 1 − μ 2 ) T w = w T S B w

则优化函数化为：

J(w)=wTSBwwTSww J ( w ) = w T S B w w T S w w ，采用拉格朗日乘子法，将分母限制为1，作为限制条件，代入得到：

c(w)=wTSww−λ(wTSww) c ( w ) = w T S w w − λ ( w T S w w ) ，目标函数最大，则 dcdw=2SBw−2λSww=0 d c d w = 2 S B w − 2 λ S w w = 0 ；

得到 SBw=λSww S B w = λ S w w ，得到这个等式即求等式成立的 w w ，即为所求。（广义特征值）

若 Sw S w 可逆，等式两边同乘 S−1w S w − 1 ；得到 S−1wSBw=λw S w − 1 S B w = λ w ；

即 S−1wSB S w − 1 S B 的特征向量即为所求的 w w ；

又由前面 SB=(μ1−μ2)(μ1−μ2)T S B = ( μ 1 − μ 2 ) ( μ 1 − μ 2 ) T ； SBw=(μ1−μ2)(μ1−μ2)Tw=(μ1−μ2)λ′ S B w = ( μ 1 − μ 2 ) ( μ 1 − μ 2 ) T w = ( μ 1 − μ 2 ) λ ′ ；

代入得到 S−1wSBw=S−1wλw=S−1w(μ1−μ2)λ′ S w − 1 S B w = S w − 1 λ w = S w − 1 ( μ 1 − μ 2 ) λ ′ ；由于扩大缩小倍数不影响w 的值，所以：

ω=S−1w(μ1−μ2) ω = S w − 1 ( μ 1 − μ 2 )

对于k-类问题：

平面内找不到一个合适的向量，能够将所有的数据投影到这个向量而且不同类间合理的分开。所以我们需要增加投影向量w的个数（当然每个向量维数和数据是相同的，不然怎么投影呢），设w为：

w1、w2等是n维的列向量，n为每个数据的维度，所以w是个(n×k)的矩阵，这里的k其实可以按照需要随意选取，只要能合理表征原数据就好。x在w上的投影可以表示为：

y=WTx y = W T x

所以这里的y是k维的列向量，实现降维。

像上一节一样，我们将从投影后的类间散列度和类内散列度来考虑最优的w。与二分类相似，μi 依然代表类别i的中心， Sw S w 定义如下：

其中：

代表类别i的类内散列度，它是一个nxn的矩阵。

所有x的中心 μ μ 定义为：

类间散列度定义和上一节有较大不同：

代表的是每个类别到 μ μ 距离的加和，注意 Ni N i 代表类别i内x的个数，也就是某个人的人脸图像个数。

上面的讨论都是投影之间的各种数据，而J(w) 的计算实际是依靠投影之后数据分布的，所以有：

分别代表投影后的类别i的中心，所有数据的中心，类内散列矩阵，类间散列矩阵。与上节类似J(w) 可以定义为：

回想我们上节的公式J(w) ，分子是两类中心距，分母是每个类自己的散列度。现在投影方向是多维了（好几条直线），分子需要做一些改变，我们不是求两两样本中心距之和（这个对描述类别间的分散程度没有用），而是求每类中心相对于全样本中心的散列度之和。得到：

最后化为：

还是求解矩阵的特征向量，然后根据需求求矩阵 S−1wSB S w − 1 S B 的前k个特征值，取前k个特征值最大的特征向量，张成 W W 投影矩阵。

由于 S−1wSB S w − 1 S B 不是对称矩阵，所以求得的K个矩阵不是正交矩阵，这是LDA与PCA的最大区别。

fisherface方法与eigenface方法比较

Fisherfaces方法学习一个正对标签的转换矩阵，所以它不会如特征脸那样那么注重光照，但是光照对判别结果还是有影响的。鉴别分析是寻找可以区分人的面部特征。需要说明的是，Fisherfaces的性能也很依赖于输入数据。实际上，如果你对光照好的图片上学习Fisherfaces，而想对不好的光照图片进行识别，那么他可能会找到错误的主元，因为在不好的光照图片上，这些特征不优越。这似乎是符合逻辑的，因为这个方法没有机会去学习光照。[gm:那么采集图像时就要考虑光照变化，训练时考虑所有光照情况] 因此，这两种方法对光照都敏感。

Fisherfaces允许对投影图像进行重建，就像特征脸一样。但是由于我们仅仅使用这些特征来区分不同的类别，因此你无法期待对原图像有一个好的重建效果。[也就是eigenface把每个图片看成一个个体，重建时效果也有保证，而Fisherfaces把一个人的图像（一类图像）看成一个整体，那么重建时重建的效果则不是很好]。对于Fisherfaces方法我们将把样本图像逐个投影到Fisherfaces上。因此你可以获得一个好的可视效果。

2.LDA算法步骤

输入数据：数据集 D=(x1,y1),(x2,y2)......(xN,yN) D = ( x 1 , y 1 ) , ( x 2 , y 2 ) . . . . . . ( x N , y N ) ，其中 xi x i 为d维向量，共有N 个数据样本， yi y i 为分类信息， yiC1,C2,...,Cq y i C 1 , C 2 , . . . , C q ，共有q 个类，原始数据集size为(d×N)， 降维到的维度为k；

输出：降维后的样本集 D′ D ′ (k×N) ( k × N ) 。

步骤：

1)计算总体样本的平均值mean向量\mu ，以及第i 类别中样本的平均值 μi（d×1） μ i （ d × 1 ） ， (1<=i<=q) ( 1 <= i <= q )

2)计算类内散度矩阵： SW=∑qi=1Si=∑qi=1(xi,j−μi)(xi,j−μi)T S W = ∑ i = 1 q S i = ∑ i = 1 q ( x i , j − μ i ) ( x i , j − μ i ) T ，（d×d）其中 xi,j x i , j 为第i 类的元素，此协方差公式即为计算类内元素与类均值 μi μ i 的距离，即类内方差，分母

3)计算类间散度矩阵： SB=∑qi=1ni(μi−μ)(μi−μ)T S B = ∑ i = 1 q n i ( μ i − μ ) ( μ i − μ ) T ，（d×d）， ni n i 为每个类别的数据数量，m 为总数据的均值mean， μi μ i 为每个类别的数据的均值，计算协方差 SB S B 得到代表数据类间的距离，即类间方差，分子

4)计算矩阵 S−1WSB S W − 1 S B ，（d×d）得到其最大的个k特征值对应的k个特征向量 (w1,w2,...wk) ( w 1 , w 2 , . . . w k ) ，即为投影矩阵 W(d×k) W ( d × k ) ，

5)将样本集中的每个数据元素 xα x α 转化为新的样本数据： Zi=WTxα Z i = W T x α ,
(k×d×d×1)=k×1 ( k × d × d × 1 ) = k × 1 ；

6)得到LDA降维后的总体样本数据集： D′=(Z1,y1),(Z2,y2)......(ZN,yN) D ′ = ( Z 1 , y 1 ) , ( Z 2 , y 2 ) . . . . . . ( Z N , y N ) ， (k×N) ( k × N )

人脸识别： 得到了投影矩阵 WT W T ，将所要识别的人脸图像 Y Y 在这个投影矩阵 W W 方向上进行投影，得到一个k维的向量，即在新空间中的坐标向量 ZY Z Y ，将 ZY Z Y 与训练样本中得到的新的数据集 Zi Z i 进行欧式空间距离的计算，距离最小的数据所属的类别，即为识别的人脸所属的类别，即为匹配成功。（可以设定一个合适的距离阈值，阈值过大判断为新的人脸或者不是人脸）

LDA算法既可以用来降维，又可以用来分类，但是目前来说，主要还是用于降维。在我们进行图像识别图像识别相关的数据分析时，LDA是一个有力的工具。下面总结下LDA算法的优缺点。

LDA算法的主要优点

　　　　1）在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识。

　　　　2）LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。

LDA算法的主要缺点有：

　　　　1）LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。

　　　　2）LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。

　　　　3）LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。

　　　　4）LDA可能过度拟合数据。

PCA和LDA的分析比较

LDA用于降维，和PCA有很多相同，也有很多不同的地方，因此值得好好的比较一下两者的降维异同点。

首先我们看看相同点：

1）两者均可以对数据进行降维。

2）两者在降维时均使用了矩阵特征分解的思想。

3）两者都假设数据符合高斯分布。

我们接着看看不同点：

1）LDA是有监督的降维方法，而PCA是无监督的降维方法

2）LDA降维最多降到类别数k-1的维数，而PCA没有这个限制。

3）LDA除了可以用于降维，还可以用于分类。

4）LDA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向。