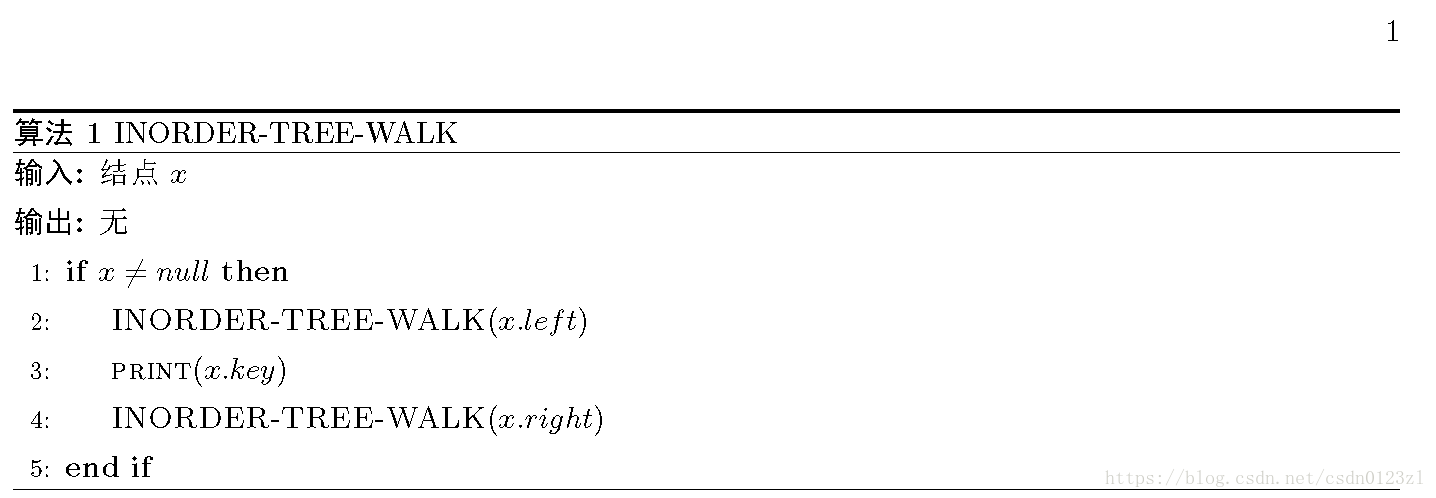《算法导论笔记》——十分钟带你了解二叉搜索树(BST)!
注:本文为《算法导论》中二叉树相关内容的笔记。对此感兴趣的读者还望支持原作者。搜索树数据结构支持许多动态集合操作,包括SEARCH(查找指定结点)、MINIMUM(最小关键字结点)、MAXMUM(最大关键字结点)、PREDECESSOR(结点的先驱)、SUCCESSOR(结点的后继)、INSERT(结点的插入)和DELETE(结点的删除)等。因此,我们使用一棵搜索树既可以作为一个字典又可以作为一个优先队列。
二叉搜索树上的基本操作所花费的时间与这棵树的高度成正比。对于有n个结点的一棵完全二叉树来说,这些操作的最坏运行时间为 Θ ( lg n ) \Theta(\lg n) Θ(lgn)。然而,如果这棵树是一条 n n n个结点组成的线性链,那么同样的操作就要花费 Θ ( n ) \Theta(n) Θ(n)的最坏运行时间。当然,我们可以通过随即构造一棵二叉搜索树的期望高度为 O ( n lg n ) O(n \lg n) O(nlgn),因此这样一棵的动态集合的基本操作的平均运行时间是 Θ ( lg n ) \Theta(\lg n) Θ(lgn)。
基本概念
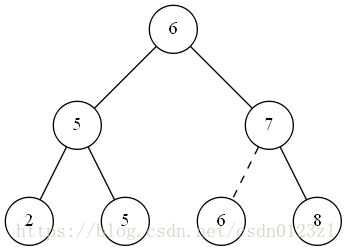
顾名思义,二叉搜索树是一棵二叉树,如图所示。这样一棵树可以使用一个链表结构表示,其中每个结点就是一个对象。除了结点中的关键字外,每个结点还包含属性 l e f t 、 r i g h t 、 p left、right、p left、right、p,它们分别指向结点的左孩子、右孩子和双亲。如果某个孩子结点和父结点不存在,则相应属性的值为 n u l l null null。根结点是树中唯一父结点为 n u l l null null的结点。
二叉搜索树中的关键字总数以满足二叉搜索树性质的方式来存储:设 x x x是二叉搜索树中的一个结点。如果 y y y是 x x x左子树中的一个结点,那么 y . k e y ≤ x . k e y y.key \le x.key y.key≤x.key;如果 y y y是 x x x右子树中的一个结点,那么 y . k e y ≥ x . k e y y.key \ge x.key y.key≥x.key。这一性质,我们从上图中不难看出。树根的关键字为6,在其左子树中右关键字为2,5,它们均不大于6;在其右子树中有关键字7和8,它们均不小于6。这个性质对树中的每个结点都成立。
二叉搜索树的这一性质允许我们通过一个递归算法来按序输出二叉搜索树中的所有关键字。这种算法称为中序遍历。这样命名的原因是输出的子树根的关键字在其左右子树的关键字之间(类似地,先序遍历中的根的关键字在其左右子树的关键字之前,而后序遍历中的根的关键字在其左右子树的关键字之后)。中序遍历的伪代码如下所示。
不难看出,遍历一棵有 n n n个结点的二叉搜索树需要耗费 Θ ( n ) \Theta(n) Θ(n)时间。
查询
我们经常需要查找一个存储在二叉搜索树中的关键字。除了SEARCH操作之外,二叉搜索树还支持MINIMUM、MAXMUM、PREDECESSOR、SUCCESSOR的查询操作。接下来,我们首先看看SEARCH操作是如何实现的。
查找

如图所示,查找过程从树根开始,并沿着这棵树的一条简单路径向下进行。对于遇到的每个结点 x x x,比较关键字 k k k与 x . k e y x.key x.key。如果两个关键字相等或者不存在关键字为 k k k的结点,查找就终止。如果 k k k小于 x . k e y x.key x.key,查找在 x x x的左子树继续,因为二叉搜索树的性质蕴含了 k k k不可能被存储在 x x x的右子树中。对称地,如果 k k k大于 x . k e y x.key x.key,查找在右子树中继续。如此,从树根开始查找,遇到的结点就形成了一条向下的简单路径,所以SEARCH的运行时间为 O ( h ) O(h) O(h),其中 h h h为这棵树的高度。
最大关键字元素和最小关键字元素
通过从树根开始沿着 l e f t left left孩子指针直到遇到一个 n u l l null null,我们总能在一颗二叉搜索树中找到一个元素,如下所示。
二叉搜索树性质保证了MINIMUM过程的正确性。如果结点 x x x没有左子树,那么由于 x x x的右子树中的结点的关键字都不小于 x x x的关键字,则以 x x x为根的子树中的最小关键字元素就是 x x x。如果结点 x x x有左子树,那么由于其右子树中没有关键字小于 x . k e y x.key x.key,且在左子树中的每个关键字不大于 x . k e y x.key x.key,则以 x x x为根的子树中的最小关键字一定在以 x . l e f t x.left x.left为根的子树中。因此, M I N I M U M MINIMUM MINIMUM过程一定能找到以 x x x为根结点的子树的最小元素。同样地,寻求最大关键字元素的过程MAXMUM是对称的。这两个过程在一棵高度为 h h h的树中均能在 O ( h ) O(h) O(h)时间内执行完毕。
后继与先驱
给定一棵二叉搜索树中的一个结点,有时需要按中序遍历的次序查找它的后继。如果所有的关键字互不相同,则一个结点 x x x的后继是大于 x . k e y x.key x.key的最小关键字的结点。一棵二叉搜索树的结构允许我们通过没有任何关键字的比较来确定一个结点的后继。如果后继存在,SUCCESSOR过程将返回一棵二叉搜索树中的结点 x x x的后继;如果 x x x是这棵树中的最大关键字元素,则返回 n u l l null null。SUCCESSOR过程如下。
从上图中不难看出,结点的后继分为两种情况:如果结点 x x x的右子树非空,那么 x x x的后继恰是其右子树的最左结点;如果结点 x x x的右子树为空并有一个后继 y y y,那么 y y y是 x x x的最底层祖先,并且 y y y的左孩子要么是结点 x x x本身,要么也是 x x x的一个祖先。如此,我们便能找到结点 x x x的后继。同样地,PREDECESSOR过程与SUCCESSOR过程是对称地,且它们的运行时间也为 O ( h ) O(h) O(h)。
插入与删除
插入和删除操作会引起二叉搜索树表示的动态集合的变化。一定要修改数据结构来反映这个变化,但修改要保持二叉搜索树性质的成立。接下来,我们将首先看看插入操作。
插入
INSERT示意图如下。
上图中,向二叉搜索树 T T T插入关键字为6的结点。要将一个新值 v v v插入到一棵二叉搜索树 T T T中,需要调用过程INSERT。该过程以结点 z z z作为输入,其中 z . k e y = v , z . l e f t = n u l l , z . r i g h t = n u l l z.key = v, z.left = null, z.right = null z.key=v,z.left=null,z.right=null。这个过程要修改 T T T和 z z z的某些属性,来把 z z z插入到树中的相应位置。过程INSERT如下。
正如SEARCH过程一样,过程INSERT从树根开始,指针 x x x记录了一条向下的简单路径,并查找要替换的输入项 z z z的 n u l l null null。在找到合适的位置后,我们更新 z z z的父结点以及 z z z的父结点的孩子结点信息从而完成INSERT过程。不难看出,INSERT过程在一棵高度为 h h h的树上的运行时间为 O ( h ) O(h) O(h)。
删除
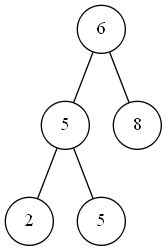
DELETE过程示意图如下。
上图中,关键字为7的结点从二叉搜索树中删除。而一般来说,从一棵二叉搜索树 T T T中删除一个结点 z z z的整个策略分为三种基本情况:
- 如果 z z z没有孩子结点,那么只是简单地将它删除,并修改它的父结点,用 n u l l null null作为孩子来替换 z z z。
- 如果 z z z只有一个孩子结点,那么将这个孩子提升到树中 z z z的位置上,并修改它的父结点,用 z z z的孩子来替换 z z z。
- 如果 z z z有两个孩子结点,那么找 z z z的后继(一定在 z z z的右子树中) y y y,并让 y y y占据树中 z z z的位置。 z z z的原来右子树部分成为 y y y的新的右子树, z z z的原来左子树部分成为 y y y的新的左子树。
而为了完成二叉搜索树中结点的DELETE过程,我们需要定义一个子过程TRANSPLANT,它是用另一棵子树来替换一棵子树并成为其双亲的孩子结点。我们通过此过程来完成上述三种情况中的替换工作。TRANSPLANT过程如下。
通过子过程TRANSPLANT,我们便可以实现DELETE过程。
显然,在一棵高度为 h h h的二叉搜索树中,DELETE过程的运行时间为 O ( h ) O(h) O(h)。
二叉搜索树的实现
好了,二叉搜索树相关概念介绍了这么多,是时候将其付诸实践了!毕竟,“光说不练假把式”!下面给出了二叉搜索树的Java版本。
import java.util.Random;
/**
* 二叉搜索树
* @author 爱学习的程序员
* @version V1.0
*/
public class BST{
// 根结点
public static Node root = null;
/**
* 二叉搜索树的结点类
*/
public static class Node{
// 父结点
Node p;
// 左孩子
Node left;
// 右孩子
Node right;
// 关键字
int key;
public Node(Node p, Node left, Node right, int key){
this.p = p;
this.left = left;
this.right = right;
this.key = key;
}
}
/**
* 插入结点
* @param z 待插入结点
* @return 根结点
*/
public static void insert(Node z){
// 树为空,直接作为根结点
if(root == null)
root = z;
else{
Node y = null;
Node x = root;
// 寻求树中结点z的合适位置
while(x != null){
y = x;
if(z.key < x.key)
x = x.left;
else
x = x.right;
}
z.p = y;
if(z.key < y.key)
y.left = z;
else
y.right = z;
}
}
/**
* 中序遍历二叉搜索树
* @param x 树中结点
* @return 无
*/
public static void inorderTreeWalk(Node x){
if(x!=null){
inorderTreeWalk(x.left);
System.out.print(x.key+"\t");
inorderTreeWalk(x.right);
}
}
/**
* 二叉搜索树中查找一个具有指定关键字的结点
* @param x 树中结点
* @param k 关键字
* @return 无
*/
public static Node search(Node x, int k){
while(x != null && x.key != k){
if(k < x.key)
x = x.left;
else
x = x.right;
}
return x;
}
/**
* 二叉搜索树中关键字最小的结点
* @param x 树中结点
* @return 关键字最小的结点
*/
public static Node minimum(Node x){
while(x.left != null)
x = x.left;
return x;
}
/**
* 二叉搜索树中关键字最大的结点
* @param x 树中结点
* @return 关键字最大的结点
*/
public static Node maxmum(Node x){
while(x.right != null)
x = x.right;
return x;
}
/**
* 结点的后继(中序遍历)
* @param x 树中结点
* @return 结点的后继
*/
public static Node successor(Node x){
// 如果x的右子树不为空,则x的后继为x的右子树中具有最小关键字的结点
if(x.right != null)
return minimum(x.right);
// 如果x的右子树为空,则x的后继为x的最底层祖先,而且它的左孩子也是x的一个祖先(左孩子是x即可)
else{
Node y = x.p;
while(y !=null && x == y.right){
x = y;
y = y.p;
}
return y;
}
}
/**
* 结点的先驱(代码与结点的后继对称)
* @param x 树中结点
* @return 结点的先驱
*/
public static Node predecessor(Node x){
if(x.left != null)
return maxmum(x.left);
else{
Node y = x.p;
while(y !=null && x == y.left){
x = y;
y = y.p;
}
return y;
}
}
/**
* 二叉搜索树内移动子树(用另一棵子树替换一棵子树,并成为其父结点的孩子结点)
* @param u 被替换子树的根结点
* @param v 替换子树的根结点
* @return 无
*/
public static void transplant(Node u, Node v){
if(u.p == null)
root = v;
else if(u == u.p.left)
u.p.left = v;
else
u.p.right = v;
if(v != null)
v.p = u.p;
}
/**
* 删除指定结点
* @param z 待删除结点
* @return 无
*/
public static void delete(Node z){
// 如果z最多有一个孩子结点,则直接调用transplant
if(z.left == null)
transplant(z, z.right);
else if(z.right == null)
transplant(z, z.left);
// 如果z两个孩子结点都存在,则寻找其后继
else{
// z的后继
Node y = minimum(z.right);
if(y.p != z){
transplant(z, z.right);
y.right = z.right;
y.right.p = y;
}
transplant(z, y);
y.left = z.left;
y.left.p = y;
}
}
public static void main(String[] args){
Random rand = new Random();
// 结点数组
Node[] node = new Node[10];
int i = 0;
System.out.println("生成二叉树结点并插入树中:");
for(i = 0; i < node.length ;i++){
node[i] = new Node(null, null, null, rand.nextInt(100) + 1);
System.out.print(node[i].key+"\t");
insert(node[i]);
}
// 中序遍历
System.out.println("\n"+"中序遍历二叉搜索树:");
inorderTreeWalk(root);
// 查找指定结点
Node x = search(root, node[5].key);
System.out.println("\n"+"查找结果:");
System.out.println("自身关键字:"+x.key+"\t"+"父结点的关键字:"+x.p.key);
// 具有最小关键字的结点
x = minimum(root);
System.out.println("树中最小关键字:"+x.key);
// 具有最大关键字的结点
x = maxmum(root);
System.out.println("树中最大关键字:"+x.key);
// x的后继
x = predecessor(node[5]);
System.out.println("前驱的关键字:"+x.key);
// x的前驱
x = successor(node[5]);
System.out.println("后继的关键字:"+x.key);
// 删除结点,并中序输出观看结果
delete(node[5]);
System.out.println("删除结点:");
inorderTreeWalk(root);
}
}
总结
本篇博客介绍了二叉搜索树的概念,及在二叉搜索的一些基本操作。根据二叉搜索树的性质,我们发现诸如SEARCH(查找指定结点)、MINIMUM(最小关键字结点)、MAXMUM(最大关键字结点)、PREDECESSOR(结点的先驱)、SUCCESSOR(结点的后继)、INSERT(结点的插入)和DELETE(结点的删除)等基本操作的时间复杂度为 O ( lg n ) ) O(\lg n)) O(lgn))。这是十分令人满意的。然而,如果这棵树是一条 n n n个结点组成的线性链,那么同样的操作就要花费 Θ ( n ) \Theta(n) Θ(n)的最坏运行时间。因此,为了充分利用二叉搜索树的优点,此后出现了很多二叉搜索树的变形版本,如红黑树等。而下篇博客,我们就将一起探索红黑树的魅力!