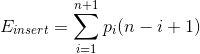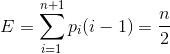线性数据结构——线性表
数据结构
数据结构可以用一个二元组来定义,DataStructure = (D,S)。其中D是数据元素的有限集,S是D上关系的集合。这里的关系代表着数据元素之间的逻辑关系,即逻辑结构,通常指集合、线性表、树、图四种结构。另一方面,某种数据结构在计算机中的具体排列情况又称为物理结构,分为顺序存储结构和链式存储结构。任何逻辑结构都只能由这两种物理结构来实现,选择不同的物理结构得到的性能和优点也各不相同。
线性表
直观的讲线性表就是以一一对应关系排列下去的有限序列。除首位外,每个元素存在唯一的前驱,除末位外,每个元素存在唯一的后继。下面从增删查改这四个主要操作入手,分别讲解顺序存储和链式存储下的线性表。
一、顺序存储线性表
高级语言中的数组符合在内存中连续的特点,通常以其作为实现顺序存储的载体。数组的特点是可以在O(1)时间内读写任意一个位置的数据,而插入和删除操作则需要移动大量的元素,导致时间复杂度增加为O(n)。
增
在长度为n的顺序表的第i个位置前插入一个元素,我们要做的是将第i个以及之后的所有元素整体向后移动一位,可以想象老式手机滑动露出键盘的过程,如图所示。
下面来做一点数学,计算插入操作所需的平均时间。在第i个位置插入元素的概率为![]() ,这之后要移动的元素为n-i+1个,那么插入所需时间的期望值为
,这之后要移动的元素为n-i+1个,那么插入所需时间的期望值为
假设元素插入到每个位置的概率相等,那么![]() (多1是因为可以插入到末尾没有元素的位置),代入后计算得到
(多1是因为可以插入到末尾没有元素的位置),代入后计算得到![]() ,故插入操作得时间复杂度为O(n)。
,故插入操作得时间复杂度为O(n)。
删
删除长度为n的顺序表的第i个位置的元素,操作与插入类似,只不过删除是将第i个之后(不包括第i个)的所有元素都向前移动一位,从而覆盖第i个元素实现删除的效果。
同样,我们计算一下所需时间的期望值,删除的是第i个元素的概率为![]() ,要移动的元素个数为n-i,期望值为
,要移动的元素个数为n-i,期望值为
仍假设删除各个位置的元素的概率相等,![]() ,代入得到
,代入得到![]() ,故删除操作的时间复杂度为O(n)。
,故删除操作的时间复杂度为O(n)。
查
前面已阐述过顺序存储的特点,即可以实现随机访问,故读取任意位置的元素的时间复杂度为O(1)。具体而言,在数组中我们可以通过下标来直接获取某个位置的元素。
改
同理,写入也可以通过随机访问实现,其时间复杂度为O(1)。
二、链式存储线性表
链式存储主要是通过一种包含数据域和指针域的数据结构作为结点链接而成。每个结点除了存储有这个结点表示的数据,还另外存有一个指针用于指向下一个结点(这里仅讨论单向链表)。特别地,我们把第一个结点叫做头结点,并将一个指向它的指针保存下来,作为对链表进行各种操作的线索,称为头指针。链式存储的特点是它在内存空间中是非连续的,要访问任意一个结点只能从头开始,循着指针一路走到这个结点的位置,因此读取和写入的时间复杂度均为O(n)。
增
在长度为n的链表的第i位之前插入一个元素,记第i个结点为this,并构造一个新的结点,称它为new,将要插入的数据赋值到new的数据域。假设我们已经找到this的前一个结点pre(而不需要知道this),那么插入操作可以由以下步骤实现:
(1)将new的指针指向pre当前指向的结点(即this)
(2)修改pre的指针,令其指向new
具体的代码实现可以在网上任意找到参照,这里仅关注其中运用的思想和分析算法性能。显然,上面的步骤总数是固定不变的,与链表长度无关,故在已知前一个结点的情况下,插入操作的时间复杂度为O(1)。
然而一般来讲,我们是无法直接获取到插入位置的前一个结点的,这需要从头结点开始,不断访问下一个结点,直到第i-1个结点,该过程经历了i-1步操作。假设插入在每个位置的概率是相等的,即 ![]() ,由此可知寻找前驱结点的复杂度期望值为
,由此可知寻找前驱结点的复杂度期望值为
即寻找前驱结点时间复杂度为O(n),那么插入过程的总的时间复杂度为O(n)+O(1)=O(n)。
删
删除长度为n的链表中的第i位,我们同样记第i个结点为this,其前驱为pre,在已找到pre的情况下,删除操作如下:
(1)将pre的指针指向this的下一位
(2)删除this结点
上述过程的时间复杂度为O(1),而寻找前驱的时间复杂度为O(n),故删除操作的时间复杂度总共为O(n)。
查
分析读取链表的第i位的复杂度,我们可以借用上面的寻找第i位前驱结点的结论。首先找到第i个结点的前驱用时为O(n),然后仅需一步操作即可找到第i个结点,故其总时间复杂度仍为O(n)。
改
修改第i位的数据与读取类似,都只需找到该结点即可,时间复杂度同样为O(n)。