字符串算法之Manacher（最长回文子串）

一、背景

  在介绍算法之前，首先介绍一下什么是回文串，所谓回文串，简单来说就是正着读和反着读都是一样的字符串，比如abba，noon等等，一个字符串的最长回文子串即为这个字符串的子串中，是回文串的最长的那个。

  计算字符串的最长回文字串最简单的算法就是枚举该字符串的每一个子串，并且判断这个子串是否为回文串，这个算法的时间复杂度为O(n^3)的，显然无法令人满意，稍微优化的一个算法是枚举回文串的中点，这里要分为两种情况，一种是回文串长度是奇数的情况，另一种是回文串长度是偶数的情况，枚举中点再判断是否是回文串，这样能把算法的时间复杂度降为O(n^2)，但是当n比较大的时候仍然无法令人满意，Manacher算法可以在线性时间复杂度内求出一个字符串的最长回文字串，达到了理论上的下界。

二、Manacher算法原理与分析

1、算法分析

  由于回文分为偶回文（比如 bccb）和奇回文（比如 bcacb），而在处理奇偶问题上会比较繁琐，所以这里我们使用一个技巧，具体做法是：在字符串首尾，及各字符间各插入一个字符（前提这个字符未出现在串里）。

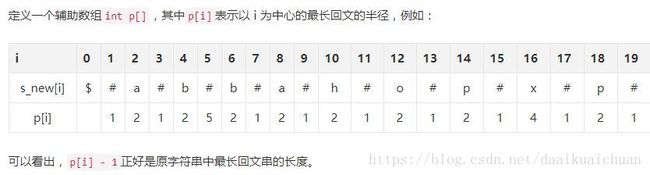
  举个例子：s="abbahopxpo"，转换为s_new="$#a#b#b#a#h#o#p#x#p#o#"（这里的字符 $ 只是为了防止越界，下面代码会有说明），如此，s 里起初有一个偶回文abba和一个奇回文opxpo，被转换为#a#b#b#a#和#o#p#x#p#o#，长度都转换成了奇数。

2、如何求解p数组

如果i点包含在当前最长回文子串之中(肯定要包含，不然求个鬼)，那么i点的回文子串长度为下列两种情况的最小值。

  现在开始分析：

三、Manacher算法的demo

#include 
#include 
#include 
#include 
using namespace std;

string getstr(string &s)
{
    int k = 0;
    const int len = s.size();
    string str;
    str.resize(100);
    str[k++] = '$'; //防止数组越界
    for (int i = 0; i < len; ++i)
    {
        str[k++] = '#';//添加一些字符，使得字符串的长度总是奇数
        str[k++] = s[i];
    }
    str[k++] = '#';
    //删除多余字符
    str.erase(remove(str.begin(), str.end(), '\0'), str.end());
    return str;
}

int Manacher(string &s)
{
    string str_new = getstr(s);//获取新的字符串
    int len = str_new.size();
    vector<int> p;
    p.resize(len);
    int max_len = -1;  //设置初始的最长回文长度
    int id = 0;
    int mx = 0;
    for (int i = 1; i < len; ++i)
    {
        if (i < mx)
        /*
        *1、i关于中心 id 对称的点 j 的已知子串长度（左边对称点 j=2id-i 的最长回文子串长度已知）：
        *
        *因为 i 和 j 是关于 id 的对称点，而 id 子串（以 id 为中心的最长回文子串，下同）
        *肯定是左右对称且包含了 i 子串(前提)，那么 i 子串必定与 j 子串对称，所以可以直接
        *继承已经计算过的 j 的最长子串长度 P[j] ，即 P[i]=P[j]=P[2id-i]
        *
        *2、右边界到 i 点的距离（无论超过边界还是正好处于边界，都取最小值 mx-i ）：
        *
        * 在这种情况下， i 子串并不完全包含在 id 子串中，但是容易看出的是， i子串至少会有 
        * mx-i 的长度（正好达到边界），即 P[i]>=mx-i
        */
            p[i] = min(p[2 * id - i], mx - i);
        else
            p[i] = 1;
        //当前位置的最长回文子串超过mx了，所以向后遍历
        while (str_new[i - p[i]] == str_new[i + p[i]])
            p[i]++;
        // 我们每走一步 i，都要和 mx 比较，我们希望 mx 尽可能的远，这样才能更有机会执行 
        // if (i < mx)这句代码，从而提高效率
        if (mx < i + p[i])
        {
            mx = i + p[i];
            id = i;
        }
        //最长回文子串就是p[i] - 1
        max_len = max(max_len, p[i] - 1);
    }
    return max_len;
}

int main(int argc, char const *argv[])
{
    string str;
    getline(cin, str);
    cout << Manacher(str);
    return 0;
}

  Manacher算法的时间复杂度为O(n)。

转自：https://segmentfault.com/a/1190000008484167
https://www.zhihu.com/question/37289584