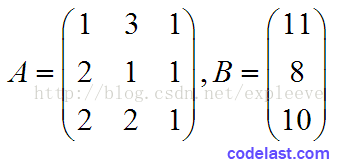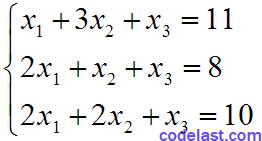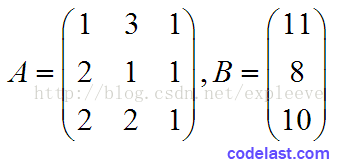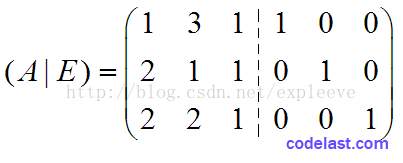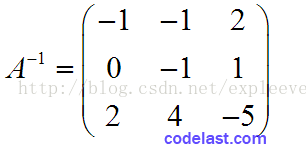高斯-约当(Gauss-Jordan)消元法
选主元的高斯-约当(Gauss-Jordan)消元法在很多地方都会用到,例如求一个矩阵的逆矩阵、解线性方程组(插一句:LM算法求解的一个步骤),等等。它的速度不是最快的,但是它非常稳定(来自网上的定义:一个计算方法,如果在使用此方法的计算过程中,舍入误差得到控制,对计算结果影响较小,称此方法为数值稳定的),同时它的求解过程也比较清晰明了,因而人们使用较多。下面我就用一个例子来告诉你Gauss-Jordan法的求解过程吧。顺便再提及一些注意事项以及扩展话题。
对本文中所提到的“主元”等概念的解释,可以参考此链接。
假设有如下的方程组:
写成矩阵形式就是:AX=B,其中:
且X=(X1, X2, X3)T。
文章来源:http://www.codelast.com/
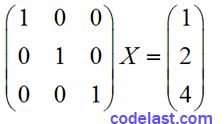
现对矩阵A作初等变换,同时矩阵B也作同样的初等变换,则当A化为单位矩阵的时候,有:
显而易见,我们得到了方程组的解X=(1, 2, 4)T。
所以,我们要以一定的策略,对A和B施以一系列的初等变换,当A化为单位矩阵的时候,B就为方程组的解。
选主元的G-J消元法通过这样的方法来进行初等变换:在每一个循环过程中,先寻找到主元,并将主元通过行变换(无需列变换)移动到矩阵的主对角线上,然后将主元所在的行内的所有元素除以主元,使得主元化为1;然后观察主元所在的列上的其他元素,将它们所在的行减去主元所在的行乘以一定的倍数,使得主元所在的列内、除主元外的其他元素化为0,这样就使得主元所在的列化为了单位矩阵的形式。这就是一个循环内做的工作。然后,在第二轮循环的过程中,不考虑上一轮计算过程中主元所在的行和列内的元素,在剩下的矩阵范围内寻找主元,然后(如果其不在主对角线上的话)将其移动到主对角线上,并再次进行列的处理,将列化为单位矩阵的形式。余下的步骤依此类推。具体的计算过程的一个例子,请看下面我举的求逆矩阵的过程。
如果要解系数矩阵相同、右端向量不同的N个方程组,在设计程序的时候,没有必要”解N次方程组“,我们完全可以在程序中,将所有的右端向量以矩阵的数据结构(类似于二维数组)来表示,在系数矩阵作行变换的时候,矩阵里的每一个右端向量也做同样的变换,这样,我们在一次求解运算的过程中,实际上就是同时在解N个方程组了,这是要注意的地方。
文章来源:http://www.codelast.com/
那么,G-J法为什么可以用来求逆矩阵?
假设AX=E,其中,A为n阶系数矩阵(与上面的解线性方程组对照);E为单位矩阵,即E=(e1,e2,…,en),其中ei (i=1,2,…,n) 为单位列向量;X为n个列向量构成的矩阵,即X=(x1,x2,…,xn),其中xi (i=1,2,…,n) 为列向量。于是,可以把等式AX=E看成是求解n个线性方程组Axi=ei (i=1,2,…,n),求出了所有的xi之后,也即得到了矩阵X。而由AX=E可知,矩阵X是A的逆矩阵,即X=A-1。这样,就求出了A的逆矩阵了。于是,求逆矩阵的过程被化成了解线性方程组的过程,因此我们可以用Gauss-Jordan消元法来求逆矩阵。
求逆矩阵时,系数矩阵A和单位矩阵E可以共用一块存储区,在每一次约化过程中,系数矩阵逐渐被其逆矩阵替代。
在这里,我用一个实际的例子来说明G-J法求逆矩阵的过程:
有如下的方程组:
显而易见,该方程组对应的系数矩阵A和右端向量矩阵B(此处只有一个右端向量)分别为:
其实在求逆矩阵的过程中,矩阵B无关紧要,可以忽略,不过此处还是把它写出来了。下面,把单位矩阵E附在A的右边,构成另一个矩阵(A|E):
文章来源:http://www.codelast.com/
下面,我们就通过矩阵的初等变换,将A化为单位矩阵E,而E则化为了A的逆矩阵。以下是转化步骤:
- 【Step 01】主元选为3,所以将Row1(第一行)与Row2(第二行)交换:
- 【Step 02】主元所在行的所有元素除以主元:
- 【Step 03】Row1 - Row2,Row3 - 2 × Row2:
现在,原来的矩阵A有一列被化为了单位阵的形式。
- 【Step 04】重新选主元,这一次主元选为5/3,于是Row1 ÷ 5/3(主元所在行的所有元素除以主元):
- 【Step 05】Row2 - (1/3) × Row1,Row3 - (4/3) × Row1:
现在,原来的矩阵A又有一列被化为了单位阵的形式。
- 【Step 06】重新选主元,这一次主元选为-1/5,于是Row3 ÷ (-1/5)(主元所在行的所有元素除以主元):
- 【Step 07】Row1 - (2/5) × Row3,Row2 - (1/5) × Row3:
现在,原来的矩阵A的所有列都被化为了单位阵的形式。
可见,以上过程非常适合于计算机编程求解。
文章来源:http://www.codelast.com/
至此,我们完成了从A到E的转换,这个过程中使用了选主元的方法,但没有使用列交换。于是,原来的单位矩阵E就变成了A-1,即:
有人说,在进行转化的过程中,如果某一步发现选中的主元为0,怎么办?当然,这种情况就进行不下去了(矩阵是奇异的)。
来源:http://www.codelast.com/?p=1288