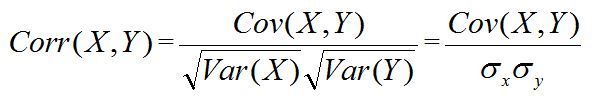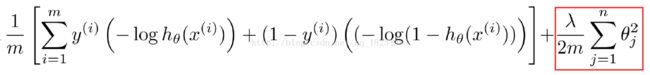【过拟合和欠拟合】【Lasso算法】

1、过拟合

所谓过拟合（over-fitting）其实就是所建的机器学习模型或者是深度学习模型在训练样本中表现得过于优越，导致在验证数据集以及测试数据集中表现不佳。打个比喻就是当我需要建立好一个模型之后，比如是识别一只狗狗的模型，我需要对这个模型进行训练。恰好，我训练样本中的所有训练图片都是二哈，那么经过多次迭代训练之后，模型训练好了，并且在训练集中表现得很好。基本上二哈身上的所有特点都涵括进去，那么问题来了！假如我的测试样本是一只金毛呢？将一只金毛的测试样本放进这个识别狗狗的模型中，很有可能模型最后输出的结果就是金毛不是一条狗（因为这个模型基本上是按照二哈的特征去打造的）。所以这样就造成了模型过拟合，虽然在训练集上表现得很好，但是在测试集中表现得恰好相反，在性能的角度上讲就是协方差过大（variance is large），同样在测试集上的损失函数（cost function）会表现得很大。

1.1协方差

协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。

协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

二维随机变量（X，Y），X与Y之间的协方差定义为：

Cov(X,Y)=E{[X-E(X)][Y-E(Y)]}

其中：E(X)为分量X的期望，E(Y)为分量Y的期望

它是X的偏差【X-E(X)】与Y的偏差【Y-E(Y)】的乘积的数学期望

1.1.1相关系数

相关系数的定义，范围在【-1，1】

 

其中：Var(X)为X的方差，Var(Y)为Y的方差，其中Var(X)和Var(Y)叫做正则化因子，

1.1.2协方差为0和独立

Corr(X,Y)为0，表示X与Y不相关，这里的不相关指的是X与Y没有线性关系，但不是没有关系。因此将“相关”理解为“线性相关”也许更恰当一些

2、欠拟合

所谓欠拟合呢（under-fitting）？相对过拟合欠拟合还是比较容易理解。还是拿刚才的模型来说，可能二哈被提取的特征比较少，导致训练出来的模型不能很好地匹配，表现得很差，甚至二哈都无法识别。

3、正则化平衡欠拟合和过拟合

使得cost function始终不为0，这样就可以

回想下我们的模型，假如我们采用梯度下降算法将模型中的损失函数不断减少，那么最终我们会在一定范围内求出最优解，最后损失函数不断趋近0。那么我们可以在所定义的损失函数后面加入一项永不为0的部分，那么最后经过不断优化损失函数还是会存在。其实这就是所谓的“正则化”。

下面这张图片就是加入了正则化（regulation）之后的损失函数。这里m是样本数目，landa（后面我用“t”表示，实在是打不出）表示的是正则化系数。

注意：当t（landa）过大时，则会导致后面部分权重比加大，那么最终损失函数过大，从而导致欠拟合

   当t（landa）过小时，甚至为0，导致过拟合。

4、减少神经网络规模（深度）的方法减少过拟合

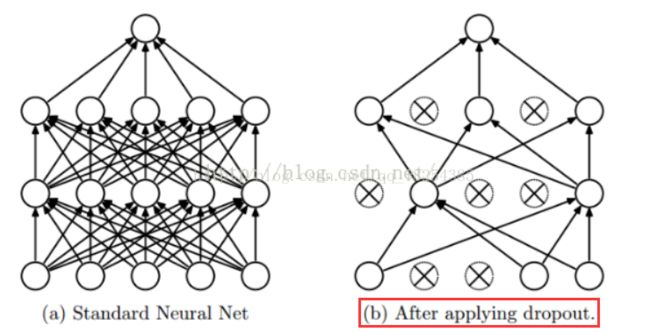
对于神经网络，参数膨胀原因可能是因为随着网路深度的增加，同时参数也不断增加，并且增加速度、规模都很大。那么可以采取减少神经网络规模（深度）的方法。也可以用一种叫dropout的方法。dropout的思想是当一组参数经过某一层神经元的时候，去掉这一层上的一部分神经元，让参数只经过一部分神经元进行计算。注意这里的去掉并不是真正意义上的去除，只是让参数不经过一部分神经元计算而已。

5、平衡欠拟合和过拟合其余方法

增大训练样本解决过拟合

欠拟合：

其实个人觉得欠拟合基本上都会发生在训练刚开始的时候，经过不断训练之后欠拟合应该不怎么考虑了。。但是如果真的还是存在的话，可以通过增加网络复杂度或者在模型中增加多点特征点，这些都是很好解决欠拟合的方法

6、方差&均方差（标准差）

方差公式如下：

（variance)是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是各个数据分别与其平均数之差的平方的和的平均数。在许多实际问题中，研究方差即偏离程度有着重要意义

均方差就是标准差

7、Ridge脊回归

ridge回归是在一般线性回归的基础上加上L2的正则化项

线性回归问题

Ridge回归问题

由于直接套用线性回归可能产生过拟合，我们需要加入正则化项，如果加入的是L2正则化项，就是Ridge回归，有时也翻译为脊回归。它和一般线性回归的区别是在损失函数上增加了一个L2正则化的项，和一个调节线性回归项和正则化项权重的系数αα。损失函数表达式如下：

Ridge回归在不抛弃任何一个变量的情况下，缩小了回归系数，使得模型相对而言比较的稳定，但这会使得模型的变量特别多，模型解释性差。有没有折中一点的办法呢？即又可以防止过拟合，同时克服Ridge回归

模型变量多的缺点呢？有，这就是下面说的Lasso回归。

8、Lasso算法

Lasso回归有时也叫做线性回归的L1正则化，和Ridge回归的主要区别就是在正则化项，Ridge回归用的是L2正则化，而Lasso回归用的是L1正则化。Lasso回归的损失函数表达式如下：　

其中n为样本个数，αα为常数系数，需要进行调优。||θ||1||θ||1为L1范数。　　　

　　　　Lasso回归使得一些系数变小，甚至还是一些绝对值较小的系数直接变为0，因此特别适用于参数数目缩减与参数的选择，因而用来估计稀疏参数的线性模型。

　　　　但是Lasso回归有一个很大的问题，导致我们需要把它单独拎出来讲，就是它的损失函数不是连续可导的，由于L1范数用的是绝对值之和，导致损失函数有不可导的点。也就是说，我们的最小二乘法，梯度下降法，牛顿法与拟牛顿法对它统统失效了。那我们怎么才能求有这个L1范数的损失函数极小值呢？

　　　　OK，本章主角，两种全新的求极值解法坐标轴下降法（coordinate descent）和最小角回归法（ Least Angle Regression， LARS）该隆重出场了。　

8.1坐标下降法

8.2最小角求lasso回归

第四节介绍了坐标轴下降法求解Lasso回归的方法，此处再介绍另一种常用方法， 最小角回归法(Least Angle Regression， LARS)。

在介绍最小角回归前，我们先看看两个预备算法，好吧，这个算法真没有那么好讲。

8.2.1前向选择算法

8.2.2前向梯度（Forward Stagewise）算法

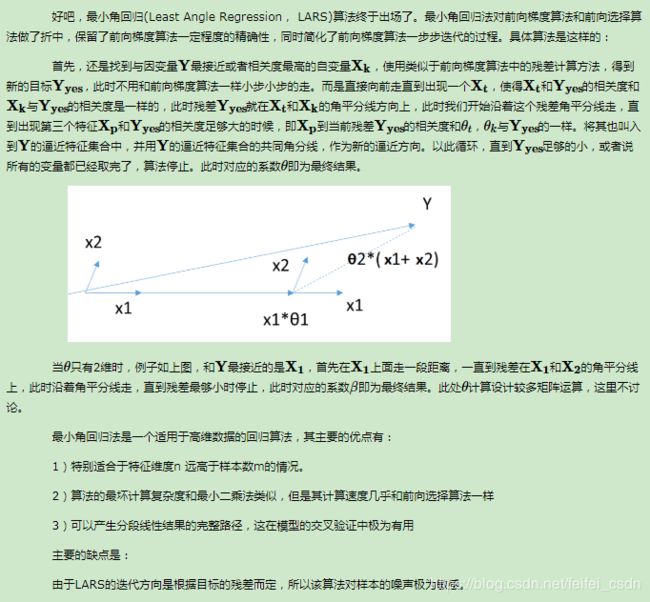
8.2.3 最小角回归(Least Angle Regression， LARS)算法

Lasso回归是在ridge回归的基础上发展起来的，如果模型的特征非常多，需要压缩，那么Lasso回归是很好的选择。一般的情况下，普通的线性回归模型就够了