混淆矩阵、分类评价指标

混淆矩阵

 

混淆矩阵基本上就是上表的表示，展示出实际的类别和分类后的得到的结果。（在目标识别中如何表现出背景那一类？）

抽象出来就是下面的列表：

从TP，TN、FN、FP 可以得到几种指标：

 

1）查准率：

也可以理解为（正样本的）准确率，P = TP/（TP+FP）。在目标识别中就是：检测到正确的目标数目/检测到的目标数目；

上述的查准率公式也有不妥的地方，对于只有一种类别的数据还是不多的，对于两种以上的数据，计算准确率的过程中需要中和考虑所有类别。例如二分类：

ACC = （TP + TN）/ (TP + FP + TN + FN)

对于多分类：

ACC = （TP_c0 + TP_c1 + TP_c2 ...）/ numbers of all target.

 

2）查全率：

也称作 Recall = TP/（TP+FN）。很多任务都需要关注这个值，尤其是医学图像中，例如病灶识别等，重点在于不能漏。

3）F-Score：

对于同时需要关注准确率和召回率的任务就需要将两者结合，f-score就是常见的两者兼顾的指标。具体公式如下：

当 β = 1 时，得到 F1-Score，此时precision和recall权重相等。

 

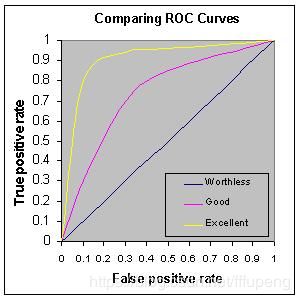
4）ROC（受试者工作特征曲线）

重点：1、二分类 2、不同的判断标准；

对于常见的二分类任务，需要设置中间的阈值，概率大于阈值则为正，小于阈值的则为负。不同的阈值大小会得到不同的判别结果，recall 和acc也受影响。

ROC 能够摆脱阈值对评价结果的影响，单纯地去测试模型的好坏。

步骤：

1、将测试数据按照逻辑回归的大小从大到小进行排序；

2、分别取10%，20%，30% ...100%的样本，将其视为正样本，剩下的负样本，计算敏感度（正样本的查准率）和特异度（负样本的查准度）；

3、按照横坐标为特异度，纵坐标为敏感度绘制曲线，就得到了ROC曲线，如下图所示。

注：ROC曲线受正负样本数量比例的影响！因此在比较ROC曲线的时候注意样本分布。

此处所讲二分类任务并不是猫狗分类这种，而是单纯地将目标和背景分类的任务。

对于多分类任务，对于每个类别都应该有一个ROC曲线。

 

 

5）AUC

AUC就是 ROC曲线下方的面积，通常来讲，由于正样本更加应该受到关注，因此敏感度应该大于特异度，也就是对于曲线上的点，纵坐标应该不小于横坐标。所以一般情况下AUC >=0.5；如果模型完美，AUC = 1；如果模型是随机猜测，AUC = 0.5。