java操作二叉树:构建二叉树;前序、中序、后续、层次遍历
文章目录
- 概念
- 二叉树
- 二叉堆
- 堆的存储
- 堆排序
- java构建二叉树以及前序遍历、中序遍历、后序遍历
概念
二叉树
在计算机科学中,二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。二叉树的第i层至多有2{i-1}个结点;深度为k的二叉树至多有2k-1个结点。
满二叉树: 一棵深度为k,且有2^k-1个节点称之为满二叉树。也就是除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
完全二叉树: 深度为k,有n个节点的二叉树,当且仅当其每一个节点都与深度为k的满二叉树中,序号为1至n的节点对应时,称之为完全二叉树
平衡二叉树: 平衡二叉树又被称为AVL树(区别于AVL算法),它是一棵二叉排序树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。[
二叉排序树:
二叉排序树又叫二叉查找树或者二叉搜索树,它首先是一个二叉树,而且必须满足下面的条件:
- 若左子树不空,则左子树上所有结点的值均小于它的根节点的值;
- 若右子树不空,则右子树上所有结点的值均大于它的根结点的值
- 左、右子树也分别为二叉排序树
- 没有键值相等的节点(?可能是因为不好处理键值相等的节点到底是左节点还是右节点吧)
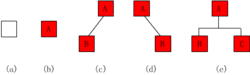
上图中:a: 空二叉树;b:只有一个根结点的二叉树;c:只有左子树;d:只有右子树;e:完全二叉树
二叉树性质
(1) 在非空二叉树中,第i层的结点总数不超过 , i>=1;
(2) 深度为h的二叉树最多有 个结点(h>=1),最少有h个结点;
(3) 对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1;
(4) 具有n个结点的完全二叉树的深度为
(5)有N个结点的完全二叉树各结点如果用顺序方式存储,则结点之间有如下关系:
若I为结点编号则 如果I>1,则其父结点的编号为I/2;
如果2I<=N,则其左儿子(即左子树的根结点)的编号为2I;若2I>N,则无左儿子;
如果2I+1<=N,则其右儿子的结点编号为2I+1;若2I+1>N,则无右儿子。
(6)给定N个节点,能构成h(N)种不同的二叉树。
h(N)为卡特兰数的第N项。h(n)=C(2*n,n)/(n+1)。
(7)设有i个枝点,I为所有枝点的道路长度总和,J为叶的道路长度总和J=I+2i[4]
二叉堆
二叉堆 是一种特殊的堆,二叉堆是完全二元树(二叉树)或者是近似完全二元树(二叉树)。二叉堆有两种:最大堆和最小堆。最大堆 :父结点的键值总是大于或等于任何一个子节点的键值;最小堆:父结点的键值总是小于或等于任何一个子节点的键值。

堆的存储
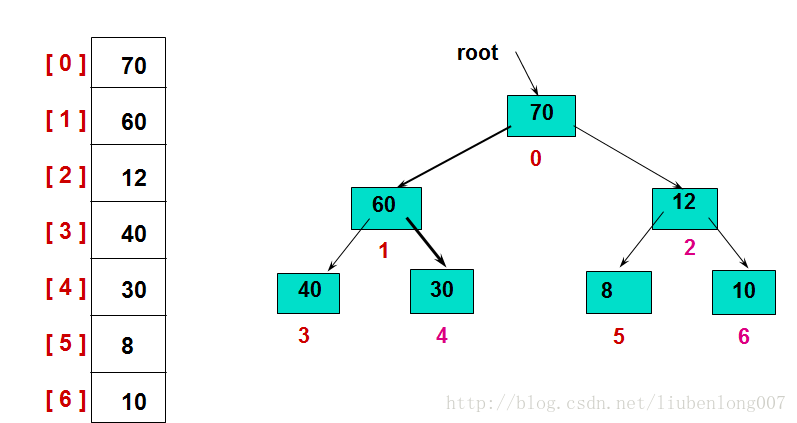
一般用数组来表示堆,若根结点存在序号0处, i结点的父结点下标就为(i-1)/2。i结点的左右子结点下标分别为2i+1和2i+2。如第0个结点左右子结点下标分别为1和2。
堆排序
请参考博主的另一篇文章 java排序算法汇总
接下来我们将对简单的二叉树进行操作。
java构建二叉树以及前序遍历、中序遍历、后序遍历
import lombok.AllArgsConstructor;
import lombok.Builder;
import lombok.Data;
import lombok.NoArgsConstructor;
import java.util.Stack;
/**
* Created by liubenlong on 2017/2/10.
* 二叉树
*/
public class BinaryTree {
/**
* root节点
*/
private Node root = null;
/**
* 二叉树节点数据结构
*/
@Data
@Builder
@AllArgsConstructor
@NoArgsConstructor
private static class Node{
private int data;
private Node leftNode;
private Node rightNode;
}
/**
* 构建二叉排序树
* @param data
*/
public void insert(int data){
root = insert(root, data);
}
public Node insert(Node node, int data){
if(node == null) node = new Node(data, null, null);
else {
if(data > node.getData()) node.setRightNode(insert(node.getRightNode(), data)) ;
else node.setLeftNode(insert(node.getLeftNode(), data));
}
return node;
}
/**
* 先序遍历-递归
*/
public static void preOrderTraverse(Node node){
if(node != null){
System.out.print(node.getData() + ", ");
preOrderTraverse(node.getLeftNode());
preOrderTraverse(node.getRightNode());
}
}
/**
* 中序遍历-递归
* @param node
*/
public static void inOrderTraverse(Node node){
if(node != null){
inOrderTraverse(node.getLeftNode());
System.out.print(node.getData() + ", ");
inOrderTraverse(node.getRightNode());
}
}
/**
* 后续遍历-递归
*/
public static void postOrderTraverse(Node node){
if(node != null){
postOrderTraverse(node.getLeftNode());
postOrderTraverse(node.getRightNode());
System.out.print(node.getData() + ", ");
}
}
/**
* 先序遍历-非递归
* 思路和递归一样,只是这里将递归使用的栈显示的记录而已
*/
public static void preOrderTraverse1(Node node){
Stack<Node> stack = new Stack<>();
if(node != null) stack.add(node);
while(!stack.empty()){
Node nodeTemp = stack.pop();
System.out.print(nodeTemp.getData() + ", ");
if(nodeTemp.getRightNode()!= null) stack.add(nodeTemp.getRightNode());
if(nodeTemp.getLeftNode()!=null) stack.add(nodeTemp.getLeftNode());
}
}
/**
* 中序遍历-非递归
* @param node
*/
public static void inOrderTraverse1(Node node){
Stack<Node> stack = new Stack<>();
if(node != null) stack.add(node);
while(!stack.empty()){
while(node.getLeftNode()!= null) {
stack.add(node.getLeftNode());
node = node.getLeftNode();
}
Node nodeTemp = stack.pop();
System.out.print(nodeTemp.getData() + ", ");
if(nodeTemp.getRightNode() != null) {
stack.add(nodeTemp.getRightNode());
node = nodeTemp.getRightNode();
}
}
}
//层次遍历。比较简答,一个队列搞定
public static void LevelOrder(Node node){
Queue<Node> queue = new ArrayDeque<>();
queue.add(node);
while(!queue.isEmpty()){
Node poll = queue.poll();
System.out.print(poll.getData() + ", ");
if(poll.getLeftNode()!=null)queue.add(poll.getLeftNode());
if(poll.getRightNode()!=null)queue.add(poll.getRightNode());
}
}
/**
* 后续遍历-非递归
* 这个麻烦一点
*/
public static void postOrderTraverse1(Node node){
Node lastPrintNode = node;
Stack<Node> stack = new Stack<>();
while (node != null) {
// 左子树入栈
for (; node.getLeftNode() != null; node = node.getLeftNode())
stack.push(node);
// 当前节点无右子或右子已经输出
while (node != null && (node.getRightNode() == null || node.getRightNode() == lastPrintNode)) {
System.out.print(node.getData() + ", ");
lastPrintNode = node;// 记录上一个已输出节点
if (stack.empty())
return;
node = stack.pop();
}
// 处理右子
stack.push(node);
node = node.getRightNode();
}
}
//计算深度--递归,依次计算其左右子树的深度,选其大者
public static int deep(Node node){
if(node == null) return 0;
//不为空则初始化深度为1
int leftDeep = 1, rightDeep = 1;
if(node.getLeftNode() != null) leftDeep += deep(node.getLeftNode());
if(node.getRightNode() != null) rightDeep += deep(node.getRightNode());
return leftDeep > rightDeep ? leftDeep : rightDeep;
}
/**
* 计算深度(第二种写法)
*/
public static int deep1(Node node) {
if (node != null) {
int i, j;
return 1 + ((i = deep(node.getLeftNode())) > (j = deep(node.getRightNode())) ? i : j);
} else {
return 0;
}
}
public static void main(String[] args){
/**
* 构建二叉树
*/
BinaryTree tree = new BinaryTree();
tree.insert(3);
tree.insert(6);
tree.insert(1);
tree.insert(2);
tree.insert(9);
tree.insert(8);
tree.insert(10);
tree.preOrderTraverse(tree.root);
System.out.println();
tree.inOrderTraverse(tree.root);
System.out.println();
tree.postOrderTraverse(tree.root);
System.out.println();
System.out.println();
preOrderTraverse1(tree.root);
System.out.println();
inOrderTraverse1(tree.root);
System.out.println();
postOrderTraverse1(tree.root);
//层次遍历
System.out.println();
LevelOrder(tree.root);
System.out.println();
int deep = deep(tree.root);
System.out.println("该二叉树的深度为:"+deep);
deep = deep1(tree.root);
System.out.println("【1】该二叉树的深度为:"+deep);
}
}
输出结果
3, 1, 2, 6, 9, 8, 10,
1, 2, 3, 6, 8, 9, 10,
2, 1, 8, 10, 9, 6, 3,
3, 1, 2, 6, 9, 8, 10,
1, 2, 3, 6, 8, 9, 10,
2, 1, 8, 10, 9, 6, 3,
3, 1, 6, 2, 9, 8, 10,
该二叉树的深度为:4