深度学习基础 - 导数
深度学习基础 - 导数
邵盛松
斜率 (图片来自wiki)
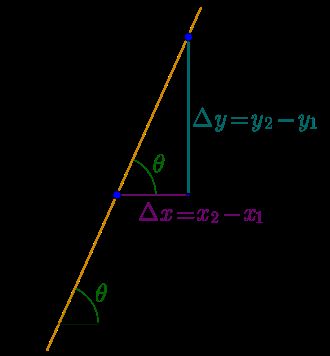
k = tan θ = y 2 − y 1 x 2 − x 1 = Δ y Δ x k = \tan \theta = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } } = \frac { \Delta y } { \Delta x } k=tanθ=x2−x1y2−y1=ΔxΔy
导数
在3Blue1Brown的《微积分的本质 - 02 - 导数的悖论》详细介绍了导数的意义
说明了发明微积分的先辈们为什么要引入一个导数的定义
巴罗、 牛顿 、莱布尼茨发明了微积分,柯西、魏尔斯特拉斯给出了严格定义,
微积分的大厦不是一蹴而就完成的.
牛顿要解决是物理问题,数学是他的工具,如果没有工具,他就自己造。
给行驶中的车辆拍个照,问照片中的这辆车瞬时速度是多少?计算速度 要求路程 和时间,照片中的车没路程没时间哪里来的速度。
速度到底说的是什么意思,
用一小段时间内距离的变化表示,这个很小的时间段,不管有多小,总要有那么个时间段,时间段为 d t dt dt可以想象成0.0000001,只能用逻辑推理,而无法想象有无数个0后面跟着一个1是个什么样的,就像假设宇宙有无限大,无限大怎么想象。 d t dt dt非常非常小的趋近于0, 距离变化为 d s ds ds, 速度 v ( t ) v(t) v(t)就是
d s d t = s ( t + d t ) − s ( t ) d t \frac{ds}{dt}=\frac{s(t+dt)-s(t)}{dt} dtds=dts(t+dt)−s(t)
上述的这个式子就可以描述一个变化率。
d t dt dt这么小是多小,无穷小,那无穷小是多小?
物理上有一个普朗克时间(Planck time)和普朗克长度(Planck length)
按照现有的物理定律来说,我们在理论上也无法推测小于这个长度和时间的东西。
普朗克时间
1 t P ≈ 5.39116 ( 13 ) × 1 0 − 44 s 1 t_{\mathrm{P}} \approx 5.39116(13) \times 10^{-44} \mathrm{s} 1tP≈5.39116(13)×10−44s
普朗克长度
1 ℓ P ≈ 1.616229 ( 38 ) × 1 0 − 35 m 1 \ell_{\mathrm{P}} \approx 1.616229(38) \times 10^{-35} \mathrm{m} 1ℓP≈1.616229(38)×10−35m
无穷小比它还小。
让dt非常接近0,是个技巧,我看这就是萌芽状态的微积分,看这个式子是不是和定义的极限很像,所以定义导数时,先定义了极限。也是因为这个技巧变化率就有了意义
导数就是计算“最佳近似”的工具,就像画一个切线,两点确定一条直线,如果是两个点就是割线。如果是一个点,直线怎么画?还是大牛们想出的那个技巧“无限接近”,
一个点向另一个点不断的移动,两点间的距离越来越近,直线的斜率越来越接近要找的斜率,两点重合为一点,则通过该点的切线的斜率是
= lim h → 0 f ( x + h ) − f ( x ) h = \lim _ { h \rightarrow 0 } \frac { f ( x + h ) - f ( x ) } { h } =h→0limhf(x+h)−f(x)
当极限存在,经过计算得出来的数就成了导数
看割线与切线,图片来自wiki


我主要是做工程,牛人们是发明公式,而我主要是使用着牛人们发明的公式。

f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = lim Δ x → 0 Δ y Δ x f ^ { \prime } ( x ) = \lim _ { \Delta x \rightarrow 0 } \frac { f ( x + \Delta x ) - f ( x ) } { \Delta x } = \lim _ { \Delta x \rightarrow 0 } \frac { \Delta y } { \Delta x } f′(x)=Δx→0limΔxf(x+Δx)−f(x)=Δx→0limΔxΔy
林群在上海交大报告《微积分降到最低点》中举了一个很简单的例子说明什么是导数
微积分之首是导数,擒贼先擒王。导数是什么?
先看整数除法
91 10 = 9 + 0.1 \frac { 91 } { 10 } = 9 + 0.1 1091=9+0.1
若四舍五入,右边剩下整数9,简化做了除法,回到 x 2 x^2 x2
它的导数就是做除法
( x + h ) 2 − x 2 h = ? \frac { ( x + h ) ^ { 2 } - x ^ { 2 } } { h } = ? h(x+h)2−x2=?
简单代数即得等式:对于给定 x x x与任一 h h h
( x + h ) 2 − x 2 h = 2 x + h \frac { ( x + h ) ^ { 2 } - x ^ { 2 } } { h } = 2 x + h h(x+h)2−x2=2x+h
这等式是纯代数,无论 h h h有多大。当你要求 h → 0 h \rightarrow 0 h→0(瞬时速度 ),左边变成除法,但右边变成 2 x + 0 2x+0 2x+0.称为 x 2 x^2 x2的导数,记
( x 2 ) ′ = 2 x \left( x ^ { 2 } \right) ^ { \prime } = 2 x (x2)′=2x
总结他的理解方式是 导数是差商的简化
无穷小量怎么描述?
1 、很小很小量?最小可以小到多少呢?
2 、和0无比接近的量叫做无穷小量?
3 、无穷小量大于0,小于任意正实数的数?
4、是0.000…1(中间有无数个0)吗
被忽略的时期,那么小忽略不计吧。
公元前5世纪的,雅典的,安提芬(Antiphon)创立穷竭法,他在研究“化圆为方”问题时,提出了使用圆内接正多边形面积“穷竭”圆面积的思想。
欧多克斯加以改进并且还给了定义:在一个量中减去比其一半还大的量,不断重复这个过程,可以使剩下的量变得任意小。
阿基米德进一步完善了穷竭法,并将其广泛应用于求解曲面面积和旋转体体积。
卡瓦列里(1598-1647)
重新发明了祖暅原理,刘徽提出后南北朝的祖冲之的儿子祖暅提出。
他们都绕开了无穷小的问题
变成一个刺头的时候,这可是引发第二次数学危机的问题
1734年,英国著名的唯心主义哲学家贝克莱主教(Bishop George Berkeley,1685~1753)发现了一个问题
贝克莱说你看这个式子,你要计算 y = f ( x ) = x 2 y=f(x)=x^{2} y=f(x)=x2的导数
Δ y Δ x = f ( x + Δ x ) − f ( x ) Δ x = ( x + Δ x ) 2 − x 2 Δ x = x 2 + 2 x ∙ Δ x + ( Δ x ) 2 − x 2 Δ x = 2 x + Δ x \begin{aligned} \frac{\Delta y}{\Delta x} &=\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{(x+\Delta x)^{2}-x^{2}}{\Delta x} \\ &=\frac{x^{2}+2 x \bullet \Delta x+(\Delta x)^{2}-x^{2}}{\Delta x} \\ &=2 x+\Delta x \end{aligned} ΔxΔy=Δxf(x+Δx)−f(x)=Δx(x+Δx)2−x2=Δxx2+2x∙Δx+(Δx)2−x2=2x+Δx
牛顿你的无穷小量 Δ x \Delta x Δx先不是0,最后哪一步 Δ x = 0 \Delta x=0 Δx=0,求得导数为 2 x 2x 2x。
大主教贝克莱说你这个无穷小一会儿是0一会儿不是0,我已经被你们数学家绕晕了,我已经懵了,你们没说法,那我就叫它幽灵。你牛顿和莱布尼茨解释解释,你们弄啥嘞?这个bug你怎么修复。
以渺小的哲学家之名出版了一本书,标题很长,不一般的长,题目是《分析学家;或一篇致一位不信神数学家的论文,其中审查一下近代分析学的对象、原则及论断是不是比宗教的神秘、信仰的要点有更清晰的表达,或更明显的推理》。
沃利斯(J. Wallis)
1616-1703 他对极限的定义“含有正确的想法,但用词不严谨”。
莱布尼兹 1646-1716
莱布尼兹说:我来解释解释大主教的问题。
1)它比0大同时比任何实数都小的一个量,
2)它能当除数,在需要的时候可以舍去
3)它是一个消失中的量
达朗贝尔(1717-1783) 和拉格朗日(1736-1813)他俩对莱布尼兹说这不对啊哥们!你拿它来做运算了那它就是个数吧,那是个数就能表示出来吧。它比0大比任何实数都小,这样的数你让二郎神的第三只眼帮你找个让我瞧瞧。
结论是其演算法很成功,但“对概念不太确定”。他对于“消失中的量”的立场是复杂的,而且随时间而变。
那牛顿是如何回答大主教贝克莱的?牛顿说:你说啥,我听不见。
因为牛顿虽然曾试图通过完善自己的理论来解决,但都没有获得完全成功。这使数学家们陷入了尴尬境地:一方面微积分确实可以解决很多问题,另一方面其自身却存在着逻辑矛盾,即“贝克莱悖论”。这一问题的提出在当时的数学界引起了一定的混乱。
贝克莱主教的问题在思想上和方法上深刻影响了近代数学的发展,由此导致了第二次数学危机的产生。
达朗贝尔 说:我给极限的定义,但是说的还不太好。
拉格朗日 说:微积分是代数问题吧。
欧拉 1707-1783
获得了很多重要结果,但不考虑真正无穷小量带来的困难。其观点受十七世纪典型的科学思维框架影响。
总算逻辑自洽了
柯西 1789-1857
其写下的定义至今依然通用,由当时可以使用的数学语言写成。
柯西说
我有严格的定义
简化版就是
类似这样{0.1、0.01、0.001,…}有无穷项,你随便选取一个数,我都能在序列中找到,某一项与0相减得到的差,使其绝对值小于你选的数,这就叫做无限趋近
有这样的一个实数序列随意挑个数,它之后的所有的数都比它小,那么这个序列的极限就是0,它在项数趋于无穷大时就是无穷小量。序列在无穷处就会无限趋近于0。
1无穷小量不是确定的量
2无穷小量不是一个实数
3无穷小量是以0为极限的变量
4无穷小量可以是序列
5无穷小量可以是函数
柯西的内心独白,我其实已经把无穷小量的概念抛弃了。
从这微积分就分家了
牛顿和莱布尼茨的微积分叫做无穷小微积分,有的书中写的是古典微积分
柯西之后微积分是极限微积分
或许我们永远都无法揭开“无穷小”的面纱,“人们的认知是无穷无尽的”,“无穷小”也会在不同的时代被赋予新的定义。
0.00…1(0.000中间无数个0最后加个1) 是什么
1)标准的实数体系
如果两个数的差值可以任意小,则这两个数相等也就是两个实数之间不存在任何数
在一个数轴上曾经有1、2、3…后来 1和2之间插进了分数1/10,2/10,…后来根号2这种无理数又插进去了,数之间是很稠密的,插不进去叫实数是完备的
0.00…1在数轴上找不到位置啊
2)超实数标准(非标准)
无穷小是一个数,无穷大也是一个数,0.00…1能当个无穷小吗,在超实数里面找到自己的位置;还是就换成了希腊字母,放在标准与非标准之外。