动态规划

一.什么是动态规划
动态规划（Dynamic Programming）是一种分阶段求解决策问题的数学思想。
一般包含三个重要的概念：最优子结构，边界，状态转移公式。
总结起来就是一句话：大事化小，小事化了。

二. 题目：
有一座高度是10级台阶的楼梯，从下往上走，每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法。

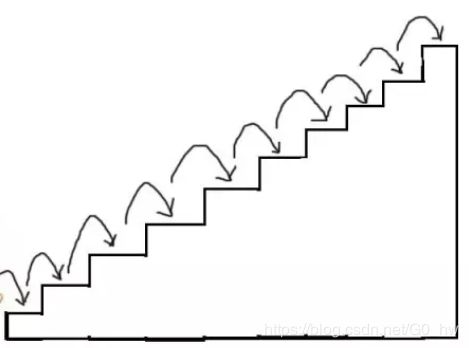
比如，每次走1级台阶，一共走10步，这是其中一种走法。我们可以简写成1,1,1,1,1,1,1,1,1,1。
再比如，每次走2级台阶，一共走5步，这是另一种走法。我们可以简写成 2,2,2,2,2。
当然，除此之外，还有很多很多种走法。

问题分析：
假设你只差最后一步就走到第10级台阶，这时会出现几种情况？
当然是下面的两种情况了：因为每一步只允许走1级或2级台阶，
(1)第一种情况从第9级台阶走1级到第10级；
(2)第二种情况从第8级台阶走2级到第10级；
那么，好了咱们先不管从0走到8级或9级台阶的过程，想要走到第10级，最后一步必然是从第8级或者第9级开始。
由此可以引申出一个新的问题：假设我们已知0到9级台阶的走法有X种，0到8级台阶的走法有Y种，那么0到10级台阶的走法有多少种？

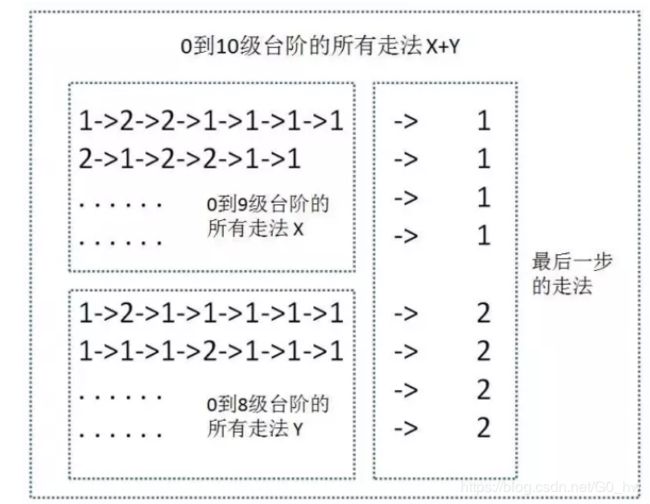
问题建模：
这样一来可以推导出一个结论：从0到10级台阶的走法数=从0到9级台阶的走法数 + 从0到8级台阶的走法数，即F(10) = F(9) + F(8),利用这个思路很容易推导出：F(9) = F(8) + F(7),F(8) = F(7) + F(6)…,当只有1级或者2级台阶的时候显然分别有1和2种走法，即F(1) = 1,F(2) = 2,由此，我们可以归纳出如下求解公式：
F(1) = 1;
F(2) = 2;
F(n) = F(n-1) + F(n-2); (n >= 3)
这里我们分析出F(10) = F(9) + F(8),因此F(9)和F(8)是F(10)的***最优子结构***；
当只有1级或者2级台阶时，我们可以直接得出结果，无需继续简化，因此可以称F(1)和F(2)是问题的***边界***，如果一个问题没有边界，将永远无法得到有限的结果；
F(n) = F(n-1) + F(n-2)是阶段与阶段之间的***状态转移方程***，这是动态规划的核心，决定了问题的每一个阶段和下一个阶段的关系；

问题求解：

    /**
     *  普通递归
     *  时间复杂度：O(2 ^ N)
     * @param n
     * @return
     */
    public static int getClimbingWays(int n){
        if (n < 1) {
            return 0;
        }

        if (n == 1) {
            return 1;
        }

        if (n == 2) {
            return 2;
        }

        return getClimbingWays(n-1) + getClimbingWays(n-2);
    }

时间复杂度分析：

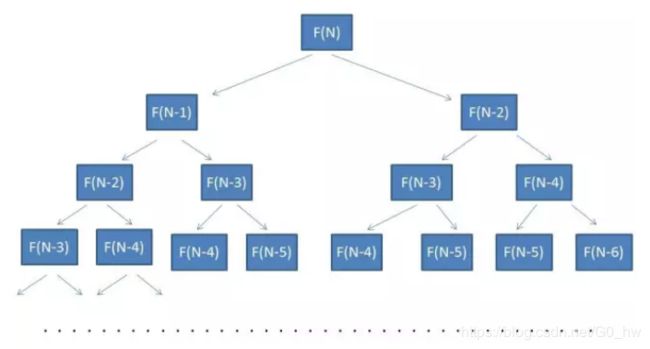
这种递归计算的过程就构成了一颗二叉树，树的节点个数就是我们的递归方法所需要计算的次数，不难看出这颗二叉树的高度为N-1,节点个数接近2的N次方，所以方法的时间复杂度可以近似的看作是O(2 ^ N).

递归的优化：
从上面的递归树状图可以看出，有些相同的参数被重复计算了，越往下走，重复的越多。

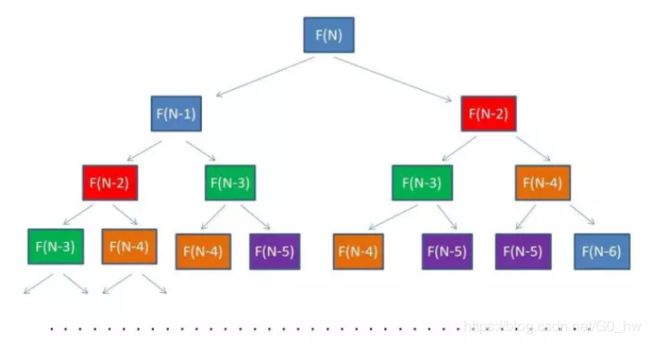
备忘录算法
那么如何避免这种重复计算的情况呢？
使用备忘录算法，用缓存暂存计算结果，先创建一个hash表，每次把不同参数的计算结果存入hash，但遇到重复参数时，直接从hash里面取值就行了。

/**
     * 备忘录算法
     * @param n
     * @param map 备忘录
     * @return
     */
    public static int getClimbingWays2(int n,Map<Integer,Integer> map){
        if (n < 1) {
            return 0;
        }

        if (n == 1) {
            return 1;
        }

        if (n == 2) {
            return 2;
        }

        if (map.containsKey(n)){
            return map.get(n);
        }

        int value = getClimbingWays2(n - 1,map) + getClimbingWays2(n - 2,map);
        map.put(n,value);
        return value;
    }

从F(1)到F(N)一共有N个不同的输入，在hash表里寸了N-2个结果，所以时间和空间复杂度都为O(N)。

    /**
     * 尾递归：重复利用栈帧.可以转成迭代算法，本质是将单次计算的结果缓存起来，传递给下次调用，相当于自动累积
     * Java编译器目前还不支持这种优化
     * 优点：
     ①计算结果参与到下一次的计算，从而减少很多重复计算量
     ②原本朴素的递归产生的栈的层次像二叉树一样，以指数级增长，但是现在栈的层次却像是数组，
     变成线性增长了，简单来说，原本栈是先扩展开，然后边收拢边计算结果，
     现在却变成在调用自身的同时通过参数来计算。
     * @param n
     * @param a
     * @param b
     * @return
     */
    public static int getClimbingWays(int n,int a,int b){
        if (n < 1) {
            return 0;
        }

        if (n == 1) {
            return 1;
        }

        if (n == 2) {
            return 2;
        }

        if (n == 3) {
            return a + b;
        }

        return getClimbingWays(n-1,b,a + b);
    }

动态规划：进一步压缩空间复杂度
我们一定要对F(N)做自顶向下的递归运算吗？可不可以自底向上用迭代的方式推导出结果？
F(N)自底向上求解过程图解。

F(1)和F(2)是已经明确的结果。

第一次迭代，F(3)只依赖于F(1)和F(2).

第二次迭代，F(4)只依赖于F(2)和F(3).
。。。
由此可见：每一次迭代过程中，只要保留之前的两个状态，就可以推导出新的状态，而不需要像备忘录算法那样保留所有的子状态。这才是真正的动态规划实现。

    /**
     * 动态规划:利用简洁的自底向上的思维实现，实现时间和空间上的最优化
     * 时间复杂度：O(N)
     * 空间复杂度：O(1)
     * @param n
     * @return
     */
    public static int getClimbingWays3(int n){
        if (n < 1) {
            return 0;
        }

        if (n == 1) {
            return 1;
        }

        if (n == 2) {
            return 2;
        }

        int a = 1;
        int b = 2;
        int temp = 0;
        for (int i=3;i<=n;++i){
            temp = a + b;
            a = b;
            b = temp;
        }
        return temp;
    }