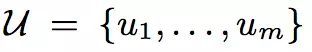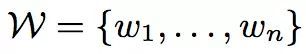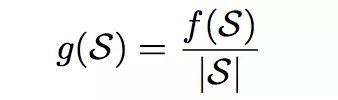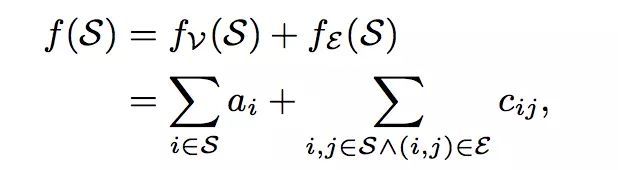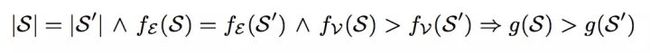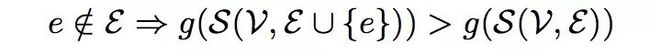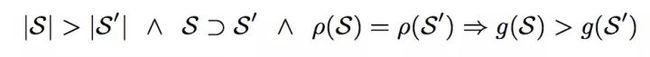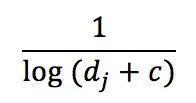《Graph Learning专栏》 ： 高密子图挖掘

本周我们介绍另一图上的“聚类”算法—高密子图挖掘(Dense Subgraph Mining)，这类算法与社群检测不同的是处理的数据对象是异构图(节点的类型不是单一的，同类型节点之间一般没有边)，社群检测需要对整张图的节点进行社区划分，而高密子图只关心最紧密的那个社区；相同的是二者都是同一种思考模式：定义一个衡量密集度的指标，启发式地不断优化这个值。

lockstep行为模式

在实际应用场景中，高密子图一般用作团伙欺诈检测。因为这类算法找到的最致密的社区一般预示着一种同步的、大量的关联行为模式，这种行为模式称之为lockstep，而且往往比较契合现实场景中欺诈团伙的本质特点。比如水军账号团伙在进行恶意评分、虚假点赞时，都会产生这样的行为模式。

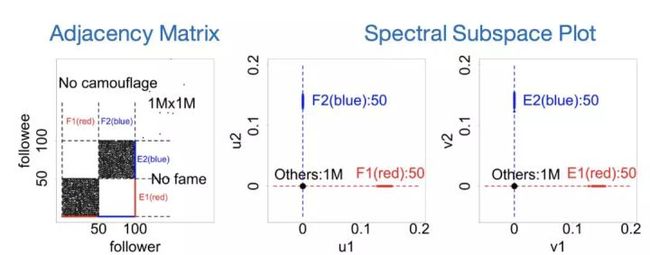
lockstep模式从图上面看，是要找到联系紧密的二部图结构，这种结构对应着邻接矩阵上的某个Dense Block。在《EigenSpokes: Surprising Patterns and Scalable Community Chipping in Large Graphs 》一文中，作者探讨了这种模式在谱空间上的可视化效应：

上图就是对邻接矩阵进行SVD分解，然后将u向量与v向量的前两列分别可视化出来的结果。作者得到的一个基本结论就是这类模式会在谱空间上有明显的聚类现象，谱空间上的每一簇都对应着邻接矩阵上的某个Dense Block。利用这个现象，可以十分方便地观察到图里面的高密子图结构。

 

但是如何让这个发现过程自动化，以及避免SVD分解的高时间复杂度呢？下面要讲解的FRAUDAR算法，可以很好地实现这个目标。

 

FRAUDAR算法

FRAUDAR 算法自动化地挖掘出二部图里的高密子图，同时对欺诈者的伪装行为(Camouflage )具有非常好的对抗性，线性时间复杂度也使得该算法在工业级的业务数据上具有很好的适用性，并获得了 KDD2016的最佳论文奖。

 

下面来看看本文怎么寻找高密子图：

问题定义

考虑在用户对商品进行评分的场景中，m个用户构成

n件商品构成

用户与商品之间构成二部图

我们需要找到可疑的欺诈用户。更多的符号约定如下：

度量指标

为了度量我们找到的社区的可疑度，作者定义了一个十分简单的度量指标：

 

表示社区S内的 第i个节点的可疑度，

表示社区内i节点与j节点构成边的可疑度。

 

一般

可以通过先验的，其他方面的信息来给出节点的可疑度，后文中将这个值都设为0。

可用边的权重代替，最特殊的情况是都取值为1，这样整个可疑度的度量指标就退化成了社区内边的密度了。

 

为了说明这个度量指标的合理性，作者证明了该度量指标具有以下4个性质：

1.node suspiciousness：节点的可疑度越高，社区的可疑度越高。

2.edge suspiciousness：边的可疑度越高，社区的可疑度越高。

3.size：边密度一样，越大的社区可疑度越高。

4.concentration：节点和边的可疑度之和一样，越小的社区可疑度越高。

算法

同很多启发式算法一样，有了这个度量指标之后，就可以贪心地去优化这个值。具体来说，就是从整张图开始，不断重复地删除某个节点，使剩下的图的可疑度指标最大。这里一个核心加速的地方在于：删除某个节点i，仅仅只会影响到与i节点相连的节点结构发生变化。由于本文使用的度量指标最终为社区边的密度，所以每次只需要考虑删除度最小的节点，然后更新与之相连节点的度即可，这个不断更新最小度的过程可以通过优先树这种数据结构快速实现。

 

下面我们给出算法步骤：

可以看到，算法不断删除节点使得剩下的节点构成的社区可疑度最大，然后记录整个删除过程中社区可疑度最大的那一轮，那么该轮的剩余节点构成的子图就是最可疑的。

对抗伪装

前面我们讲了怎样使用启发式地算法快速寻找图中的高密子图，但是这里面存在两方面的问题：

1. 真实用户与流行商品之间会形成一个天然联系紧密的 Dense Block，算法怎么区分这类社区与欺诈行为形成的社区？
2. 欺诈者可以通过与流行商品之间的互动来伪装自己，比如随机评论一些其他商品或者流行商品来伪装自己的数据表现形式，如下图：

对于上述两个问题，如何解决呢？

 

这里面很核心的一点是，不管怎么伪装，对于那些买评分的商品，欺诈用户的评分权重占比更高，而其他商品真实用户的评分权重占比更高。考虑清楚了这一点之后，我们可以对边ij的可疑度Cij根据列节点的度(weight sum of column)进行降权操作。比如某件商品j的度越高，那么就要将cij处理的越低，这是因为度很高的商品并不是一定可疑的，比如流行商品，同时以这种方式对边的可疑度进行重新分配，完全不会降低欺诈社区的可疑度。大家可以对照上面图中两种伪装方式，考虑伪装前与伪装后社区可疑度的变化就明白这个道理了。

 

具体地，本文使用的降权函数为

c为一个常数，实验中设置为5。该算法在后文的一系列工业界数据集实验上面都取得了最好成绩。

Dense Subtensor

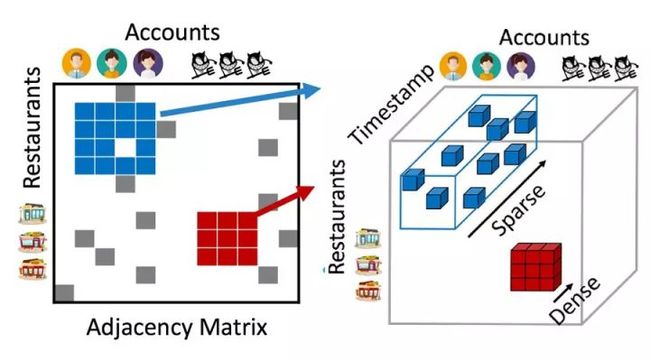
上面的FRAUDAR算法只是在二部图中挖掘高密子图，当数据具有更高维度时，比如一个转发帖子的场景中，每条数据都对应着账户、IP、帖子ID、时间这4维信息，数据因此而构成了一个 4 阶张量Tensor。我们的任务变成了在这个高维 Tensor 中寻找 Dense Subtensor。虽然数据的维度变高了，但是解决问题的思路同 FRAUDAR 算法还是一致的，比如 M-Zoom、D-Cube 这两类 Dense Subtensor Mining 算法，都是先定义一个度量指标，然后启发式迭代优化，有兴趣的可以自己去看看相关论文。

 

一般来说，在高维数据中，如果还能找到密集区域，那么会大大增加区域的可疑度。因为这需要更多的维度信息进行交叉印证，正常用户群体最多在 2 维空间上聚集，我们可以看下面两个图的对比：

欢迎关注我们的微信公众号：极验（geetest_jy）添加技术助理：geetest1024入群交流！

参考文献：

EigenSpokes：

http://people.cs.vt.edu/badityap/papers/eigenspokes-pakdd10.pdf

FRAUDAR：

https://www.cs.cmu.edu/~neilshah/research/papers/FRAUDAR.KDD.16.pdf

M-Zoom：

https://www.cs.cmu.edu/~kijungs/papers/mzoomPKDD2016.pdf

D-Cube：

http://www.cs.cmu.edu/~kijungs/papers/dcubeWSDM2017.pdf