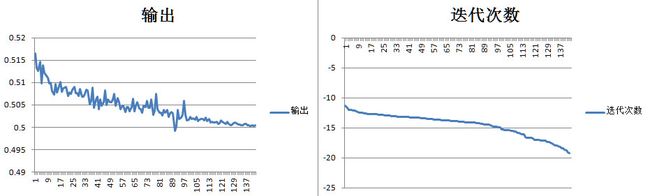
由神经网络的迭代次数计算输出值并评价网络性能

在《用共振频率去理解神经网络-将乙烯模型运行300次的数据》文中将乙烯模型运行了300次，得到了300组输出与迭代次数的数据。这次计算只用了其中的150组数据，其中的6组明显不合理被剔除了，由余下的144组数据可以非常直观的发现迭代次数与输出值高度相关。

  
 

 

*	输出	迭代次数	迭代次数
2	0.516509	86713	-11.3704
3	0.513156	124593	-11.7328
4	0.512544	164576	-12.0111
5	0.514564	169478	-12.0405
6	0.509862	169959	-12.0433
7	0.513865	184908	-12.1276
8	0.512103	188896	-12.149
9	0.511447	204082	-12.2263
10	0.511093	231931	-12.3542
11	0.509828	253718	-12.444

 

 

81	0.503994	1349560	-14.1153
82	0.503236	1381406	-14.1386
83	0.50333	1386255	-14.1421
84	0.502709	1395038	-14.1484
85	0.503829	1447198	-14.1851
86	0.503246	1486612	-14.212
87	0.503802	1596727	-14.2835
88	0.502321	1749888	-14.3751
89	0.503119	1776919	-14.3904
90	0.503425	1848841	-14.4301

 

 

 

 

131	0.501003	34099800	-17.3448
132	0.500885	37053436	-17.4279
133	0.500538	46023712	-17.6447
134	0.500605	58152875	-17.8786
135	0.500485	59579395	-17.9028
136	0.500408	60055128	-17.9108
137	0.500737	70086877	-18.0652
138	0.500707	74569401	-18.1272
139	0.500511	93937143	-18.3581
140	0.500373	94650373	-18.3657

 

 

 

通过这个表格很容易的发现随着迭代次数的增加输出越来越小逼近0.5，由于输出的变化范围太大，做了数学变换-ln（x），将输出和变换后的迭代次数画成图

 

 

 

 

可以相当直观的看出迭代次数和输出肯定是有关系的，但不知道是什么关系，这里先假设是简单的线性关系，用一次函数去拟合这两组数据

输出的函数y2=k2*x+b2

迭代次数的函数y1=k1*x+b1

先对输出图像做平滑，然后抽出两组值比如

0.5086	14
0.5007	136

可以算出

k2=	-6.47541E-05
b2=	0.509506557

 

然后迭代次数也取两组值比如

-12.74	18
-17.9	134

算出

k1=	-0.044482759
b1=	-11.93931034

将x代入可以得到

Y(输出)=0.001455712*（-ln（X)）+0.526886758---a

X就是迭代次数

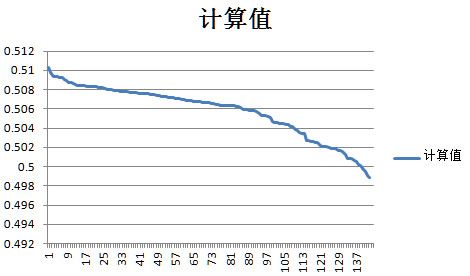
得到图像

 

 

 

可以通过公式a简单由迭代次数去计算输出值，得到的平均误差是0.0023也就是0.23%，对于有效位数是在千分位和万分位的数字来说这个误差还是太大的，应该是有其他的规律，但对固定结构固定输入的神经网络的输出值是可以被计算的这个总是肯定的。输入权重可以影响迭代次数，但不会改变网络的特征输出。

虽然在网络运行前不太可能知道会迭代多少次，但运行几次得到几组数据之后，可以用这种近似的办法得到这个网络特征输出，并用特征输出和期望值的差距去判断网络的总体性能。

/***************************************************************************************************************/

后经大量实验证实神经网络在收敛标准，权重初始化方式，学习率不变的情况下神经网络的输出和迭代次数的关系更接近

输出=系数a*ln（迭代次数）

Y=a.ln（n）

在2018年10月21日《用神经网络模拟分子：数据重复性检测》中构造了同系列的34组网络，实验表明迭代次数随着网络结构的变化曾高度规则变化，网络越复杂理论收敛迭代次数n越大，特征明显高度可重复，Y值也呈高度规则变化。在2018年10月21日《用神经网络模拟分子：数据精确性检测》中有更为详细的数据。

在2018年11月17日《神经网络结构与输出值之间的关系》有输出值变化规律的详细数据。

 

 

 

实验数据

*	输出	迭代次数	迭代次数	计算值	误差
2	0.516509	86713	-11.3704	0.510335	-0.01195
3	0.513156	124593	-11.7328	0.509807	-0.00653
4	0.512544	164576	-12.0111	0.509402	-0.00613
5	0.514564	169478	-12.0405	0.509359	-0.01012
6	0.509862	169959	-12.0433	0.509355	-0.00099
7	0.513865	184908	-12.1276	0.509232	-0.00901
8	0.512103	188896	-12.149	0.509201	-0.00567
9	0.511447	204082	-12.2263	0.509089	-0.00461
10	0.511093	231931	-12.3542	0.508903	-0.00429
11	0.509828	253718	-12.444	0.508772	-0.00207
12	0.509942	263930	-12.4834	0.508714	-0.00241
13	0.508077	275618	-12.5268	0.508651	0.00113
14	0.507283	293796	-12.5906	0.508558	0.002513
15	0.509628	313571	-12.6558	0.508464	-0.00229
16	0.507789	320830	-12.6787	0.50843	0.001262
17	0.508679	322715	-12.6845	0.508422	-0.00051
18	0.510065	330262	-12.7076	0.508388	-0.00329
19	0.507998	342228	-12.7432	0.508336	0.000666
20	0.508769	346631	-12.756	0.508318	-0.00089
21	0.508902	347396	-12.7582	0.508314	-0.00116
22	0.508954	348106	-12.7603	0.508311	-0.00126
23	0.507023	357612	-12.7872	0.508272	0.002464
24	0.507826	369138	-12.8189	0.508226	0.000788
25	0.507427	373511	-12.8307	0.508209	0.00154
26	0.508347	385912	-12.8634	0.508161	-0.00036
27	0.50897	414579	-12.935	0.508057	-0.00179
28	0.507568	435026	-12.9832	0.507987	0.000825
29	0.507557	435726	-12.9848	0.507985	0.000842
30	0.506943	445736	-13.0075	0.507952	0.001989
31	0.508557	460928	-13.041	0.507903	-0.00129
32	0.50686	465972	-13.0519	0.507887	0.002026
33	0.506789	467585	-13.0553	0.507882	0.002156
34	0.507385	496763	-13.1159	0.507794	0.000806
35	0.508386	510314	-13.1428	0.507755	-0.00124
36	0.508223	510541	-13.1432	0.507754	-0.00092
37	0.505149	512141	-13.1464	0.507749	0.005148
38	0.505831	516517	-13.1549	0.507737	0.003767
39	0.508849	520660	-13.1629	0.507725	-0.00221
40	0.504402	532222	-13.1848	0.507693	0.006525
41	0.506183	551801	-13.2209	0.507641	0.002881
42	0.506764	553739	-13.2244	0.507636	0.00172
43	0.504039	572627	-13.258	0.507587	0.007038
44	0.506264	575598	-13.2632	0.507579	0.002598
45	0.504858	585025	-13.2794	0.507556	0.005343
46	0.505587	586087	-13.2812	0.507553	0.003889
47	0.50819	596912	-13.2995	0.507526	-0.0013
48	0.50504	615982	-13.331	0.507481	0.004833
49	0.506155	618640	-13.3353	0.507474	0.002607
50	0.505588	645834	-13.3783	0.507412	0.003607
51	0.505614	671661	-13.4175	0.507355	0.003443
52	0.506141	693969	-13.4502	0.507307	0.002304
53	0.507431	699873	-13.4587	0.507295	-0.00027
54	0.504775	717198	-13.4831	0.507259	0.004922
55	0.506531	750614	-13.5286	0.507193	0.001306
56	0.505581	755332	-13.5349	0.507184	0.003171
57	0.504047	785305	-13.5738	0.507127	0.006111
58	0.504673	802453	-13.5954	0.507096	0.004801
59	0.504772	838870	-13.6398	0.507031	0.004476
60	0.503381	840281	-13.6415	0.507029	0.007246
61	0.504552	868670	-13.6747	0.50698	0.004814
62	0.504552	887241	-13.6959	0.50695	0.004752
63	0.503548	934152	-13.7474	0.506875	0.006607
64	0.504572	944298	-13.7582	0.506859	0.004532
65	0.506335	970624	-13.7857	0.506819	0.000956
66	0.5036	989617	-13.8051	0.506791	0.006335
67	0.504758	1001063	-13.8166	0.506774	0.003994
68	0.505566	1004941	-13.8204	0.506768	0.002377
69	0.504216	1049234	-13.8636	0.506705	0.004937
70	0.50407	1069259	-13.8825	0.506678	0.005175
71	0.503195	1092914	-13.9044	0.506646	0.006857
72	0.504737	1098825	-13.9098	0.506638	0.003767
73	0.504522	1100358	-13.9111	0.506636	0.00419
74	0.505833	1194748	-13.9934	0.506516	0.001351
75	0.50431	1200766	-13.9985	0.506509	0.004361
76	0.504304	1242820	-14.0329	0.506459	0.004272
77	0.506197	1264917	-14.0505	0.506433	0.000467
78	0.50279	1305698	-14.0822	0.506387	0.007154
79	0.503678	1309950	-14.0855	0.506382	0.00537
80	0.507389	1335669	-14.1049	0.506354	-0.00204
81	0.503994	1349560	-14.1153	0.506339	0.004653
82	0.503236	1381406	-14.1386	0.506305	0.006098
83	0.50333	1386255	-14.1421	0.5063	0.005901
84	0.502709	1395038	-14.1484	0.506291	0.007125
85	0.503829	1447198	-14.1851	0.506237	0.00478
86	0.503246	1486612	-14.212	0.506198	0.005866
87	0.503802	1596727	-14.2835	0.506094	0.00455
88	0.502321	1749888	-14.3751	0.505961	0.007247
89	0.503119	1776919	-14.3904	0.505938	0.005605
90	0.503425	1848841	-14.4301	0.505881	0.004879
91	0.50304	1895990	-14.4553	0.505844	0.005573
92	0.499132	1901928	-14.4584	0.50584	0.013439
93	0.500181	1993833	-14.5056	0.505771	0.011175
94	0.503893	2053206	-14.5349	0.505728	0.003641
95	0.501926	2314784	-14.6548	0.505554	0.007226
96	0.502172	2671842	-14.7983	0.505345	0.006318
97	0.502766	2679391	-14.8011	0.505341	0.00512
98	0.505906	2745179	-14.8254	0.505305	-0.00119
99	0.502758	2888629	-14.8763	0.505231	0.004919
100	0.501576	3096264	-14.9457	0.50513	0.007086
101	0.501632	4090919	-15.2243	0.504725	0.006164
102	0.502274	4503546	-15.3204	0.504585	0.004599
103	0.501819	4662151	-15.355	0.504534	0.00541
104	0.502067	4884791	-15.4016	0.504466	0.00478
105	0.501729	4907008	-15.4062	0.50446	0.005443
106	0.502375	4931587	-15.4112	0.504453	0.004136
107	0.501388	5158308	-15.4561	0.504387	0.005982
108	0.501764	5170149	-15.4584	0.504384	0.005221
109	0.501843	6139307	-15.6302	0.504134	0.004564
110	0.501899	6192504	-15.6389	0.504121	0.004428
111	0.501531	7285906	-15.8015	0.503884	0.004692
112	0.502156	7856737	-15.8769	0.503775	0.003223
113	0.50146	9053680	-16.0187	0.503568	0.004204
114	0.501843	9606597	-16.078	0.503482	0.003266
115	0.50107	9920757	-16.1101	0.503435	0.004719
116	0.501184	16322171	-16.608	0.50271	0.003044
117	0.501048	16810859	-16.6375	0.502667	0.003231
118	0.50107	17221260	-16.6617	0.502632	0.003118
119	0.501193	17654126	-16.6865	0.502596	0.002799
120	0.500803	18346351	-16.7249	0.50254	0.003468
121	0.500974	18675513	-16.7427	0.502514	0.003074
122	0.501474	23812301	-16.9857	0.50216	0.00137
123	0.501195	24330009	-17.0072	0.502129	0.001864
124	0.500943	24577379	-17.0173	0.502114	0.002337
125	0.5007	25078250	-17.0375	0.502085	0.002766
126	0.501205	26386757	-17.0884	0.502011	0.001609
127	0.50077	28370298	-17.1609	0.501905	0.002268
128	0.500445	28796741	-17.1758	0.501884	0.002875
129	0.500585	29173786	-17.1888	0.501865	0.002557
130	0.500871	33265639	-17.32	0.501674	0.001603
131	0.501003	34099800	-17.3448	0.501638	0.001267
132	0.500885	37053436	-17.4279	0.501517	0.001262
133	0.500538	46023712	-17.6447	0.501201	0.001325
134	0.500605	58152875	-17.8786	0.500861	0.000511
135	0.500485	59579395	-17.9028	0.500825	0.000679
136	0.500408	60055128	-17.9108	0.500814	0.000811
137	0.500737	70086877	-18.0652	0.500589	-0.0003
138	0.500707	74569401	-18.1272	0.500499	-0.00042
139	0.500511	93937143	-18.3581	0.500163	-0.0007
140	0.500373	94650373	-18.3657	0.500152	-0.00044
141	0.500299	131563386	-18.695	0.499672	-0.00125
142	0.500419	148811826	-18.8182	0.499493	-0.00185
143	0.50031	198305891	-19.1053	0.499075	-0.00247
144	0.500405	221802724	-19.2173	0.498912	-0.00298
*
平均值	0.504635	13009477.13	-14.4947	0.505787	0.002299