奇异递归模板模式(CRTP)应用--表达式模板(expression template) 2
1 表达式模板(expression template)概述
首先分几个部分介绍下expression template。
1.1 表达式模板(expression template)是什么?
引用wiki 介绍的 Expression templates :
Expression templates are a C++ template metaprogramming technique that builds structures representing a computation at compile time, which structures are evaluated only as needed to produce efficient code for the entire computation. Expression templates thus allow programmers to bypass the normal order of evaluation of the C++ language and achieve optimizations such as loop fusion.
Expression templates were invented independently by Todd Veldhuizen and David Vandevoorde; it was Veldhuizen who gave them their name.They are a popular technique for the implementation of linear algebra software.
结合上面的介绍,简单总结下expression template,表达式模板(expression-template)是一种C++模板元编程技术,它在编译时刻构建好一些能够表达某一计算的结构,对于整个计算这些结构仅在需要(惰性计算、延迟计算)的时候才产生相关有效的代码运算。因此,表达式模板允许程序员绕过正常(这里不知如何翻译,其实可以理解写程序的一般做法吧)的C++语言计算顺序,从而达到优化计算的目的,如循环合并。Expression template是Todd Veldhuizen & David Vandevoorde 发明的,详情见其技术报告:Veldhuizen, Todd (1995). “Expression Templates”. C++ Report.。expression template技术在线性代数相关软件中应用十分广泛,比如Eigen、 Boost uBLAS等等。
1.2 为什么引入 expression template
先通过一个例子来说明,假设在机器学习中我们现在需要构造一个类,这个类有size_ 维feature,每个feature的值是个double类型的实数,这个类不同对象间的同一维度的feature可以进行简单的算术运算(比如+、- maximum…),比较简单的思想是进行运算符重载,具体见代码:
// a naive solution( bad! )
// operator overloading
#include 因为我们这个类涉及资源申请,因此需要实现普通构造函数、拷贝构造、赋值构造、析构(其实C++11里实现移动构造、移动赋值更佳,后面会code说明)。运行结果如下:

对于实现d=a+b+c这样的多个连加的表达式,我们可以看到它进行多次对象的构造(对象a、b、c进行三次普通对象构造(必需),然后按照+的顺序进行运算,按照计算顺序,表达式其实是这样的d=((a+b)+c)),首选a+b相加会构造一个临时对象,a、b相加的结果(这里假设a+b=tmp1)返会又要进行拷贝构造,然后表达式实际变成d=tmp1+c, tmp1和c相加又会构造一个临时对象(这里假设为tmp2,即有tmp1+c=tmp2),然后tmp2拷贝构造生成最终的结果d,细数下简单的连加进行了很多对象的构造析构(其实就是很多次内存的申请和释放,这个效率不要太低!!!)。仿佛听到有童鞋高呼我们可以用C++11的移动语义,来减少临时对象(内存的频繁申请、释放)频繁内存操作,好先上代码:
// move constructor
MyType(MyType&& rhs) :size_(rhs.size()) {
features_ = rhs.features_;
rhs.size_ = 0;
rhs.features_ = nullptr;
cout << "\tMyType move constructor size = " << size_ << "\n";
}
// move assignment
MyType& operator=(MyType&& rhs) {
if (this != &rhs) {
size_ = rhs.size_;
rhs.size_ = 0;
features_ = rhs.features_;
rhs.features_ = nullptr;
cout << "\tMyType move assignment constructor size = " << size_ << "\n";
}
*this;
}即是利用C++11的移动语义(move constructor 、assignment constructor )来减少内存的重复申请与释放,然而对于d = a + b + c 这样连加的case至少需要有一次临时内存的申请与释放和两次加操作的循环(如下图,标号1的内存即为a+b=tmp1构造过程,对象tmp1存放临时结果,当tmp1与c相加即有tmp1+c=tmp2,再生成tmp2后tmp1便释放内存,tmp2用移动构造出连加结果d),因此,下面不得不引入一个大杀器 expression template。

注意 上面几张图的结果是在vs2015上编译的结果,可见没进行NRVO(named return value optimization),进行了RVO即Return Value Optimization,是一种编译器优化技术,可以把通过函数返回创建的临时对象给”去掉”,然后可以达到少调用拷贝构造的操作。号外,这篇有介绍 RVO和std::move的原理 的文章,可以看下。所以采用不同的编译器以及优化等级可能结果和上图不同, g++ 默认是开启了 NRVO,可以加上这个编译参数-fno-elide-constructors 去掉NRVO,详细的测试可以参见,下面给出的github地址。
1.3 expression template 想解决的问题
引用wiki More C++ Idioms/Expression-template 所说的Express Template的意图:
Intent
- To create a domain-specific embedded language (DSEL) in C++.
- To support lazy evaluation of C++ expressions (e.g., mathematical expressions), which can be executed much later in the program from the point of their definition.
- To pass an expression – not the result of the expression – as a parameter to a function.
总结来说其实Expression Template想要解决的问题是:
1. 在C++中创建一个嵌入式领域专用语言(DSEL)(大概意思就是在一个编程语言里嵌入一个领域特定语言。参考 这个 Domain Specific Languages in C++ )。
2. 支持表达式的懒惰计算(延迟计算),相对其定义它可以推迟表达式的计算。
3. 传递一个表达式,不是表达式的结果而是把表达式自身作为一个参数传给一个函数。
1.4 expression template的方法
结合1.2中的naive operator overloading下面举例说明表达式模板的神奇功效,先show代码(对CRTP技术不了解的请先看我之前写的奇异递归模板模式( Curiously Recurring Template Pattern,CRTP)1):
// expression template
// Copyright (C) 2017 http://ustcdane.github.io/
#include > {
BinaryOp(const TLhs& lhs, const TRhs& rhs):lhs_(lhs.cast()), rhs_(rhs.cast()) {}
// work function, computing this expression at position i, import for lazy computing
double value(int i) const {
return Func::Op(lhs_.value(i), rhs_.value(i));
}
int size() const { return std::max(lhs_.size(), rhs_.size()); }
private:
const TLhs& lhs_;
const TRhs& rhs_;
};
// template binary operation, works for any expressions
template<typename Func, typename TLhs, typename TRhs>
inline BinaryOp
expToBinaryOp(const Expression& lhs, const Expression& rhs) {
return BinaryOp(lhs.cast(), rhs.cast());
}
// binary operators +
struct Add {
// any function defined inside its class definition is inline
static double Op(double a, double b) {
return a + b;
}
};
// define Minimum
struct Minimum {
static double Op(double a, double b) {
return a < b ? a : b;
}
};
template<typename TLhs, typename TRhs>
inline BinaryOp
operator+(const Expression& lhs, const Expression& rhs) {
return expToBinaryOp(lhs, rhs);
}
template<typename TLhs, typename TRhs>
inline BinaryOp
min(const Expression& lhs, const Expression& rhs) {
return expToBinaryOp(lhs, rhs);
}
// allocation just by user
// no constructor and destructor to allocate and de-allocate memory
class MyExpType : public Expression {
public:
MyExpType():size_(0) {}
MyExpType(double *features, int size)
: size_(size), features_(features) {
printf("MyExpType constructor size = %d. No memory allocate.\n", size_);
}
// delete copy constructor,
MyExpType(const MyExpType& src_) = delete;
template<typename ExpType>
MyExpType(const Expression& src_) = delete;
// here is where computing happens,lazy support
template<typename ExpType>
MyExpType& operator=(const Expression& src) {
const ExpType &srcReal = src.cast();
assert(size_ >= srcReal.size()); //
for (int i = 0; i < srcReal.size(); ++i) {
features_[i] = srcReal.value(i); // binary expression value work function
}
printf("MyExpType assignment constructor size = %d\n", size_);
return *this;
}
// computing function
double value(int i) const { return features_[i]; }
int size() const { return size_; }
private:
int size_;
double* features_;
};
void print(const MyExpType& m) {
printf("( ");
for (int i = 0; i < m.size() - 1; ++i) {
printf("%g, ", m.value(i));
}
if (m.size())
printf("%g )\n", m.value(m.size()-1));
else
printf(" )\n");
}
int main() {
const int N = 3;
double sa[N] = { 1.1,1.1, 1.1 };
double sb[N] = { 2.01, 2.01, 2.01 };
double sc[N] = { 3.01, 3.01, 3.01 };
double sd[N] = { 0 };
MyExpType A(sa, N), B(sb, N), C(sc, N), D(sd, N);
printf("\n");
printf(" A = "); print(A);
printf(" B = "); print(B);
printf(" C = "); print(C);
printf("\n\tD = A + B + C\n");
D = A + B + C;
for (int i = 0; i < A.size(); ++i) {
printf("%d:\t%g + %g + %g = %g\n",
i, B.value(i), C.value(i), B.value(i), D.value(i));
}
printf("\n\tD = A + min(B, C)\n");
// D = A + expToBinaryOp(B, C);
D = A + min(B, C);
for (int i = 0; i < A.size(); ++i) {
printf("%d:\t%g + min(%g, %g) = %g\n",
i, A.value(i), B.value(i), C.value(i), D.value(i));
}
return 0;
} 程序运行结果如下图:
如上图所示,看到expression template的神奇了吧,我们的类这下没有内存申请、释放(用户给一个有效地址内存及size即可),三连加只有一次赋值构造,无内存申请、释放,而且只有一次循环。正像上一小节所说的,Expression template所要解决是延迟计算问题(lazy evaluation )。它可以在C++中让operator+返回自定义类型来实现这一功能。当表达式比较长时可以有效的构建出表达式树 如分析树(parse tree)这样的形式 。对应到本程序的表示式 D=A+B+C ,其对应的表达(类型)树如下图所示,表达式的计算只在赋值(operator=)给一个实际对象时才进行。表达式模板通过在编译期的表达式树来实现延迟计算。
表达式右侧被解析为类型expToBinaryOp
for (int i = 0; i < D.size(); ++i) {
D.features_[i] = A.value(i) + B.value(i) + C.value(i);
} 2. 表达式模板demo
结合表达式模板的相关分析,实现了一个支持一元及二元自定义类型的表达式模板操作库(当然是用了CRTP技术),来段测试代码先:
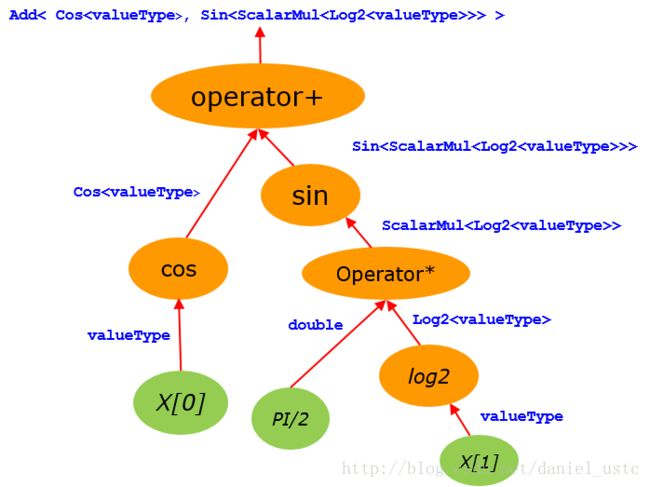
#include 分析:如代码中 algorithm3 y=cos(x[0]) +sin(PI/2*log2(x[1])),其对应的表达式类型树如下图所示:
具体为什么是这样的可以参考代码,其中ScalarMul是表达式类型和标量类型相乘的表达式类型。本文所有代码请到我的github。
3. Expression Template总结
expression template能让代码高效很多,即使现在最新的cpp11移动语义也不能达到我们所说的表达式模板连加的效率,尤其在代数计算领域,表达式模板更是实现相关工具的典范,有机会的话再写篇关于自动求导(automatic differentiation,AD)的文章吧(好像介绍CRTP技术的时候就说要写了…),也是利用了表达式模板的技术。
参考:
- wiki Expression_templates
- More C++ Idioms/Expression-template
- Modern C++ design
- mshadow Expression Template