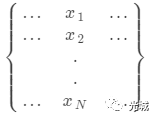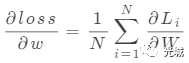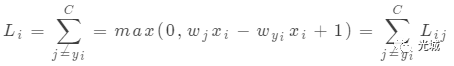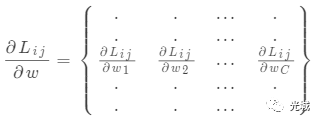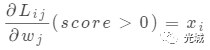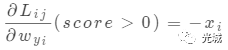cs231n之KNN、SVM
cs231n之KNN、SVM
0.说在前面1.KNN2.SVM3.作者的话
0.说在前面
最近在学习cs231n，觉得有点困难，今天抽了一晚上时间来写这篇文章，作为总结。下面一起来看任务一的题目，由于篇幅长，故分成两部分，下节重点softmax!
1.KNN
np.flatnonzero
该函数输入一个矩阵，返回扁平化后矩阵中非零元素的位置(index)！！！
一个特殊用法：
idxs = np.flatnonzero(y_train == y)
上面这行代码是knn中的可视化图像数据的一行代码，表示从y_train中找到label为y的index，具体的例子实战如下：
In:
import numpy as np
x = np.arange(-3,5)
Out:
array([-3, -2, -1, 0, 1, 2, 3, 4])
In:
np.flatnonzero(x)
Out:
array([0, 1, 2, 4, 5, 6, 7], dtype=int64)
In:
np.flatnonzero(x==-3)
Out:
array([0], dtype=int64)
np.random.choice
原型：
numpy.random.choice(a, size=None, replace=True, p=None)
从给定的一维数组中生成一个随机样本；
| 参数 | 参数意义 |
|---|---|
| a | 为一维数组或者int数据； |
| size | 为生成的数组维度； |
| replace | 是否原地替换； |
| p | 为样本出现的概率； |
样例：
np.random.choice(5,3) # 等价于np.random.randint(0,5,3)
p参数：
np.random.choice(5,3,p=[0,0,0.1,0.6,0.3])
注意p里面数量与a的数量一致，表示每个数随机选择的概率！
replace参数：
In:
a = ['bird','meh','sad','d','123']
np.random.choice(a,5) # replace默认为True
np.random.choice(a,5,replace=False)
Out:
array(['d', 'd', 'meh', '123', 'sad'], dtype='<U4')
array(['d', 'bird', 'meh', '123', 'sad'], dtype='<U4')
我们看到当replace为True的时候，也就是默认值，此时输出会重复，而设置为False，则输出不重复！！！
reshape中-1
In:
x = np.arange(-3,5)
x
Out:
array([-3, -2, -1, 0, 1, 2, 3, 4])
假设我们不知道这个数组多少行，我们想reshape成(8,1)，那么如何通过-1来实现？
-1可以自动计算出数组的列数或行数
In:
x.reshape(-1,1)
Out:
array([[-3],
[-2],
[-1],
[ 0],
[ 1],
[ 2],
[ 3],
[ 4]])
In
x.reshape(1,-1)
out:
array([[-3, -2, -1, 0, 1, 2, 3, 4]])
两层循环
首先看一下测试集与训练集的维度：
(5000, 3072) (500, 3072)
这里通过两层循环比较训练集和测试集的每一张图片的间距，最终得到(500,5000)的矩阵！
距离计算方法采用欧式距离计算！
# 传进来x_test shape(500,3072)
# self.X_train shape(5000,3072)
def compute_distances_two_loops(self, X):
# 500
num_test = X.shape[0]
# 5000
num_train = self.X_train.shape[0]
# 生成一个shape(500,5000)的全为0矩阵
dists = np.zeros((num_test, num_train))
# 两重for循环
for i in range(num_test):
for j in range(num_train):
# 利用欧式距离计算
dists[i，j]=np.sqrt(np.sum(np.square(X[i，:]-self.X_train[j，:])))
return dists
修改predict_labels
这里提示用argsort，先来学习一下这个argsort。
示例：
x = np.array([5,3,0,-1,9])
np.argsort(x)
输出：
array([3, 2, 1, 0, 4], dtype=int64)
上述可以得出，通过argsort可以返回数组当中的从小到大的索引数组！
# y_train shape(5000,)
def predict_labels(self, dists, k=1):
num_test = dists.shape[0]
y_pred = np.zeros(num_test)
# 上面两层循环的得出dists shape(500,5000)
# 下面通过循环来得出测试图片500张与训练图片5000张距离最近的前k个
for i in range(num_test):
closest_y = []
# 目的是得出测试图片500张与训练图片5000张距离最近的前k个
closest_y = self.y_train[np.argsort(dists[i，：])[:k]]
# 投票得出预测值
y_pred[i] = np.argmax(np.bincount(closest_y))
return y_pred
在对k个图片投票时候，得票数最多的就是预测值，那么这里运用了，numpy的argmax与bincount，首先通过bincount计算出数组中索引出现的次数，为什么要这么取？
因为我们在预测后，会有很多个label，而当我们取出距离前k个label，只需要统计在这k个label中计算每个label的次数，然后直接再通过argmax取出出现次数最多的就是最后的预测结果！
实例：
假设最后的label只有三类，分别是0，1，2，我们用一个array模拟
x = np.array([0,1,2,2,1,1])
通过bincount计算出每个label的次数！
np.bincount(x)
输出：
array([1, 3, 2], dtype=int64)
0出现1次，1出现3次，2出现2次，那么再通过argmax可以求出最多次数的label
np.argmax(np.bincount(x))
输出：
1
可以得到最后的预测label为1。也就是我们进行投票的结果，上述模拟的array就是我们的前k个最大值，类比过去，就好理解了！
一层循环
一层循环，直接使用矩阵切片来完成，
def compute_distances_one_loop(self, X):
# 500
num_test = X.shape[0]
# 5000
num_train = self.X_train.shape[0]
# (500,5000)
dists = np.zeros((num_test, num_train))
for i in range(num_test):
dists[i, :] = np.sqrt(np.sum(np.square(self.X_train - X[i, :]), axis=1))
return dists
X_train为(5000,3072)，而X为(500,3072)，对比维度
维度: 0 1
self.X_train 5000 3072
X 500 3072
根据broadcast机制，其中一个维度必须为1才可以满足broadcast的兼容性，那么将0维变为1即可，怎么变？
每次取X的当前行，也就是shape=(1,3072)，这里就用到了numpy的broadcast机制。
就是上述，循环500次，每次取X一行，上述维度对比：
维度: 0 1
self.X_train 5000 3072
X[i,:] 1 3072
那么此时就可以满足self.X_train与X[i,:]相减，此时得到的shape为(5000,3072)，然后axis=1，按照行求和，得到shape(5000,)，针对这个我这里用一个小例子验证：
t = np.sum([[0,1,2],[2,1,3]],axis=1)
t.shape
输出：
(2,)
对应的dists的shape为(500,5000)，那么将上述每一行赋值给dists每一行即可完成一层循环操作！
零层循环
转化为公式：
def compute_distances_no_loops(self, X):
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
dists = np.sqrt(np.sum(X**2, axis=1, keepdims=True) + (-2 * np.dot(X, self.X_train.T)) + np.sum(self.X_train**2, axis=1))
return dists
上述keepdims=True解释如下：
保持维度特性!!!
实例：
无keepdims参数加法：
np.sum(a**2,axis=1)
输出：
array([ 5, 25], dtype=int32)
会发现这个shape为(2,)，跟原来的数组的维度不一样，那么如何保持原有维度？
这就需要加上keepdims参数!
np.sum(a**2,axis=1,keepdims=True)
输出：
array([[ 5],
[25]], dtype=int32)
同理，本题也是如此，保持了500行1列的维度，然后进行矩阵运算，而后面self.X_train没有用到keepdims参数，为什么？
我们想要得到的是(500,5000)，而对于x^2与-2xy得到的分别是(500,1)与(500,5000)的shape，根据broadcast机制，直接可以进行加法，而后面那个如果加上keepdims参数，shape变为(5000,1)后，对比维度：
维度: 0 1
x^2-2xy 500 5000
self.X_train^2 5000 1
此时，第0个维度，无法进行加法，所以不能使用keepdims参数！！！
如果不加keepdims，self,.X_train^2直接是一维的数组，那么直接可以对行进行扩展成500，列保持5000，最终shape为(500,5000)，也就完成了零层循环！
最后，np.square与**都是对矩阵的每个元素平方，而如果要对矩阵进行平方，可以用a.dot(a)或者np.dot(a,a)，则是矩阵相乘！还有一个常用的是np.multiply(a,a)，与上述square以及**结果一致！
交叉验证
设置超参数k为5，然后通过交叉验证寻找最佳k!
代码提示用np.array_split分割，下面给出实例：
x = np.arange(6)
np.array_split(x,3,axis=0)
输出：
[array([0, 1]), array([2, 3]), array([4, 5])]
对array进行切分！
将训练集与测试集进行按照5折进行切分！
X_train_folds = np.array_split(X_train, num_folds, axis=0) # list
y_train_folds = np.array_split(y_train, num_folds, axis=0) # list
循环5次，设置将第1个array设置为验证集，后4个设置为训练集，训练集通过np.concatenate进行纵向合并！
这里参考网上大佬的代码，下面来解释一下，主要是里面的swap data，这里截一张k折图，每次将当前的fold作业一个验证集，而在这里通过交换验证集的数据，将验证集的数据交换到fold1位置，这样便于处理！
后面便是通过选择k来进行模型训练，寻找最佳k即可！
# num_folds = 5
for i in range(num_folds):
# train / validation split (80% 20%)
X_train_batch = np.concatenate(X_train_folds[1:num_folds])
y_train_batch = np.concatenate(y_train_folds[1:num_folds])
X_valid_batch = X_train_folds[0]
y_valid_batch = y_train_folds[0]
# swap data (for next iteration)
if i < num_folds - 1:
tmp = X_train_folds[0]
X_train_folds[0] = X_train_folds[i+1]
X_train_folds[i+1] = tmp
tmp = y_train_folds[0]
y_train_folds[0] = y_train_folds[i+1]
y_train_folds[i+1] = tmp
# train model
model = KNearestNeighbor()
model.train(X_train_batch, y_train_batch)
dists = model.compute_distances_no_loops(X_valid_batch)
# compute accuracy for each k
for k in k_choices:
y_valid_pred = model.predict_labels(dists, k=k)
# compute validation accuracy
num_correct = np.sum(y_valid_pred == y_valid_batch)
accuracy = float(num_correct) / y_valid_batch.shape[0]
# accumulate accuracy into dictionary
if i == 0:
k_to_accuracies[k] = []
k_to_accuracies[k].append(accuracy)
2.SVM
数据预处理
数据shape，同上！
Training data shape: (49000, 3072)
Validation data shape: (1000, 3072)
Test data shape: (1000, 3072)
dev data shape: (500, 3072)
下面接着就是让训练集与测试集都减去减去图像的平均值！
np.hstack水平扩展
X_train = np.hstack([X_train, np.ones((X_train.shape[0], 1))])
将训练集，水平扩展(X_train.shape[0], 1)，最终shape(49000,3073)
svm native
X是矩阵，W是权重(Wi表示每一类别权重)
X表示如下：
求梯度过程：
（6）式中wjxi表示第j个类别的得分！
Li表示(3)式中的每一行loss，Li的梯度写成如7所示的列向量，将每一行的loss分成每一个元素的loss，即公式(7)。
将Li的梯度分成最小的求Lij梯度！
对应的额代码，如下：
def svm_loss_naive(W, X, y, reg):
# C
num_classes = W.shape[1]
# N
num_train = X.shape[0]
loss = 0.0
for i in range(num_train):
# Li 每一行，对应(3)式
scores = X[i].dot(W)
# scores[y[i]] WyjXi 真正lable得分
correct_class_score = scores[y[i]]
# 每一列
for j in range(num_classes):
# j=y[i]不能求和，跳过
if j == y[i]:
continue
# Lij 对应(6)式中的每一个Lij
margin = scores[j] - correct_class_score + 1 # note delta = 1
# score>0
if margin > 0:
# 对应(6)式求和
loss += margin
# 对应(10)式
dW[:, y[i]] += -X[i, :]
# 对应(9)式
dW[:, j] += X[i, :]
有关svm及softmax后面继谈！
3.作者的话
如果您觉得本公众号对您有帮助，欢迎关注及转发，更多内容关注本公众号深度学习！