基因表达式编程——GEP
近年来,一些新的研究方法,如蚁群算法、人工神经网络、细胞自动机、人工免疫算法、进化算法等,它们通过模拟某一自然现象或过程(“拟物”或“仿生”)来求得问题解决的办法,具有高度并行与自组织、自适应和自学习等特征,已经在人工智能、机器学习、数据挖掘等领域中显示出强大的生命力与进一步发展的潜力。
在论文 基因表达式编程理论及其监督及其学习模型研究- 张克俊 中 提到:
通过构造独特的适应值函数和交叉验证方法来获得算法提前终止的条件,相关实验究证明,采用改进的基因表达式编程算法比基本基因表达式编程算法和其它机器学习方法所构建的监督机器学习模型在噪声数据处理能力和泛化能力上有明显的提高
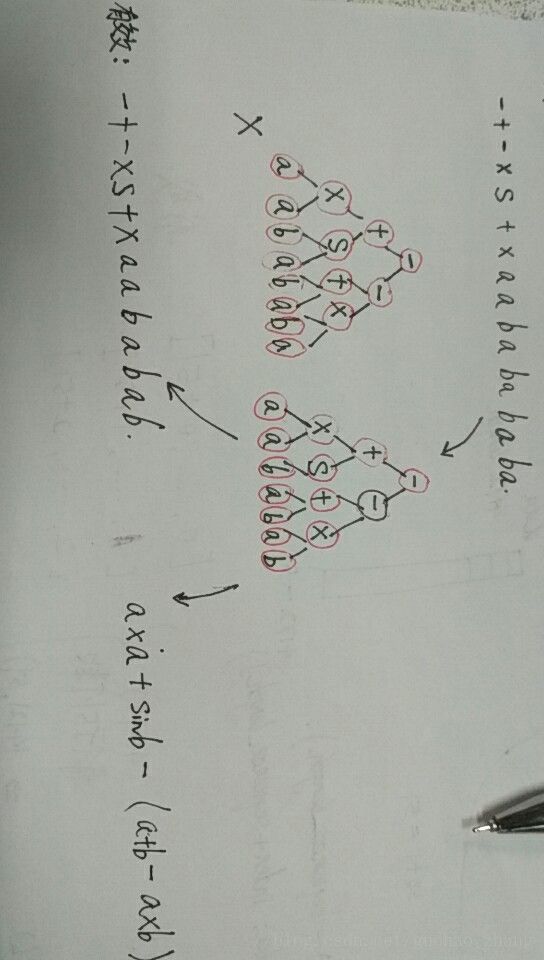
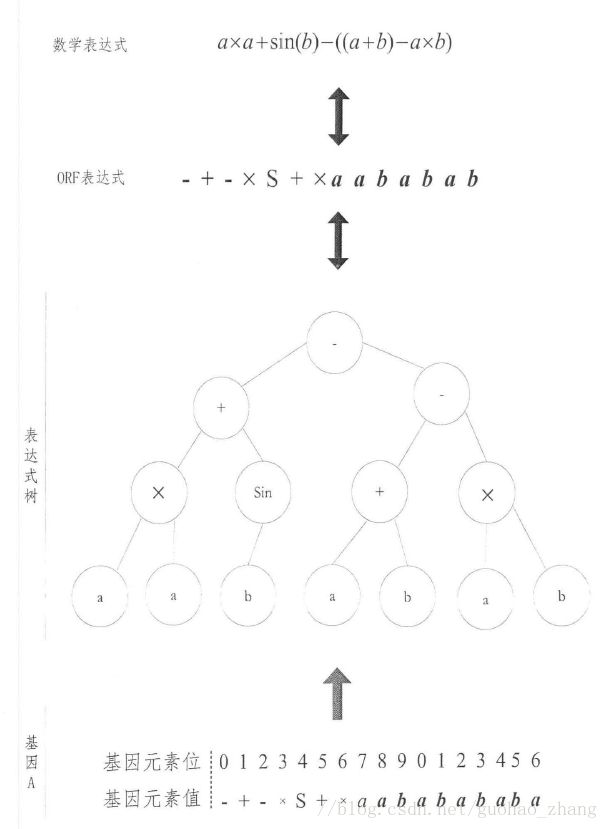
GEP在解码时,按照从左到右的顺序读取基因中的一个个字符,然后根据语法规则将基因映射为相应的表达式树。
GEP 的这种染色体结构兼备了GA 和GP 的个体组织方法的优点,因此在解决很多问题上,GEP 的效率远远要高于GA 和GP。
基因表达式编程在监督机器学习中的应用研究成果表明,其非常适合于解决分类、复杂函数关系发现问题

种群:由多个等长的个体组成;
个体:(染色体),包含一个以上的等长基因;
基因:头部 + 尾部
- 头部:终结符集T+ 函数符集F( +、-、*、/、%、sin、cos、tan、max、min、与、或、非、等等)
- 尾部:终结符集F (GEP输入、常量、变量 等等)
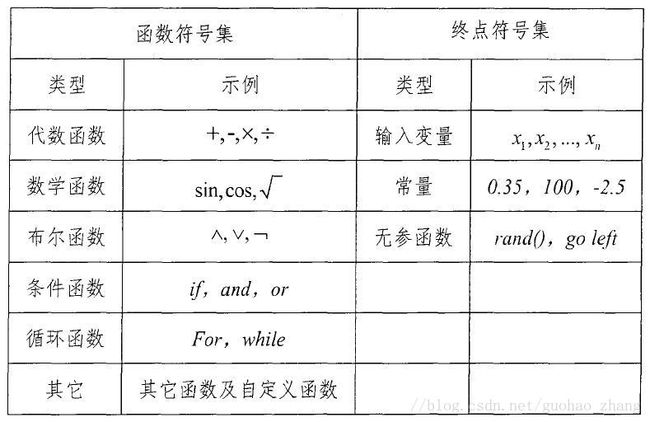
基因中的函数符号集:通常根据欲求解的问题来定义,可以直接取用标准函数,也可以使用自定义的函数。如对于一个
简单代数问题,可设 F={+,-,*,/},若是一个逻辑推理问题,可设 F={与, 或, 非};终点符号集则由数值常量、待求变量和无参函数构成。详细的函数符号集和终点符号集选取问题。
(1)基因编码
基因头部长度 h h 通常根据问题的复杂度来定义,尾部长度 t t : t=h∗(n−1)+1 t = h ∗ ( n − 1 ) + 1
其中 n 是 所有函数中最大的目数。基因头和基因尾部长度保持这样的关系,可以保证产生基因(编码)都是合法的。
(2)基因解码
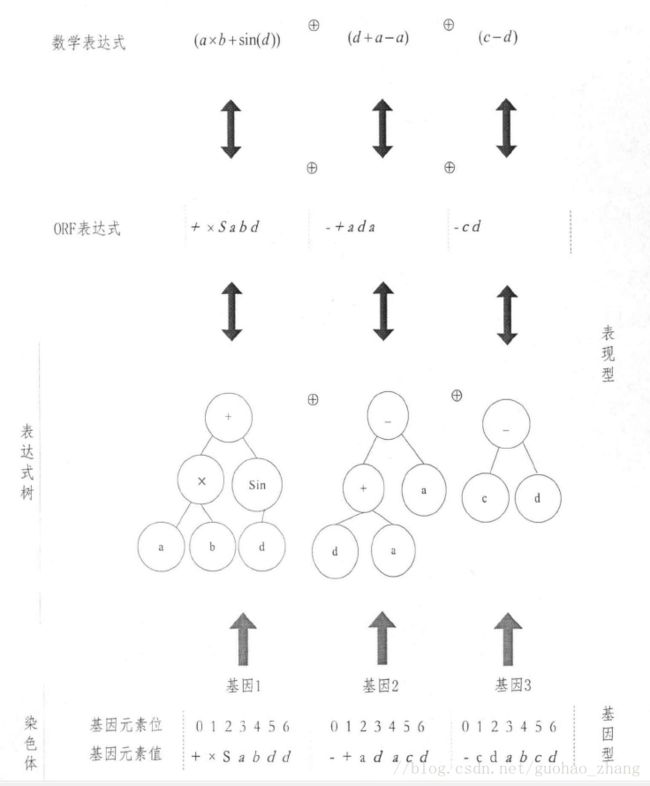
染色体
有一个以上的基因组成,基因之间用连接符 “⊕” 连接,连接符具体取值视情况而定,一般取 “ +,-,*,/ ”。
一个由个基因组成的染色体解码为表达式树并转化为盯表达式和数学表达式的过程:
基本中的遗传算子,主要包括选择、复制、变异、转座和重组,通常它们顺次执行,但变异、转座、重组之间操作的顺序,对最终结果并不十分重要。
选择算子
基本的选择算子是轮盘赌选择法。在轮盘赌选择中,每个个体的适应值在群体中所占的比例对应圆形赌盘的面积块,轮盘按种群大小进行相应次数的旋转(使得群体的大小不变),每次旋转只选择一个个体,个体的适应值越优,它被复制到下一代的可能性越大。
变异算子这里需要提的一点就是,为了让染色体的组织结构保持完整,避免非法个体产生,对变异方式进行了一定的限制,如基因头部的基因元素值可以变异成任何基因元素,而基因尾部的基因元素值,只能变异成终点符号集元素,因此,GEP的变异操作产生的新生个体都是合法的个体。这与遗传编程的变异操作会产生非法个体有明显的不同。
转座和重组就先不提及了,我现在需要快点捋过一遍GEP,见谅。
适应值函数
形式化表示:
在 浙江大学博士学位论文《基因表达式编程理论及其监督机器学习模型研究》中写到关于 GEP的形式化表示:









算法设计步骤:
这里需要留意的就是,
- 样本数据中有几个输入数据,终点符号集就包含几个变量。
确定选择策略:优胜劣汰是进化算法选择策略的核心思想,GEP中用到的选择策略主要有轮盘赌和锦标赛选择方法
轮盘赌算法:
轮盘赌选择方法,轮盘赌选择又称比例选择算子,其基本思想是:各个个体被选中的概率与其适应度函数值大小成正比。
设种群个体大小为 N N ,个体 xi x i 的适应度为 f(xi) f ( x i ) ,则个体 xi x i 的选择概率为:
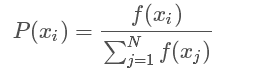
轮盘赌选择法可用如下过程模拟来实现:
(1) 在 [0,1] [ 0 , 1 ] 内产生一个均匀分布的随机数 r r 。
(2) 若 r≤q1 r ≤ q 1 ,则染色体 x1 x 1 被选中。
(3)若 qk−1<r≤qk(2≤k≤N) q k − 1 < r ≤ q k ( 2 ≤ k ≤ N ) , 则染色体 xk x k 被选中。
其中的 qi q i 称为染色体 xi(i=1,2,…,N) x i ( i = 1 , 2 , … , N ) 的积累概率, 其计算公式如下图所示:
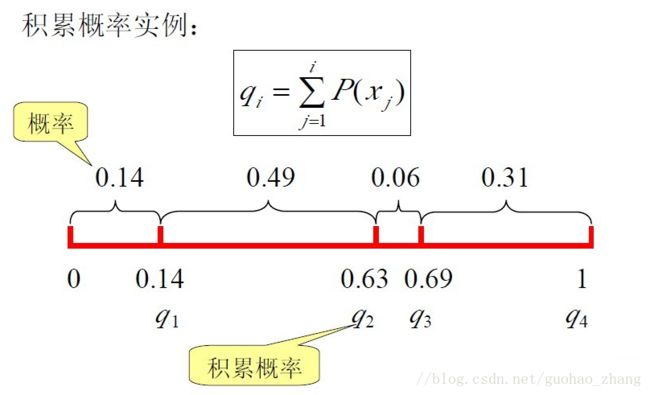
如何产生下一代:
(看了好久终于理清楚了,应该没有理解错吧)
首先,精英保留就是在使用遗传算子之前选出适应度值最大的个体,直接遗传到下一代,不对其进行遗传操作。目的是保留最好的各面,避免遗传算子破坏其优良特性。
19页
【未完……】