目标跟踪学习算法之二：DSST

版权声明：本文为博主原创文章，未经博主允许不得转载。

简介

       DSST(Accurate Scale Estimation for Robust Visual Tracking)在2014年VOT上夺得了第一名，算法简洁，性能优异，并且我上一篇所述的KCF夺得了第三名，两者都是基于滤波器的算法，这一年是CF义军突起的一年，值得研究这些相近的优秀算法。这篇算法是基于MOSSE的改进，突出内容是加入了尺度变换，下面开始逐一讲解算法内容。

相关滤波器

　　首先讲一下MOSSE提出的相关滤波器，从目标中提取一系列的图像patches,记为 f1,f2,...ft 作为训练样本，其对应的滤波器响应值为一个个高斯函数 g1,g2,...gt ,而目的就是找到满足最小均方差(Minimum Output Sum of Squared Error)的最优滤波器：

ε=∑j=1t||ht∗fj−gj||2=1MN||HtFj−Gj||2(1)

其中第二个等号根据Parseval定理导出，等式左侧是空域的方程式，右侧是频域的方程式，正正是这个等式，使得我们将问题求解变换到频域里求解， ε 的最小值在频域里的解如下：

Ht=∑tj=1GjFj∑tj=1FjFj(2)

一般而言， gj 可以是任意形状的输出，这里的输出 gj 是高斯型的函数，峰值位于中心处。这个方法的 技巧或者 目的在于：一是运算简洁，基本都是矩阵运算；二是引入快速傅里叶(FFT)大大加快运算效率。这即是相关滤波器被应用在Tracking并获得较好效果的原因，满足了对速度的一大需求。
在得到上述相关滤波器后，对于新的一帧中的候选输入样本z,求相关得分y：

y=F−1(HtZ)(3)

y取最大响应值时对应的位置z为新的目标位置。

算法思想

　　算法设计了两个一致的相关滤波器，分别实现目标的跟踪和尺度变换，定义为位置滤波器(translation filter)和尺度滤波器(scale filter),前者进行当前帧目标的定位，后者进行当前帧目标尺度的估计。两个滤波器是相对独立的，从而可以选择不同的特征种类和特征计算方式来训练和测试。文中指出该算法亮点是尺度估计的方法可以移植到任意算法中去。

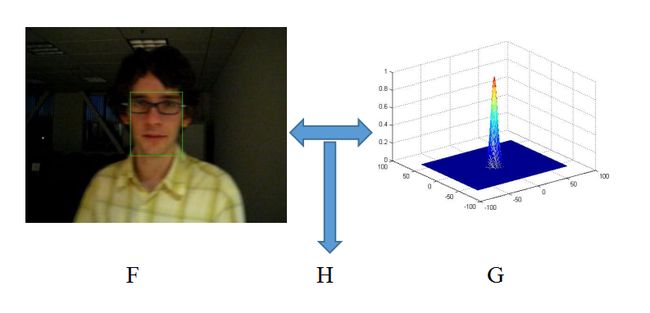
算法流程：如上图所示，通过左侧的图像patch目标提取的特征F和右侧的高斯型函数G，应用式(2)得到一个相关滤波器H。然后在下一帧将测试的图像patches提取特征Z作为输入，与相关滤波器H按照式(3)进行运算，得到响应值y最大的候选目标，所以算法很简洁。
该算法将输入信号 f (图像中的某一个patch)设计为d维特征向量(可选gray,hog)，通过建立最小化代价函数构造最优相关滤波器 h ,如下：

ε=||∑l=1dhl∗fl−g||2+λ∑l=1d||hl||2(4)

其中， l 表示特征的某一维度， λ 是正则项系数，作用是消除 f 频谱中的零频分量的影响，避免上式解的分子为零，如下：

Hl=G¯¯¯Fl∑dk=1Fk¯¯¯¯Fk+λ=AltBt(5)

由于patch中的每个像素点需要求解 d x d 维的线性方程，计算非常耗时，为了得到鲁棒的近似结果，对上式中分子 Alt 和分母 Bt 分别进行更新:

Alt=(1−η)Alt−1+ηGt¯¯¯¯Flt

Bt=(1−η)Bt−1+η∑k=1dFkt¯¯¯¯Flt(6)

其中， η 为学习率。
在新的一帧中，目标位置可以通过求解最大相关滤波器响应值得到：

y=F−1⎧⎩⎨∑dl=1Al¯¯¯¯ZlB+λ⎫⎭⎬(7)

快速尺度空间跟踪

　　本算法的亮点就是提出的基于一维独立的相关滤波器的尺度搜索和目标估计方法。具体操作方法是：在新的一帧中，先利用2维的位置相关滤波器来确定目标的新候选位置，再利用1维的尺度相关滤波器以当前中心位置为中心点，获取不同尺度的候选patch，从而找到最匹配的尺度。尺寸选择原则是：

anP×anR,n∈{[−S−12],...[S−12]}(8)

其中， P,R 分别为目标在前一帧的宽高， a=1.02 为尺度因子， S=33 为尺度的数量。上述尺度不是线性关系，而是由精到粗(从内到外的方向)的检测过程。

算法流程

　　论文中的流程图已经详细写的挺详细了，为了保持内容完整性再赘述一遍：
Input:
输入图像patch It
上一帧的位置 Pt−1 和尺度 St−1
位置模型 Atranst−1、Btanst−1 和尺度模型 Ascalet−1、Bscalet−1
Output:
估计的目标位置 Pt 和尺度 St
更新位置 Atranst、Btranst 和尺度模型 Ascalet、Bscalet

其中,
位置评估：
1.参照模板在前一帧的位置，在当前帧中按照前一帧目标尺度的2倍大小提取一个样本 Ztrans
2.利用 Ztrans 和 Atranst−1、Btanst−1 ，根据公式(7)计算 ytrans
3.计算 max(ytrans) ，得到目标新的位置 Pt
尺度评估：
4.以目标当前新位置为中心，提取33种不同尺度的样本 Ztrans
5.利用 Ztrans 和 Atranst−1、Btanst−1 计算出 yscale
6.计算 max(yscale) ，得到目标准确的尺度 St

模型更新：
7.提取样本 ftrans 和 fscale
8.更新位置模型 Atranst 和 Btranst
9.更新尺度模型 Ascalet 和 Bscalet

下面给出两个不同相关滤波器的关键代码：
训练部分：

    %提取特征训练样本输入X
    %样本中每个像素点计算28维融合特征(1维原始灰度+27维fhog)
    %乘以二维hann后作为输入X
    %提取特征用于位置相关滤波器
    xl = get_translation_sample(im, pos, sz, currentScaleFactor, cos_window);

    %获取分子A=GF;分母B=F*F;此时没有lambda
    xlf = fft2(xl);
    new_hf_num = bsxfun(@times, yf, conj(xlf));
    new_hf_den = sum(xlf .* conj(xlf), 3);

    %把每个样本resize成固定大小，分别提取31维fhog特征，每个样本的所有fhog再
    %串联成一个特征向量构成33层金字塔特征，乘以一维hann窗后作为输入X
    % 提取特征用于尺度相关滤波器
    xs = get_scale_sample(im, pos, base_target_sz, currentScaleFactor * scaleFactors, scale_window, scale_model_sz);

    %同样的获取分子A=GF;分母B=F*F;此时没有lambda
    xsf = fft(xs,[],2);
    new_sf_num = bsxfun(@times, ysf, conj(xsf));
    new_sf_den = sum(xsf .* conj(xsf), 1);

检测部分：

         %提取特征测试输入F
         %样本中每个像素点计算28维融合特征(1维原始灰度+27维fhog)
         %乘以二维hann后作为输入F
         %用于位置相关滤波器
         xt = get_translation_sample(im, pos, sz, currentScaleFactor, cos_window);

        %计算响应值y=F-1{(A*Z)/(B+lambda)}
        xtf = fft2(xt);
        response = real(ifft2(sum(hf_num .* xtf, 3) ./ (hf_den + lambda)));

        %找到max(y)得到目标新位置
        [row, col] = find(response == max(response(:)), 1);

        % 更新目标位置
        pos = pos + round((-sz/2 + [row, col]) * currentScaleFactor);

        %把每个样本resize成固定大小，分别提取31维fhog特征，每个样本的所有fhog再
        %串联成一个特征向量构成33层金字塔特征，乘以一维hann窗后作为输入F
        % 用于尺度相关滤波器
        xs = get_scale_sample(im, pos, base_target_sz, currentScaleFactor * scaleFactors, scale_window, scale_model_sz);

        %得到尺度变换的响应最大值y=F-1{(A*Z)/(B+lambda)}
        xsf = fft(xs,[],2);
        scale_response = real(ifft(sum(sf_num .* xsf, 1) ./ (sf_den + lambda)));

        %找到max(y)得到当前的尺度
        recovered_scale = find(scale_response == max(scale_response(:)), 1);

        % 更新当前尺度
        currentScaleFactor = currentScaleFactor * scaleFactors(recovered_scale);
        if currentScaleFactor < min_scale_factor
            currentScaleFactor = min_scale_factor;
        elseif currentScaleFactor > max_scale_factor
            currentScaleFactor = max_scale_factor;
        end

总结

　　DSST算法是一个非常典型且高效的基于相关滤波器的目标跟踪算法，非常值得学习和借鉴其中的思想和方法，尽管跟踪算法迭代很快，在15年的VOT上被深度学习的算法所取代，但是仍然有不少算法基于相关滤波器进行改进，所以学习这类算法是相当有益的。