【Libra R-CNN: Towards Balanced Learning for Object Detection】--- 对象检测阅读笔记
论文名称:Libra R-CNN: Towards Balanced Learning for Object Detection
论文作者:Jiangmiao Pang, Kai Chen, Jianping Shi, Huajun Feng, Wanli Ouyang, Dahua Lin
发行时间:Submitted on 4 Apr 2019
论文地址:https://arxiv.org/abs/1904.02701v1#
代码开源:https://github.com/open-mmlab/mmdetection
- 一. 前言
- 二. Libra R-CNN Model
- 1. Balanced IoU sampling
- 2. Balanced feature pyramid
- a. 详细过程
- b. Integrate过程解释
- c. Refine过程解释
- 3. Balanced L1 loss
- 三. 实验结果
- 四. 总结
一. 前言
在检测过程中,作者对在CNN中连续卷积不同尺寸的feature map划分成三个层次:sample level, feature level, objective level. 并提出 Libra R-CNN 来对object detection也就是上面三个level进行平衡。其中, Libra R-CNN 集称了三个部件:
- IoU-balanced sampling
- 用于减少样本数(sample)
- balanced feature pyramid
- 用于减少特征数(feature)
- balanced L1 loss
- 用于减少目标水平的不平衡(objective level)
Libra R-CNN在没有bells和whistles的情况下,在MSCOCO上分别比FPN和RetinaNet在AP(平均精度)上提高了2.5和2.0 points
二. Libra R-CNN Model
作者将本文的检测模型分为了三个阶段:
- sample level
- 用于得到image中描绘出object的候选框框
- feature level
- 将不同尺寸的特征金字塔进行特征融合
- objective level
- 用于将image中的对象分类和定位
对于Libra R-CNN,作者一共构建了三个组件:
- IoU-balanced sampling
- balanced feature pyramid
- balanced L1 loss
1. Balanced IoU sampling
对于一般的random sampling(从M个候选框中选出N个Negative样本),对每个样本的选择概率是 p = N M p= \frac{N}{M} p=MN
而通过实验发现hard和sample的分布不均衡,而作者提出 IoU-balanced sampling 的方法来提高hard negatives的选择概率,即通过将采样间隔均分成K个批次,然后每次从这些批次中均匀的选择样本(从M个候选框中选出N个Negative样本,并分成K个批次) p k = N K ∗ 1 M k , k ∈ [ 0 , K ) , p_k=\frac{N}{K}*\frac{1}{M_k},k\in [0,K), pk=KN∗Mk1,k∈[0,K),
其中,
- M k M_k Mk是在对应的分成的K个批次的一次中的抽取的候选框的数量
- K K K是均分成的批次,本实验默认 K K K为 3 3 3
2. Balanced feature pyramid
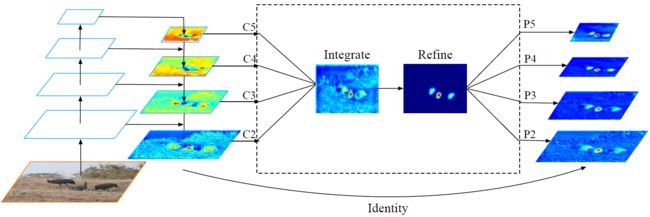
作者提出,首先由FPN对image提取处4种不同尺度的feature { C 1 , C 2 , C 3 , C 4 } \left \{C_1,C_2,C_3,C_4\right \} {C1,C2,C3,C4}, 然后对这四种size的feature进行rescale操作到同一尺度的feature:上采样和下采样(线性插值和池化操作),最后再对之进行一个Refine操作,得到不同尺度的feature { P 1 , P 2 , P 3 , P 4 } \left \{P_1,P_2,P_3,P_4\right \} {P1,P2,P3,P4},过程如下图所示:
a. 详细过程
- 输入image,由FPN得到不同尺度的feature { C 1 , C 2 , C 3 , C 4 } \left \{C_1,C_2,C_3,C_4\right \} {C1,C2,C3,C4}
- 执行Integrate操作得到平均了的一个feature C C C
- 执行Refine操作得到和之前各层的相同尺寸4个的feature { P 2 , P 3 , P 4 , P 5 } \left \{P_2,P_3,P_4,P_5\right \} {P2,P3,P4,P5}用于后面的对象检测
b. Integrate过程解释
- 通过上采样(插值)和下采样(Pool)将上述四个不同size的feature转换到同一尺度
- 对这四个同一size的feature执行取平均的操作得到平均的feature C = 1 L ∑ l = l m i n l m a x C l C=\frac{1}{L} \sum^{l_{max}}_{l=l_{min}} C_l C=L1l=lmin∑lmaxCl
c. Refine过程解释
将AVG的feature经过 non-local network 或者 conv 再次得到和之前各层的相同尺寸4个的feature { P 2 , P 3 , P 4 , P 5 } \left \{P_2,P_3,P_4,P_5\right \} {P2,P3,P4,P5}
Non-local network 与 Conv操作相比,差别不大,但是 Non-local network 要更加稳定
3. Balanced L1 loss
首先定义两名词:
- outliers:sample(采样)到的loss(损失)大于等于1的样本,可视为 hard sample,不易于训练
- inliers:sample(采样)到的loss(损失)小于1的样本,可视为 easy sample,对训练较友好
作者通过实验发现,在train过程中,较少的outliers却贡献了 70 % 70\% 70%的梯度,而较多的inliers却只贡献了 30 % 30\% 30%的梯度,需要采取某种措施来让loss的计算更加均衡:
重新定义L1 loss梯度,记为 L b L_b Lb:
∂ L b ∂ x = { α l n ( b ∣ x ∣ + 1 ) ) i f ∣ x ∣ < 1 γ o t h e r w i s e \frac{\partial L_b}{\partial x}=\left\{\begin{matrix} \alpha ln(b \left | x \right | + 1)) & if \left | x \right | < 1 & \\ \gamma & otherwise & \end{matrix}\right. ∂x∂Lb={αln(b∣x∣+1))γif∣x∣<1otherwise
即对 ∣ x ∣ < 1 \left | x \right | < 1 ∣x∣<1 的梯度进行了替换,通过
- α \alpha α 来使得 inliers 获得更多的梯度,本实验设置 α \alpha α为0.5
- γ \gamma γ 通过整体放大来来调整回归误差的上界,使得目标函数更好地平衡参与的任务, 本实验设置 γ \gamma γ为1.5
- b b b 则用于平衡 α \alpha α 和 γ \gamma γ ,它们需要满足该式子: a l n ( b + 1 ) = γ aln(b+1) = \gamma aln(b+1)=γ
对上述梯度进行积分,得到 L1 loss function:
L b ( x ) { α b ( b ∣ x ∣ ) l n ( b ∣ x ∣ ) + 1 i f ∣ x ∣ < 1 γ ∣ x ∣ + C o t h e r w i s e L_b(x) \left\{\begin{matrix} \frac{\alpha}{b}(b \left | x \right |)ln(b \left | x \right |)+1 & if \left | x \right | < 1& \\ \gamma \left | x \right | + C & otherwise & \end{matrix}\right. Lb(x){bα(b∣x∣)ln(b∣x∣)+1γ∣x∣+Cif∣x∣<1otherwise
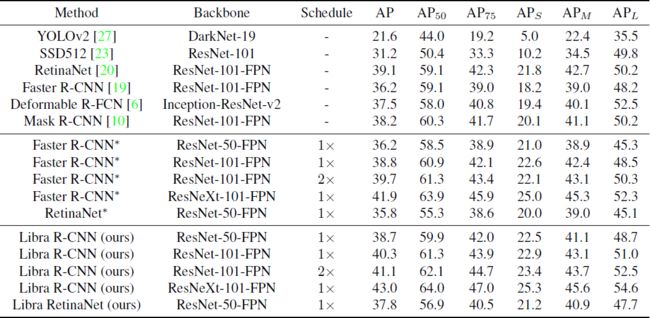
三. 实验结果
可见提升效果还是挺大的
四. 总结
作者提出 balanced 概念,并将这个概念分别应用到IoU检测候选框、特征融合、损失计算这三个方面上,效果显著提升,值得一读