隐马尔科夫(HMM)模型

隐马尔科夫(HMM)模型

隐马尔科夫(Hidden Markov model)模型是一类基于概率统计的模型，是一种结构最简单的动态贝叶斯网，是一种重要的有向图模型。自上世纪80年代发展起来，在时序数据建模，例如：语音识别、文字识别、自然语言处理等领域广泛应用。隐马尔科夫模型涉及的变量、参数众多，应用也很广泛，以至于很多人不明白模型到底在做什么，模型能够做什么。

HMM中hidden&Markov

首先需要明确的是什么是马尔科夫性质。假设随机过程中某一时刻的状态 st s t 的概率分布满足：

p(st|st−1,st−2,...,s0)=p(st|st−1) p ( s t | s t − 1 , s t − 2 , . . . , s 0 ) = p ( s t | s t − 1 )

通俗的说就是，随机过程中某一时刻的状态 st s t ，只与它前一时刻的状态 st−1 s t − 1 有关，以上就是马尔科夫性质。我们知道自然世界中的很多现象都不符合这一性质，但是我们可以假设其具有马尔科夫性质，这为原来很多无章可循的问题提供了一种解法。
如果某一随机过程满足马尔科夫性质，则称这一过程为马尔科夫过程，或称马尔科夫链。

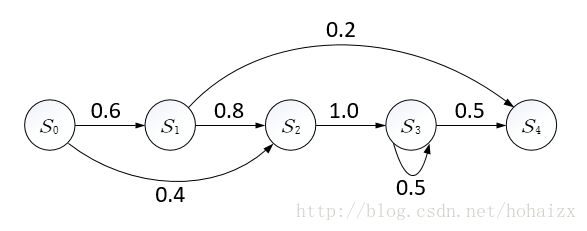
在马尔科夫链中，每一个圆圈代表相应时刻的状态，有向边代表了可能的状态转移，权值表示状态转移概率。
那HMM中的隐体现在哪呢？这里“隐”指的是马尔科夫链中任意时刻的状态变量不可见，也就是说状态序列 s0,s1,...,st s 0 , s 1 , . . . , s t 无法直接观测到。但是HMM中每时刻有一个可见的观测值 ot o t 与之对应，而且 ot o t 有且仅于当前时刻隐状态 st s t 有关， st s t 外化表现为 ot o t 的概率称为输出概率，因此隐马尔科夫模型的结构图如下所示。

因此隐马尔科夫模型中马尔科夫链指的是隐状态 s0,s1,...,st s 0 , s 1 , . . . , s t 序列。

HMM之掷骰子

上面的定义虽然给出了隐马尔科夫模型的书面表达，但是对于隐马尔科夫模型的隐状态、观测值、转移概率、输出概率我们依然没有一个直观的概念。下面将采用掷骰子的例子，将隐马尔科夫模型的各种概念和例子中的变量联系起来。
我们假设一个赌场里来了一个老千，他带有两种作弊骰子，分别记为骰子2，骰子3，骰子2掷出较小点数的概率较大，骰子3掷出较大点数的概率更大。所以现在我们有三种骰子，分别是赌场正常骰子1，和两种作弊骰子2，骰子3。这就是三种隐状态，因为我们不知道老千每次使用的是哪种骰子。但是我们知道老千切换骰子的习惯，可以表示如下图：

这个概率就是转移概率，表明了隐状态从一种状态转换到另一种状态的概率，可以写成矩阵的形式：

A=⎛⎝⎜0.150.300.200.450.200.500.400.500.30⎞⎠⎟ A = ( 0.15 0.45 0.40 0.30 0.20 0.50 0.20 0.50 0.30 )

我们也知道三种骰子掷出1~6点的概率分别如下：

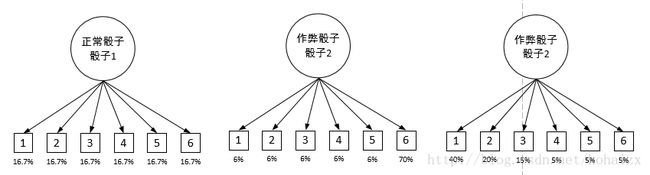
这些概率就称作输出概率，因为这个概率表明了从某种骰子(隐变量)到骰子点数(可观测值)的概率。输出概率也可以用矩阵的形式表示如下：

B=⎛⎝⎜0.160.060.400.160.060.200.160.060.150.160.060.050.160.060.050.160.700.05⎞⎠⎟ B = ( 0.16 0.16 0.16 0.16 0.16 0.16 0.06 0.06 0.06 0.06 0.06 0.70 0.40 0.20 0.15 0.05 0.05 0.05 )

以上转移概率矩阵和输出概率矩阵就囊括了整个HMM模型，这个模型描述了状态转移的所有可能以及概率，也表明了状态改变带来的外在表现的呈现以及概率。
因此，用一句话总结HMM模型就是：有一个随时间不断改变的隐藏状态，它持续影响系统的外在表现。

HMM模型五元组

HMM模型可以用五元组( O,S,A,B,Π O , S , A , B , Π )表示。其中

• O:{o0,o1,...,0n} O : { o 0 , o 1 , . . . , 0 n } 表示观测系列，是系统的外在可观测变量。
• S:{s0,s1,...,sn} S : { s 0 , s 1 , . . . , s n } 表示隐状态序列，是导致系统外在表现变化的内因。
• A:{aij=p(sj|si)} A : { a i j = p ( s j | s i ) } 表示状态转移概率。
• B:{bij=p(oj|si)} B : { b i j = p ( o j | s i ) } 表示输出概率。
• Π:{π0,π1,...,πm} Π : { π 0 , π 1 , . . . , π m } ，表示初始状态概率分布。

HMM三类问题

根据以上HMM模型五元组表示，我们可以归纳出HMM模型解决的三类主要问题。

1、评估问题

已知状态转移矩阵 A A ，输出矩阵 B B ，和观测序列，求该观测序列出现的可能性。
这就是评估问题，最显而易见的一个应用就是异常检测，如果一个多次HMM模型实验的结果都显示观测序列出现的概率较小，说明观测序列和模型不太吻合，则可以断定系统可能出现了异常。该问题最简单粗暴的解法就是直接组合出所有的可能隐藏状态序列，然后求出每个隐藏状态序列导致观测序列发生的概率，最后将概率求和即是最终结果。但是列举出所有可能的状态序列是一个指数爆炸增长的问题，在实际系统中不太可能实现。因此有人提出了forward/Backward 算法。（具体算法后面分章节再介绍）

2、解码问题

已知状态转移矩阵 A A ，输出矩阵 B B ，和观测序列，找出最有可能产生该观测序列的隐藏状态序列。
这个问题通常被称作解码问题，该问题通常也被称作“由果溯因”。隐状态通常是导致系统外在表现变化的“内因”，观测序列只是隐状态变化带来的“结果”。最常见的应用就是语音识别，即将某一段语音转化成对应的文字序列。解决该问题也可以采用同问题一类似的枚举法，只需要将所有可能序列的概率求和改为找最大概率对应序列即可，但同样效率不高。因此解决此类问题常用Viterbi算法。（具体算法后面分章节再介绍）

3、学习问题

已知仅仅是很多观测序列，估计HMM模型的参数的可能取值。
这个问题被称作学习问题，通过大量的样本数据去学习最优的模型参数，该问题的求解比较复杂，常采用Baum-Welch算法。

本人目前正在学习机器学习和自然语言处理，第一次接触隐马尔科夫模型，难免有许多总结得不准确的地方，HMM模型涉及的内容也比较的多，以后将边学习边改进扩充该块内容，欢迎大家交流讨论！

参考文献

知乎【如何用简单易懂的例子解释隐马尔可夫模型？】