ML：图解Error = Bias^2 + Var + Irreducible Error

 

---

一、怎么举个例子理解误差公式的三个部分？

即误差Err /  偏差Bias / 方差Var / 不可避免的标准差之间，是什么关系？ 先上结论：  误差来源有三个：

1. Irreducible Error，即不可避免误差部分，刻画了当前任务任何算法所能达到的期望泛化误差的下限，即刻画了问题本身的难度；
2. Bias，即偏差部分，刻画了算法的拟合能力，Bias偏高表示预测函数与真实结果相差很大；
3. Variance，即方差部分，则代表 “同样大小的不同数据集训练出的模型” 与 “这些模型的期望输出值” 之间的差异。训练集变化导致性能变化，Var高表示模型很不稳定。

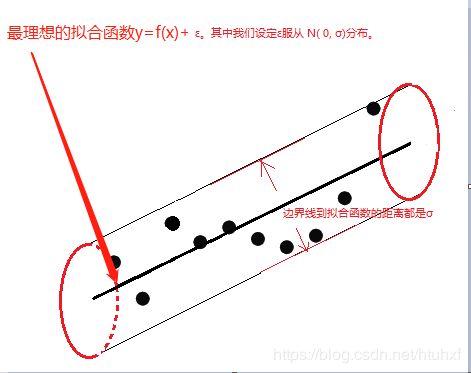
举个例子：假设我们手头有个数据集，不妨叫做y集，那么应该存在一条最理想的拟合函数，服从 。如图

1. irreducible Error：上图的例子中，它大小是，来自于最理想的拟合函数  和真实样本值之间，换句话说它是需要预测的“总体的离散度”——而它是Irreducible的。
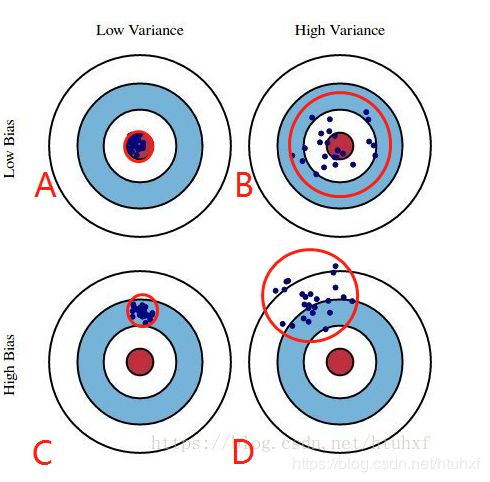
2. Bias和Var：见下图：即在上图的侧视图中、把样本分布区域缩小为靶，靶心点为最理想的拟合函数线，模型生成的N个结果为绿点（一个模型运行N次的N个结果，或N个模型运行一次的N个结果）。模拟结果有A/B/C/D四种（分布在红圈范围里）： 

          *  Bais：和 和 “的期望” 的离散程度；

          *  Var： 的N个结果的离散程度；

链接请点击：Understanding the Bias-Variance Tradeoff, 作者 Scott Fortmann-Roe.

现实中，这是因为我们的训练样本集，往往因为很多条件约束比如时间不够、y集太大等，小于总体样本，所以只能得到不那么理想的拟合函数。

拟合函数的打靶能力/拟合能力就有四种情况。

• 相对于理想的拟合曲线，即靶心圆来说：A结果最好，没有Var和Bias。
• B和C结果次之，分别没有Bias和Var部分。
• D结果最不好，但现实中最常见，Bias和Var都有。

---

二、怎么从数学角度理解误差公式？

误差来源公式：

1）误差来源公式简单推导。

2）误差公式的详细推导。

• 误差来源公式简单推导：

上式子来源于：

上式子来源于：

其中，真实值Y是因变量，X是自变量，。其中误差服从 。是的预估函数（通过线性回归或者其他模型算法得到的）。

• 误差公式的详细推导：

首先，我们知道；其次，因为函数是确定的（虽然未知&需要利用样本预估），所以；结合服从，可知：

                            (1)

                         (2)

 

                   带入，

                    带入（1）和（2）式子，

              

              

               

——证明完毕。