数据科学个人笔记：神经网络（网络结构+反向传播）

该篇主要是学习吴恩达老师的深度学习课程笔记，未完待续

 

一、待解决的问题

现在，我们有一堆样本，每个样本由一组输入值(向量x表示)和一组输出值(向量y表示，在我们举例的模型中y是一个1*1的向量)。我们要解决的问题，是通过这些已知了输入值x和输出值y的样本们，寻找出其中x和y的对应关系，之后我们就可以使用这种对应关系去构建模型，来判断那些只知道x值但不知道y值的样本，它们的y值是多少了。而这些已知了输入值和输出值的样本们，就是我们用来建模的数据了，我们可以将这些数据分为训练集、验证集和测试集。具体这些分类有什么用，我们之后进行讨论。

二、解决问题的模型

为了构建这样一个能通过输入一组x值计算出输出值y的模型，我们假设x和y之间的对应关系是以一个神经网络的形式存在的，即，我将一组输入值x放进一个神经网络的输入端（也就是神经网络的第0层），在神经网络的输出端（也就是第l层）就会输出一个y。

（一）关于神经网络，我们先明确以下几点

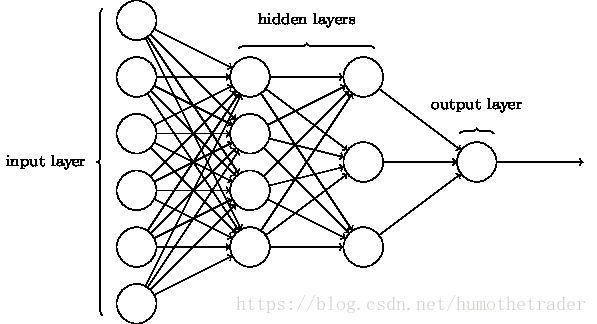
1.网络：什么是神经网络呢？它长成下面这个样子

2.层：一个神经网络，不包括最左边的输入端，当中的这几层我们称为隐藏层，最后一层我们称为输出端，隐藏层加上输出端的层数之和就是我们这个神经网络模型的层数l，l是多少，我们就称这个模型是多少层的神经网络（上图就是三层的神经网络）。

3.节点：如上图所示，每一层中有不同的节点，对第i层的节点数我们可以标记为m(i)。

（二）节点内部发生的计算

这些节点有什么用呢？其实这些节点每一个都是一个线性函数，如图我们可以看到每个节点都有好多箭头进入它，也有好多箭头从它里面出来。其实进入它的箭头就表示被输入这个节点（也就是输入这个线性函数）的x，从它里面出来的箭头就表示输入x后节点（线性函数）计算所得的y。通常我们输入线性函数的都是一组x（x1，x2，x3......），所以每个节点中也就要有一组权重参数w和一个常量参数b。什么意思呢？其实每个节点中的线性函数如下所示：

y=w1x1+w2x2+w3x3+。。。+w(n)x(n)+b

写成矩阵形式就是y=W’X+b

根据以上公式也就是说，每个节点是由一组参数（W,b）组成的，也就是n个w和1个b，共n+1个参数。每当一组x被输入一个节点后，这组参数所构成的函数就会计算出一个y值输出。我们可以标记第i层的第j个节点中的参数数量为n(ij)个。

但是事实上，每个节点中是不能只用一个线性函数输出一个y就ok了，由于某种原因，我们需要设置一个激活函数g(y)，然后在每个节点中，我们会将x输入以上n+1个参数构成的线性函数中，计算出一个y值，y值再输入激活函数g(y)中，计算出一个z值，这个z值才是每个节点最后输出的值，也就是那些从节点中出来的箭头。具体激活函数g的选取，不同的模型也各不相同，此处我们就先以g(y)来表示它（通常来说g(y)这个函数里是没有未知参数的，且每个节点中的激活函数个g(y)是相同的）。由此，每个节点中发生的事情可以用如下流程表示：

1.向节点中输入一组x； 

2.通过节点中当前的参数们W和b构成的线性函数，计算出一个y值； 

3.将y值输入激活函数g(y)中，计算出一个z值； 

4.将z值输出节点。

（三）层的运作原理

那这些层又有什么用呢？

现在，假设我们构建了一个l=4的神经网络（即四层神经网络），那么整个神经网络将会有5层，包括一个第0层输入层，第1、2、3层隐藏层，和第4层输出层。我们设每个输出层有三个节点，每个隐藏层都有四个节点，输出层有一个节点。

输入层和输出层的节点数是不能由我们自己随便设置的，要根据我们需要处理的样本的形式来。如果我们处理的样本，都是输入三个x，输出一个y的，那么输入层就必须是三个节点的，输出层就必须是一个节点的。而其中每个隐藏层的节点数，我们可以根据自己的建模的需要来自行设置。

现在我们要往模型里输入一个样本，将该样本的输入值（一组x）输入神经网络中，经过每一层各个节点的计算，最终在输出层输出一个y。那么，我们要怎么做呢？

首先，我们将这组x中的x1、x2、x3分别放在输入层（第0层）的三个节点上，于是输入层（第0层）会自动将三个值输入到下一层当中。怎么个输入法呢？根据图中所示，第0层中的每个输出量都会被作为输入量输入下一层（第1层）的每一个节点中。比如第0层的输出量是x1、x2、x3，则第1层的节点1的输入量就是x1、x2、x3，节点2的输入量也是x1、x2、x3，以此类推。当这些输入量被送进节点后，就会发生我在“节点内部发生的计算”那一章中描述的计算流程，每个节点也就会输出一个z值。若我们记第1层第一个节点的输出值为z1，第2、3、4个节点输出z2、z3、z4，则第2层第一个节点的输入值就是z1、z2、z3、z4，第2个节点的输入值也是这四个，以此类推。

由此，我们可以总结出，我们将样本的一组输入值x放入神经网络后，它会经过网络中每一层的计算。每一层每个节点会计算输出1个值，那么若这一层有4个节点的话，这一层总共就会输出由4个输出量组成的一组值，这组值会在输入下一层时，被重复作为下一层每一个节点的输入值，就这样一层一层往后推，最终在输入端（第l层）计算出一个输出量y值。

（四）构建损失函数

根据我们上面描述的模型，若我们当前有20个样本，这些样本都已知了输入量x=（x1，x2，x3）和输出量y，我们要怎样做才能构建出x与y之间的关系，从而在我们遇到新的样本时，能够通过样本的x来计算出y呢？

其实原理非常简单。首先我们来看上几章所描述的这个神经网络模型，它虽然看起来很复杂，但是实际上在层数和节点数以及所有节点的激活函数确定的情况下，随便输入任一个样本的x进入模型，输入的y是多少只取决于神经网络中各节点内这些参数的值是多少。如果将模型中所有节点的参数设为一个集合的话，我们可以用C(W,b)来表示它，也就是说，要找出x和y之间的关系，就等于是要找出一组C(W,b)的参数，使得每组x输入模型后，用这组参数计算出来的y每次都能等于样本本身已知的真实y值。

若设每个样本的x输入模型后输出的量为y*，每个样本真实的输出值为y，则我们要解决的就是以下这个一个优化问题：

模型的参数集合C(W,b)选取何值时，能够使得所有样本的模型输出量y*和真实输出值y之间的平方差达到最小，及取到min(sum((y-y*)^2))。

这里的L=sum((y-y*)^2)就是模型的损失函数。这个L取到最小值时，我们认为此时的模型和其中的参数最大程度地满足了我们的需求——能通过输入样本的x来计算出与样本真实y值偏差尽量小的y*值。

（五）基于求偏导的梯度下降算法

由于y*=f(C(W,b))，也就是说每一个y*是由这些参数C(W,b)和我们输出的每个样本的x来计算得出的，而x是常数，所以计算y*的式子中唯一的变量就是这些参数C(W,b)。同时，每个样本的y也是确定的常数，所以在损失函数L中唯一的变量就是模型的一堆参数C(W,b)。所以我们要选取一组参数，使得L达到最小，要怎么做呢？

我们可以这样，先随便给每一个参数定一个值，看看L的值是多少，然后再调整每个参数的值，在看看L是多少。。。。。。这样一直尝试了无数次以后，我们就能找到在所有参数取多少时，L的值能够达到最小了。

但是如果我们每一次都是毫无方向地胡乱调整每个参数的数值，那我们找到最小的L值都不知道要等到什么时候了，所以我们使用了一点点大学数学的知识。此处请大家记住以下结论：任何自变量在某处的值减去因变量对该自变量求偏导的值乘以一个正数，以此为自变量新的值带入函数后，计算出的新的因变量比原因变量小。

根据这个结论，我们可以使用一种叫做“梯度下降法”的方法，来在每一次中调整我们的各个参数的数值。下面，我们结合上文中所提到过的内容，给出一个直观的描述该方法的流程。

（六）训练神经网络的完整流程

1.构建神经网络，确定神经网络的超参数（即层数、每层的节点数、激活函数的形式）。

2.随机地给神经网络中的所有参数C(W,b)赋一组值。

3.依次输入每个样本的x值，根据当前神经网络的参数，计算并输出每个样本的y*值。

4.计算(sum((y-y*)^2))，并计算该函数对各参数当前的偏导值。

5.确定一个步长a，对网络中的每个参数w，计算w=w-a*(dL/dw)。

6.更新网络中所有参数。

7.重复3~6步，直到达到我们设定的最大循环次数。

此时网络中的这组参数C(W,b)，即为我们想要求得的，能取到min(sum((y-y*)^2))的那组参数。