Transformer 原理与代码解读(1)
目录
- 简介
- 为什么用Transformer
- RNN
- CNN
- Transformer
- Attention
- Transformer的图示
- query,keys和values以及输入序列的矩阵表示
- attention score的矩阵表示
- multihead self-attention
- Positional Embedding
- Transformer的整体结构
- Encoder
- Add & Norm
- Feed forward
- Decoder
- Masked Self-Attention
- Multi-head Attention
- Attention的可视化解释
- 小结
简介
自从2014年seq2seq被提出以来,encoder和decoder框架一直被广泛用于各类生成任务,其中最有代表性的就是机器翻译。而encoder和decoder所使用的基础模型也从最开始的RNN(LSTM), 逐步引入attention机制,到google提出Transformer, 完全利用self-attention来取代RNN。我们会在本文中阐述之前基于RNN的seq2seq,与Transformer的比较,并详细解读 Transformer的原理,之后我们会结合
Transformer的官方代码,详细分析其具体实现。
为什么用Transformer
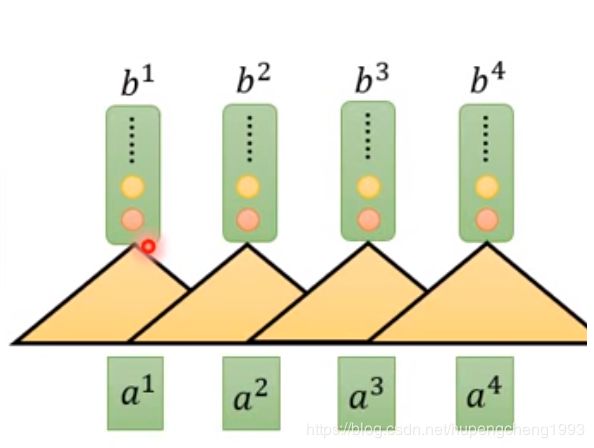
seq2seq中encoder和decoder,其本质就是将一个序列映射为另一个序列。我们可以选择不同的模型来实现这样的序列映射过程。假设我们的输入序列是 a 0 , a 1 , . . . , a n {a_0,a_1,...,a_n} a0,a1,...,an, 我们的输出序列是 b 0 , b 1 , … , b n {b_0, b_1, …, b_n} b0,b1,…,bn。
RNN
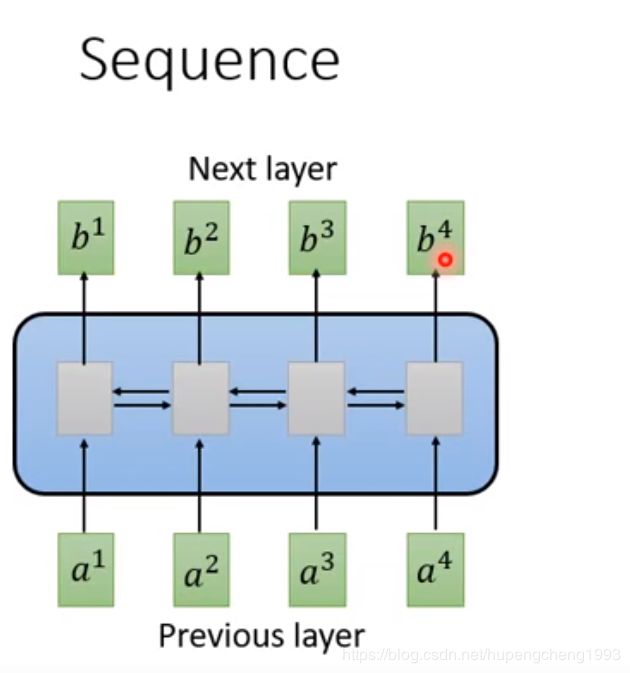
当我们选择使用RNN(各种不同的单向或者双向RNN)的时候,RNN的每个时间步的输出,不仅与其当前输入有关,也与其他时间步的输入有关,而且每个输出都需要在其之前的输出已经计算完成之后才能开始计算。这种方法的痛点在于序列的生成不能并行计算,另外就是由于RNN的记忆特性,对于long dependency的效果不够好。
CNN
对于RNN的序列生成不能并行计算的问题,我们可以使用CNN来解决。我们可以使用CNN将不同的连续输入映射成输出向量,即通过卷积核可以将某个时间步附近的输入映射成对应时间步的输出
但是由于卷积核的大小有限,这样做有一个问题在于每一个时间步的输出向量只能捕捉到该时间步附近的输入向量的信息,而不是全局的输入向量的信息,为了解决这个问题,我们可以用多层的CNN来学习全局输入信息
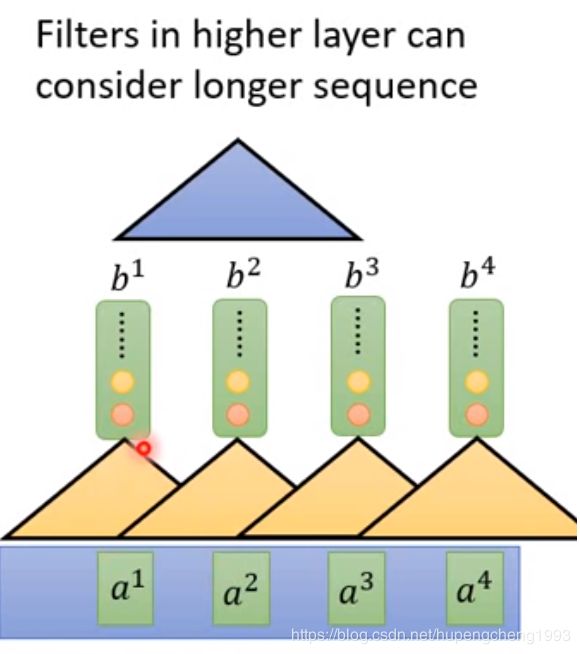
Transformer
我们可以看到对于序列生成来说,RNN的问题在于不能并行计算,而CNN的问题在于学习全局信息的时候需要的层数过深。针对这些问题,google创造性的提出了只用attention来实现序列生成,并解决了以上这些问题。在介绍transformer之前,我们首先来介绍一下attention机制
Attention
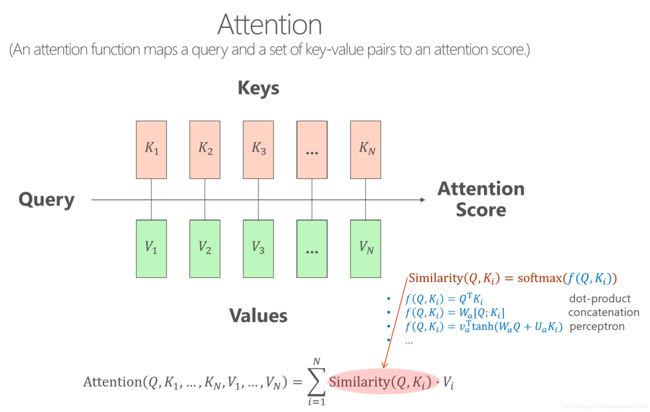
attention机制由三个部分组成,一个query,一组keys和一组values。其中query是单个向量,keys和values都是向量集合,attention的作用就是将query向量映射成一个新的向量,这个新的向量是由values这个集合中所有的向量加权得到的,而values集合中每个向量的加权系数是由query与keys集合中对应的向量计算得到的。这些加权系数的计算有多种不同的方式,比如dot-product, concatenation与perceptron等,而且所有的加权系数最后需要经过一个softmax函数,使得所有的加权系数之和为0.
下面两页截图引用自MSRA的Nan Duan博士在微软工程院所做的分享
Transformer的图示
在对attention机制有了基本了解之后,下面将介绍attention在Transformer中的应用。以下这些图示来自于台湾的李宏毅博士在YouTube上对于Transformer的介绍。
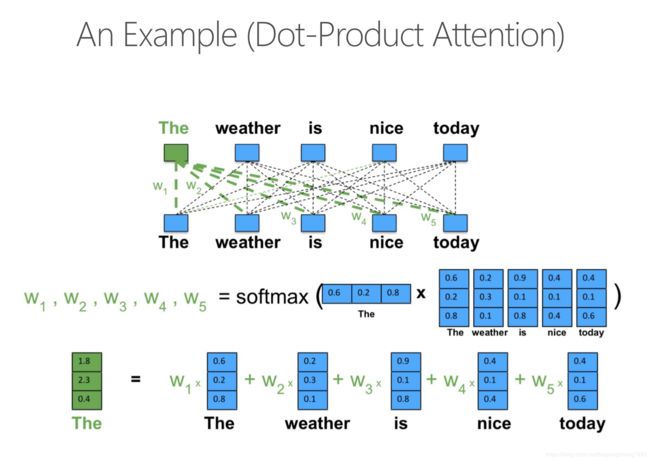
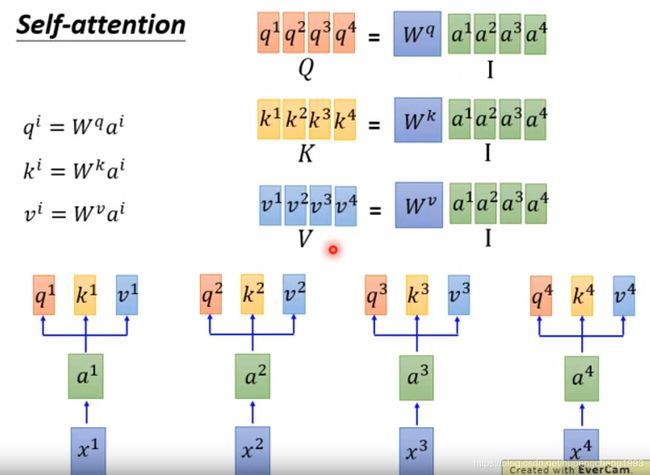
在Transformer的attention中,每个时间步的输入都通过一个矩阵映射成对应的query, key 和value
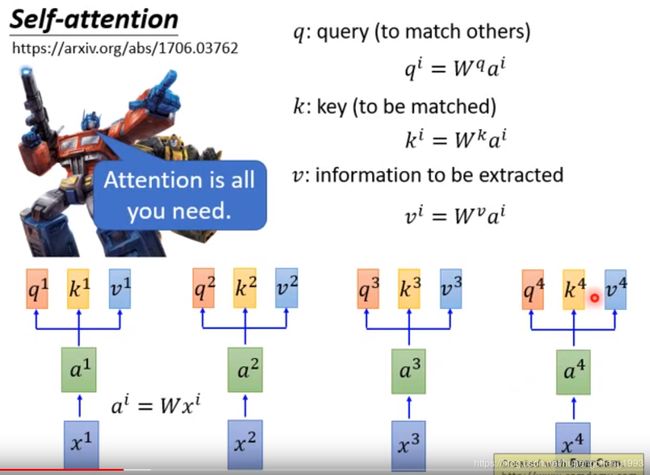
然后我们计算query对每一个key的attention score,注意transformer中使用的是dot-product, 由于query和key向量的维度会影响attention score(维度越大,dot-product的值越容易更大),因此将这些attention score除以 d 1 / 2 d^{1/2} d1/2
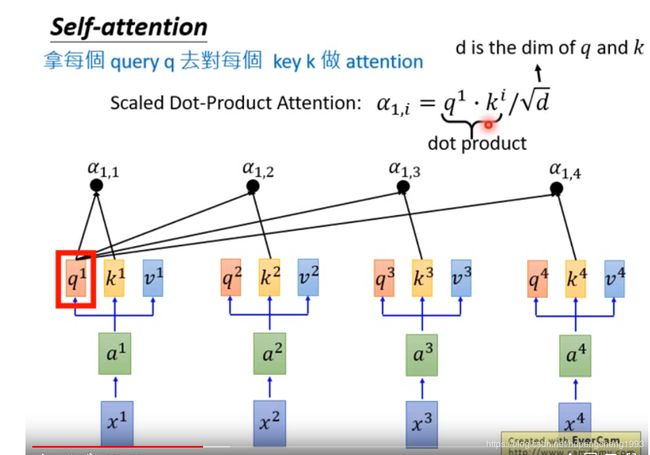
之后我们将query对所有keys的attention score做softmax,得到归一化的加权系数。这里要着重强调的是,由于softmax的特性,如果我们在做softmax之前对某个attention score上加上负无穷,那么经过softmax之后其对应的加权系数为0,也就是说values中的对应向量在最后的加权平均中不起作用。这种机制在代码实现的时候被用来处理需要被mask的向量,比如一个batch中的不同样本,其输入的长度是不一致的,为了方便计算我们会将所有的样本padding到相同的length,那么在经过attention模块的时候,我们就可以将对应的padding位置的attention score在经过softmax之前加上负无穷。
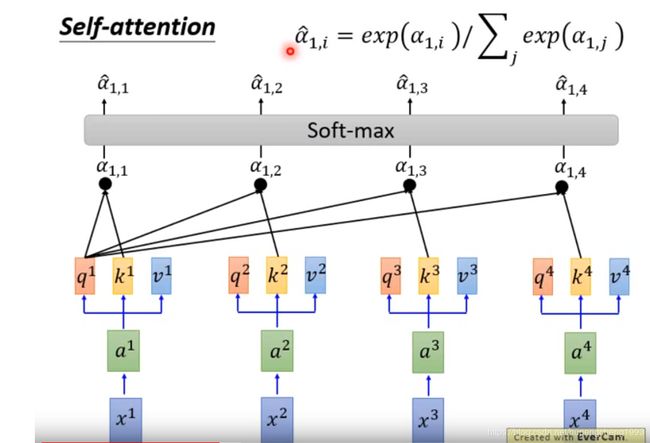
在得到了query相对于keys中各个向量的加权系数之后,我们就可以将values中的向量进行加权平均,得到该query对应时间步的输出

对其他的query进行同样的操作
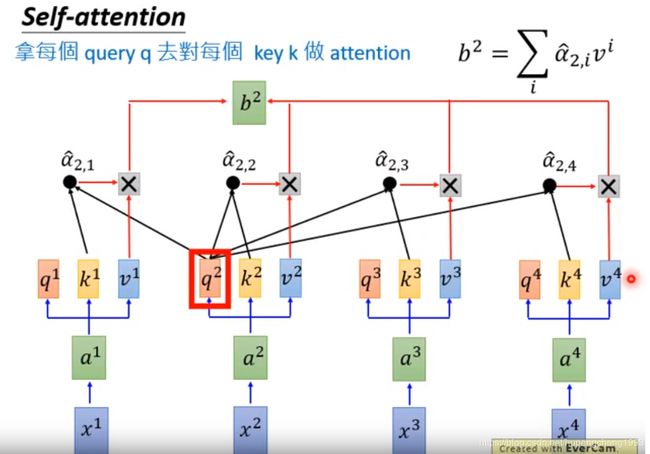 对于上述的每一个时间步的操作,我们将一种数学化的方式将这些操作合并成一个完整的矩阵操作
对于上述的每一个时间步的操作,我们将一种数学化的方式将这些操作合并成一个完整的矩阵操作
query,keys和values以及输入序列的矩阵表示
为了与图示保持一致,我们假设输入序列的长度为4,可以定义输入序列为
I = [ a 1 , a 2 , a 3 , a 4 ] I=[a^1,a^2,a^3,a^4] I=[a1,a2,a3,a4]
定义所有时间步的query为
Q = [ q 1 , q 2 , q 3 , q 4 ] Q = [q^1,q^2,q^3, q^4] Q=[q1,q2,q3,q4]
定义所有时间步的key为
K = [ k 1 , k 2 , k 3 , k 4 ] K=[k^1, k^2,k^3, k^4] K=[k1,k2,k3,k4]
定义所有时间步的value为
V = [ v 1 , v 2 , v 3 , v 4 ] V=[v^1,v^2,v^3,v^4] V=[v1,v2,v3,v4]
另外,query,key和value的映射矩阵分别为 W q W^q Wq, W k W^k Wk, W v W^v Wv
那么我们可以得到:
Q = [ q 1 , q 2 , q 3 , q 4 ] = W q [ a 1 , a 2 , a 3 , a 4 ] = W q I Q = [q^1,q^2,q^3, q^4] = W^q[a^1,a^2,a^3,a^4] = W^qI Q=[q1,q2,q3,q4]=Wq[a1,a2,a3,a4]=WqI
K = [ k 1 , k 2 , k 3 , k 4 ] = W k [ a 1 , a 2 , a 3 , a 4 ] = W k I K = [k^1,k^2,k^3, k^4] = W^k[a^1,a^2,a^3,a^4] = W^kI K=[k1,k2,k3,k4]=Wk[a1,a2,a3,a4]=WkI
V = [ v 1 , v 2 , v 3 , v 4 ] = W v [ a 1 , a 2 , a 3 , a 4 ] = W v I V = [v^1,v^2,v^3, v^4] = W^v[a^1,a^2,a^3,a^4] = W^vI V=[v1,v2,v3,v4]=Wv[a1,a2,a3,a4]=WvI
attention score的矩阵表示
我们将第 i i i个query相对于第 j j j的key算的的attention score表示成 α i , j \alpha_{i,j} αi,j,则 α i , j = k j T q i \alpha_{i,j} = k^{j^T} q^i αi,j=kjTqi
第 1 1 1个query相对于所有的key的attention score表示成
[ α 1 , 1 α 1 , 2 α 1 , 3 α 1 , 4 ] = [ k j T k j T k j T k j T ] q 1 \begin{bmatrix} \alpha_{1,1}\\ \alpha_{1,2}\\ \alpha_{1,3}\\ \alpha_{1,4} \end{bmatrix}= \begin{bmatrix} k^{j^T}\\ k^{j^T}\\ k^{j^T}\\ k^{j^T} \end{bmatrix} q^1 ⎣⎢⎢⎡α1,1α1,2α1,3α1,4⎦⎥⎥⎤=⎣⎢⎢⎢⎡kjTkjTkjTkjT⎦⎥⎥⎥⎤q1
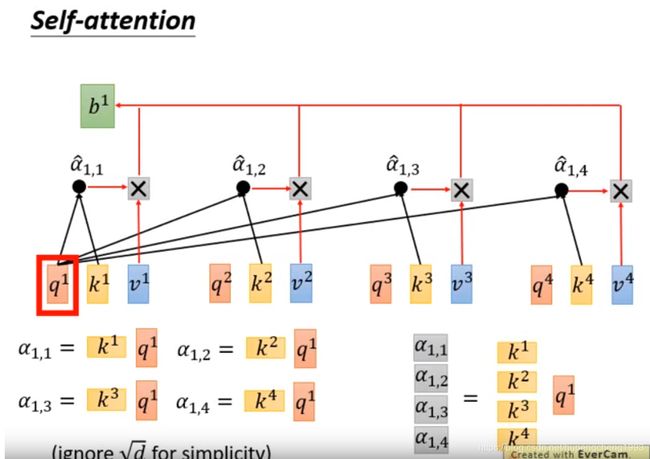
那么我们可以同样将所有的query相对于所有的keys的attention score表示成一个方阵 A A A, 其经过softmax之后的attention score表示成 A ^ \hat{A} A^
即
A ^ = s o f t m a x ( A ) = s o f t m a x ( K T Q ) \hat{A} = softmax(A) = softmax(K^TQ) A^=softmax(A)=softmax(KTQ)
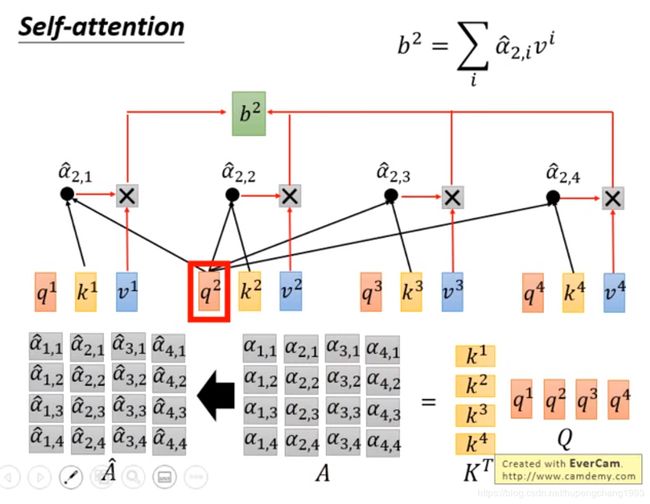 那么最终的输出 O O O可以表示成
那么最终的输出 O O O可以表示成
O = V A ^ O=V \hat{A} O=VA^
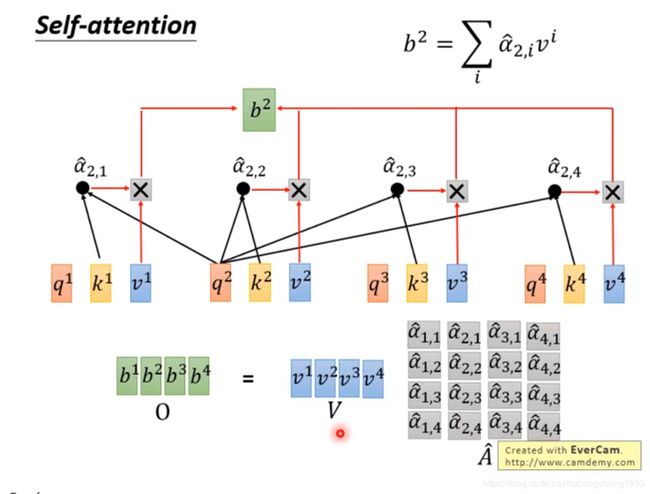
最后我们可以总结如下:
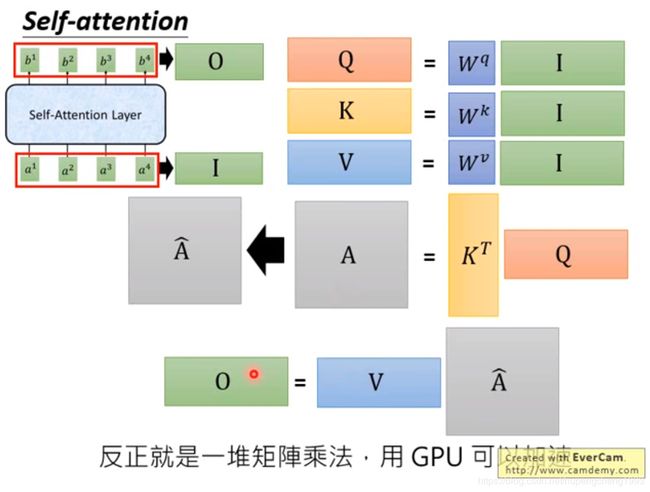
- 假设输入序列为 I I I, 其大小为 d ∗ l d*l d∗l,其中 d d d为 输入向量的大小, l l l为序列的长度
- W q , W k , W v W^q, W^k, W^v Wq,Wk,Wv的大小都为 d ∗ d d * d d∗d,则 Q , K , V Q, K, V Q,K,V的大小都为 d ∗ l d * l d∗l
- 所以输出的向量 O O O大小也为 d ∗ l d*l d∗l
multihead self-attention
在Transformer中还引入了一个新的概念,即multihead self-attention, 简单来说,就是有多个不同的attention,然后将所有attention head计算出来的向量concatenate到一起,形成一个size更大的向量。其关键在于每个head有不同的 W q W^q Wq, W k W^k Wk, W v W^v Wv.
Multihead self-attention的好处在于每个head都可以学习不同的信息,类似于CNN中多个卷积核。
对于一个attention head来说,其attention的方式和之前所述是一样的
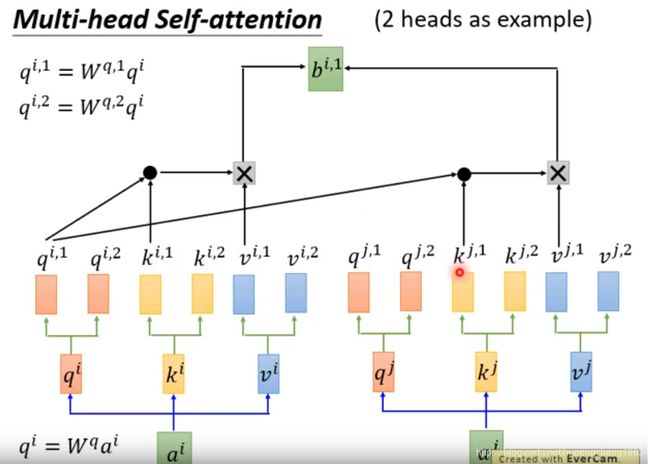 对于多个attention head, 我们将最终的输出序列concatenate起来即可
对于多个attention head, 我们将最终的输出序列concatenate起来即可
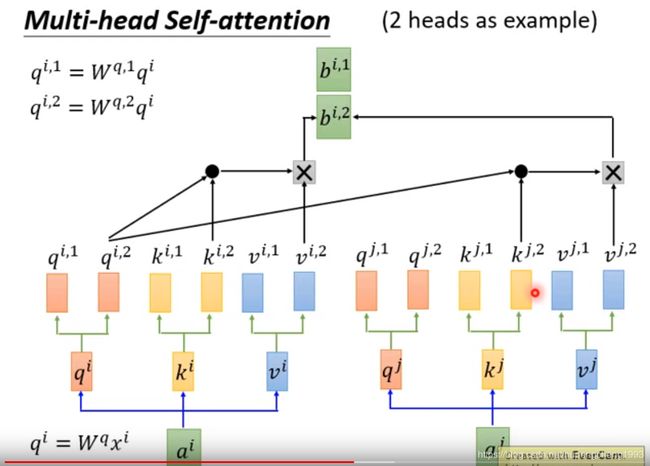 但是最后我们还是使用一个映射矩阵对concatenate起来的输出序列进行降维
但是最后我们还是使用一个映射矩阵对concatenate起来的输出序列进行降维
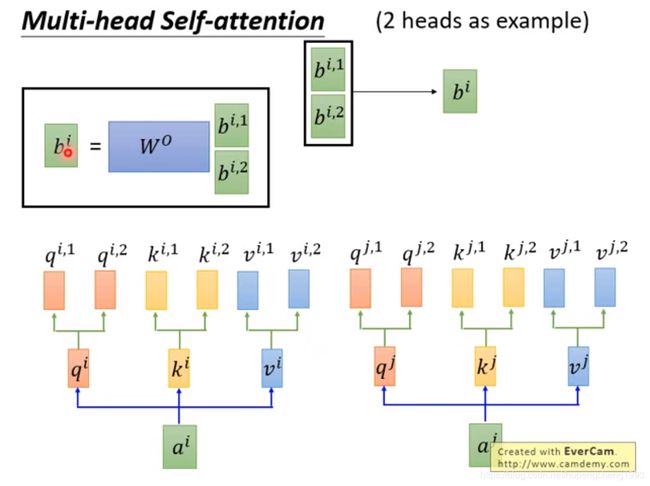
实际上对于multi head attention,我们可以用一个矩阵乘法来实现,我将在下一篇文章的代码解读中进行详细说明
Positional Embedding
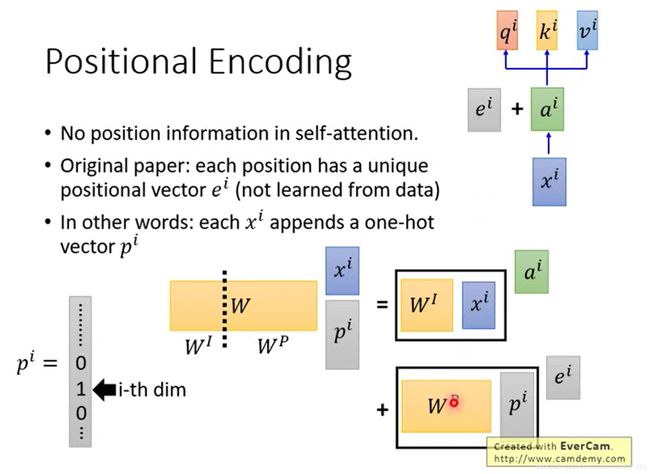
我们可以看到,对于每一个时间步的输出 b i b_i bi来说,其是通过对所有时间步的输入进行加权平均得到的,但是这里面并没有位置的信息,也就是说不管远近,其权重仅仅由q和k所算出来的系数决定
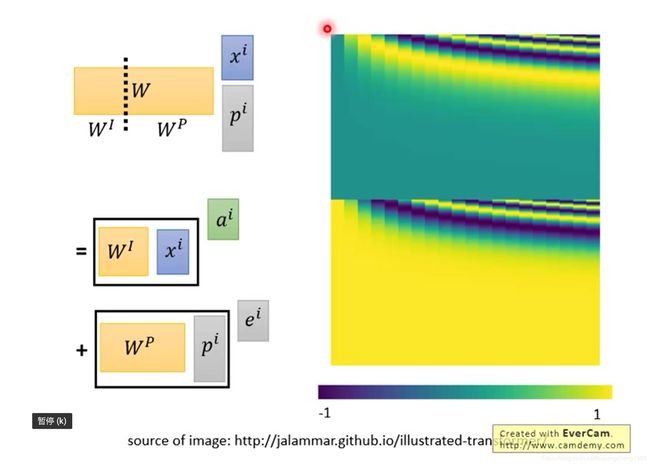
所以transformer中给每个原始输入加上了一个位置embedding,很多人可能会问,这个地方为什么是相加,而不是concatenate,这样位置向量中的信息是不是就被原始输入淹没了。其实我们可以这样来理解,我们将每个原始输入(不是每一层transformer的输入序列)和一个one hot的vector进行concatenate,然后和一个权重矩阵相乘,利用分块矩阵的知识,我们可以知道 e i e^i ei就相当于从矩阵 W P W^P WP中取得特定位置对应的位置vector。所以位置的信息可以理解成是以one hot的形式附加在原始输入上的。
需要注意的是,positional embedding 不是学出来的,而是人为设定的
Transformer的整体结构
下面这张图是transformer的整体结构,我们将结合这张图来详细说明Transformer是如何利用sefl-attention来实现encoder和decoder的
Encoder
对于左侧的encoder我们可以看到其最下面是原始输入,经过input embedding的变化并加上位置向量之后被送入多层的Attention 之中
在每一个所谓的attention layer中,最下面是multi-head的self-attention, 输出的向量序列和原始的输入向量序列做Add & Norm,然后再经过feed forward层。
Add & Norm
其中Add操作就是简单的将输入和输出相加,而norm是指layer normalization的操作,我们比较熟悉batch normalization,是将一个batch中所有相同的feature进行normalization,而layer normalization是指用对每一个样本的feature进行normalization,layer normalization被广泛用于seq2seq
Feed forward
Transformer中的feed forward网络可以理解为两个连续的线性变换,这两个变换中间是一个ReLU激活函数
F F N ( x ) = m a x ( 0 , x W 1 + b 1 ) W 2 + b 2 FFN(x) = max(0,xW_1 + b_1)W_2 + b_2 FFN(x)=max(0,xW1+b1)W2+b2
Decoder
对于decoder部分,首先是样本的输出(即当前样本的outputs,比如中翻英中的英文输出)变成输出向量,然后加上相应的位置向量,然后送入多层的attention layer中。
Masked Self-Attention
在decoder中的attention layer中有两个attention 部分,这两个attention都和encoder中的self-attention不同。首先输入序列进入到一个masked self-attention中,这是因为我们在prediction的时候decoder是从左往右地逐个predict,所以在我们做attention的时候,每一个时间步的输入应该只attention到之前的输入,因此我们要像前文所说的那样,通过在attention的系数矩阵的对应位置加上负无穷然后经过softmax函数,来将某些位置的权重mask掉。
Multi-head Attention
经过masked self-attention和一个Add & Norm操作之后的输出,被送到一个multi head attention中,注意这里不是self-attention,因为输入的query是decoder中的masked self-attention的输出,而key和value是encoder的输出。
经过多个attention layer之后的decoder输出,会经过一个线性层计算出每一个时间步的输出对应的概率。
Attention的可视化解释
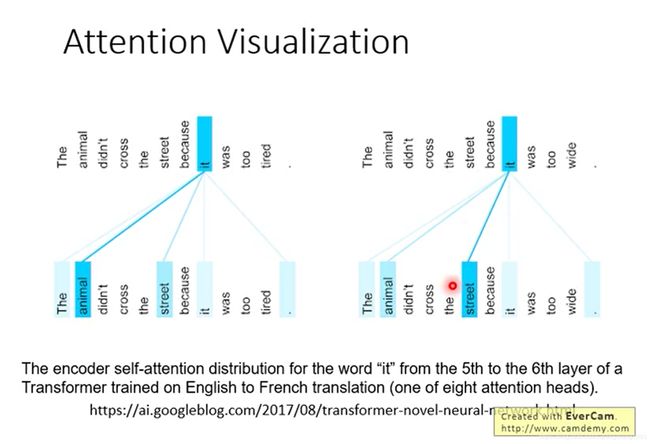
在介绍了Transformer的框架之后,我们再次来看一下该模型最基本的self-attention机制的可视化解释。在论文中,作者通过两个相似的句子中指示代词it对其所指示的名词的attention的结果
而对于multi-head attention能够学习不同维度的信息来说,作者也通过不同的head的attention情况来加以说明
小结
这篇文章主要描述了Attention, self-attention, multi-head attention, masked self-attention以及整体的transformer框架,对于google官方开源的Transformer代码我们将在下面一篇文章中进行介绍